Objetivos de aprendizaje
- Utilizar gráficos para analizar la cinética de una reacción.
Aprendiste que la ley de velocidad integrada para cada tipo común de reacción (zeroth, first, o second order in a single reactant) puede ser graficada como una línea recta. El uso de estas gráficas ofrece una alternativa a los métodos descritos para mostrar cómo cambia la concentración del reactivo con el tiempo y determinar el orden de la reacción. Ilustraremos el uso de estos gráficos considerando la descomposición térmica del gas NO2 a temperaturas elevadas, que ocurre según la siguiente reacción:
Los datos experimentales para esta reacción a 330°C se enumeran en la Tabla \(\PageIndex{1}); se proporcionan como , ln, y 1/ frente al tiempo para corresponder a las leyes de velocidad integradas para las reacciones de cero, primer y segundo orden, respectivamente.
| Tiempo (s) | (M) | ln | 1/ (M-1) |
|---|---|---|---|
| 1.00 × 10-2 | -4,605 | 100 | |
| 60 | 6.83 × 10-3 | -4,986 | 146 |
| 120 | 5.18 × 10-3 | -5,263 | 193 |
| 180 | 4.18 × 10-3 | -5,477 | 239 |
| 240 | 3.50 × 10-3 | -5.655 | 286 | 3,01 × 10-3 | -5.806 | 332 |
| 360 | 2,64 × 10-3 | -5.937 | 379 |
Las concentraciones reales de NO2 se representan en función del tiempo en la parte (a) de la Figura \(\PageIndex{1}\). Debido a que el gráfico de versus t no es una línea recta, sabemos que la reacción no es de orden cero en NO2. Un gráfico de ln frente a t (parte (b) en la Figura \(\PageIndex{1}\)) nos muestra que la reacción no es de primer orden en NO2 porque una reacción de primer orden daría una línea recta. Habiendo eliminado el comportamiento de orden cero y de primer orden, construimos un gráfico de 1/ frente a t (parte (c) en la Figura \(\PageIndex{1}\})). Este gráfico es una línea recta, indicando que la reacción es de segundo orden en NO2.
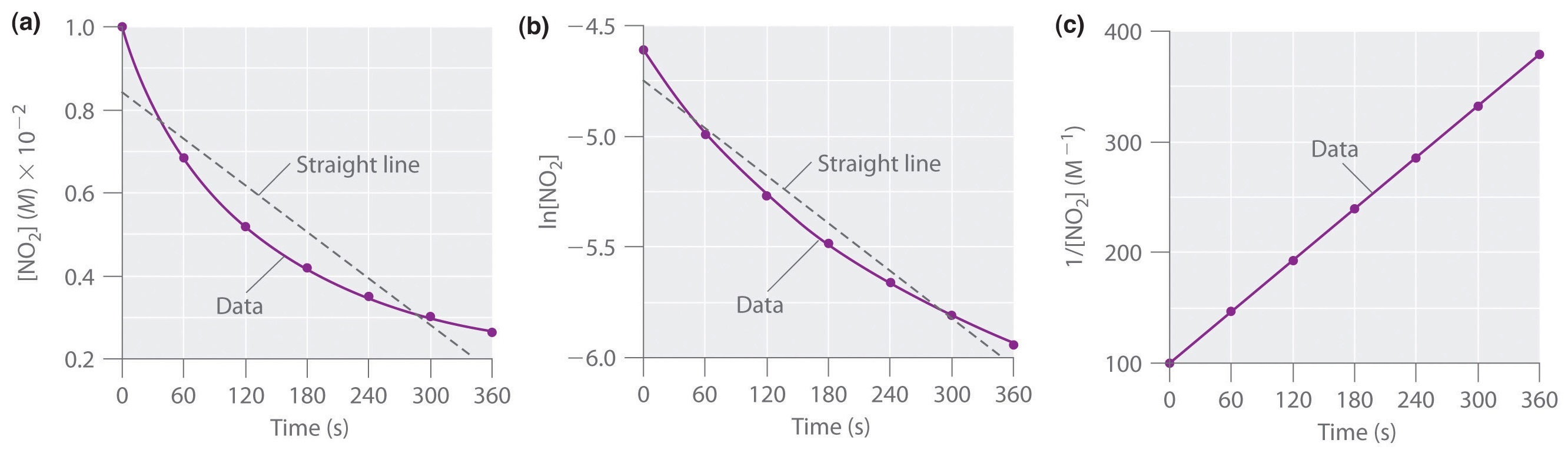
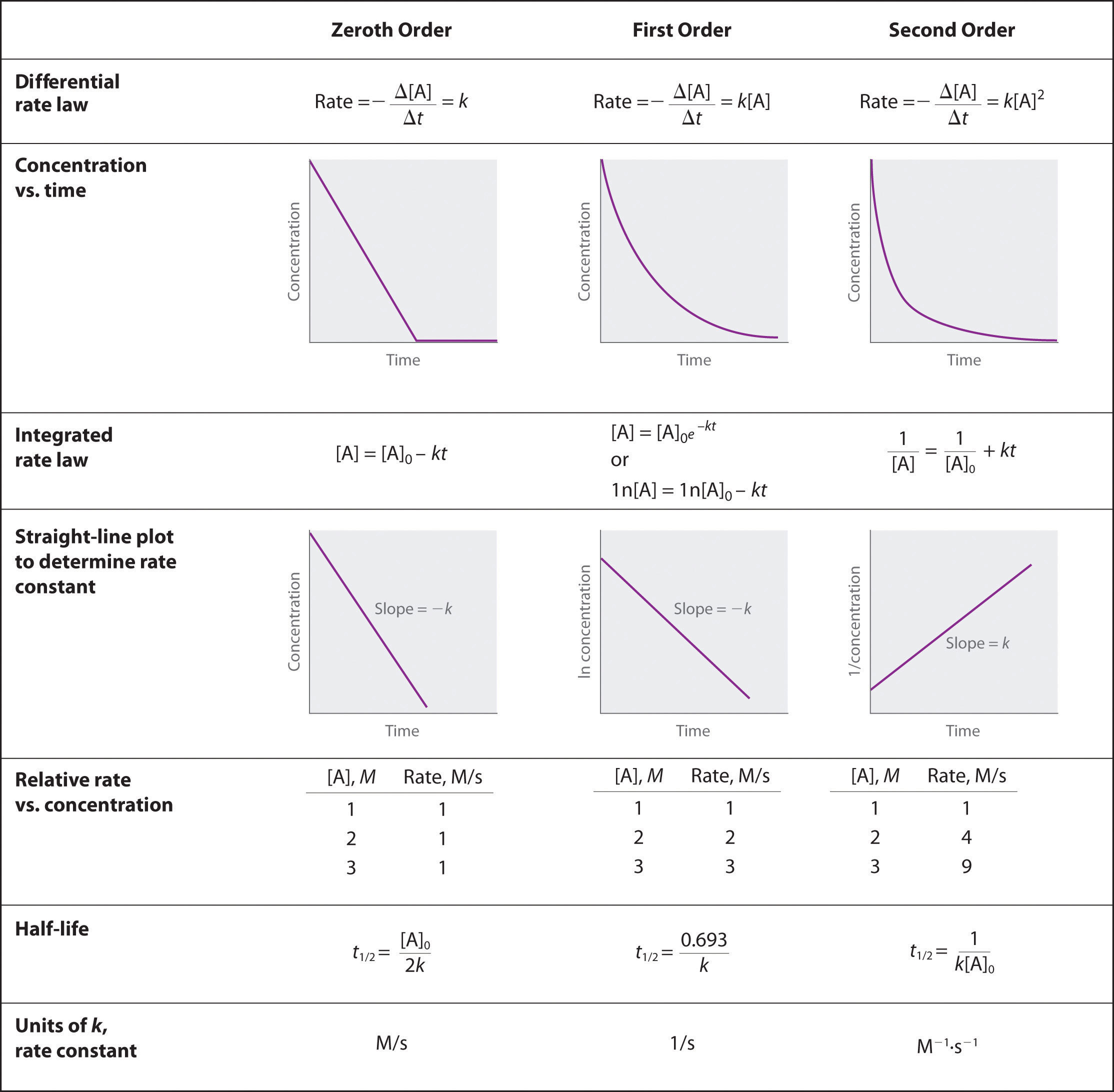
Acabamos de determinar el orden de reacción utilizando los datos de un único experimento mediante el trazado de la concentración del reactivo en función del tiempo. Debido a las formas características de las líneas que se muestran en la figura (índice de página 2), los gráficos pueden utilizarse para determinar el orden de reacción de una reacción desconocida. Por el contrario, el método de las tasas iniciales requería múltiples experimentos a diferentes concentraciones de NO2, así como tasas iniciales de reacción precisas, que pueden ser difíciles de obtener para las reacciones rápidas.
Ejemplo \(\PageIndex{1})
El pentóxido de nitrógeno (N2O5) se descompone en NO2 y O2 a temperaturas relativamente bajas en la siguiente reacción:
Esta reacción se lleva a cabo en una solución de CCl4 a 45°C. Las concentraciones de N2O5 en función del tiempo aparecen en la siguiente tabla, junto con los logaritmos naturales y las concentraciones recíprocas de N2O5. Trace una gráfica de la concentración en función de t, de la concentración ln en función de t y de 1/concentración en función de t y, a continuación, determine la ley de velocidad y calcule la constante de velocidad.
| Tiempo (s) | (M) | ln | 1/(M-1) |
|---|---|---|---|
| 0 | 0.0365 | -3.310 | 27,4 |
| 600 | 0.0274 | -3,597 | 36,5 |
| 1200 | 0.0206 | -3,882 | 48.5 | 1800 | 0,0157 | -4.154 | 63,7 |
| 2400 | 0.0117 | -4,448 | 85,5 |
| 3000 | 0.00860 | -4.756 | 116 |
| 3600 | 0,00640 | -5.051 | 156 |
Dado: Ecuación química equilibrada, tiempos de reacción y concentraciones
Se pide: gráfica de los datos, ley de velocidad y constante de velocidad
Estrategia:
A partir de los datos de la tabla, grafique por separado la concentración, el logaritmo natural de la concentración y el recíproco de la concentración (el eje vertical) frente al tiempo (el eje horizontal). Compare las gráficas con las de la Figura \N(\PageIndex{1}) para determinar el orden de la reacción.
B Escriba la ley de velocidad para la reacción. Utilizando los datos apropiados de la tabla y la gráfica lineal correspondiente a la ley de velocidad para la reacción, calcule la pendiente de la línea trazada para obtener la constante de velocidad para la reacción.
Solución
A continuación se presentan las gráficas de versus t, ln versus t, y 1/ versus t:
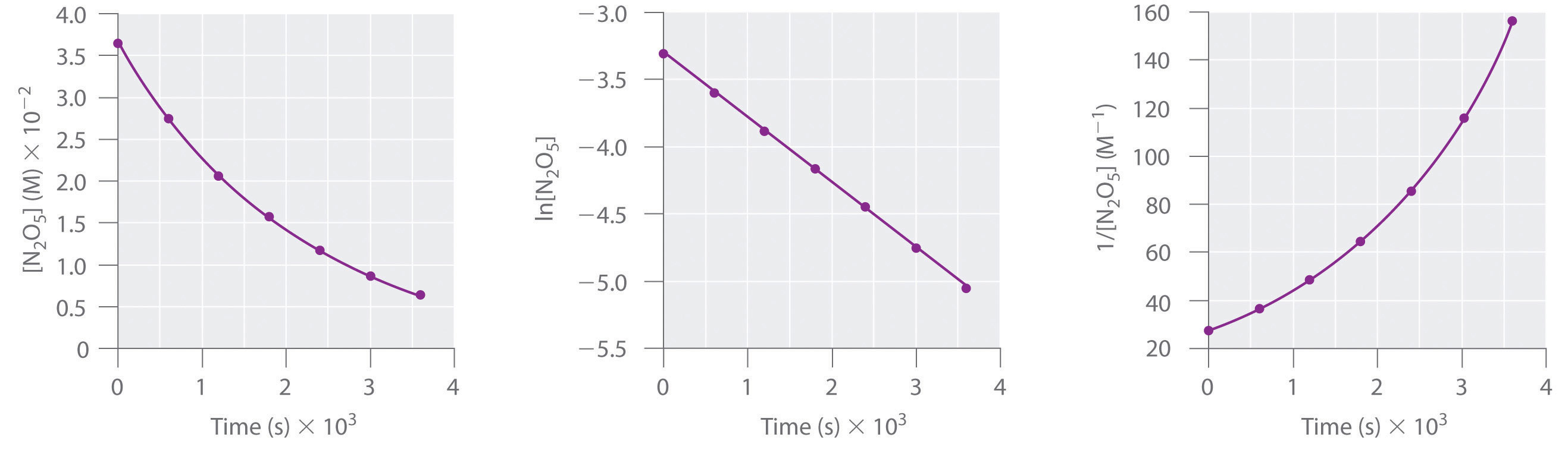
La gráfica de ln versus t da una línea recta, mientras que las gráficas de versus t y 1/ versus t no. Esto significa que la descomposición del N2O5 es de primer orden en .
B La ley de velocidad para la reacción es, por tanto,
tasa = k
Calcular la constante de velocidad es sencillo porque sabemos que la pendiente de la gráfica de ln frente a t para una reacción de primer orden es -k. Podemos calcular la pendiente utilizando dos puntos cualesquiera que se encuentren en la línea del gráfico de ln frente a t. Utilizando los puntos para t = 0 y 3000 s,
Por lo tanto, k = 4,820 × 10-4 s-1.
Ejercicio \(\PageIndex{1})
El 1,3-Butadieno (CH2=CH-CH=CH2; C4H6) es una molécula orgánica volátil y reactiva utilizada en la producción de caucho. Por encima de la temperatura ambiente, reacciona lentamente para formar productos. Las concentraciones de C4H6 en función del tiempo a 326°C se enumeran en la siguiente tabla junto con ln y las concentraciones recíprocas. Grafique los datos como concentración en función de t, concentración ln en función de t y 1/concentración en función de t. A continuación, determine el orden de reacción en el C4H6, la ley de velocidad y la constante de velocidad para la reacción.
| Tiempo (s) | ln | 1/ (M-1) | ||
|---|---|---|---|---|
| 0 | 1.72 × 10-2 | -4,063 | 58.1 | |
| 900 | 1,43 × 10-2 | -4,247 | 69.9 | 1800 | 1,23 × 10-2 | -4,398 | 81.3 |
| 3600 | -4.654 | 105 | ||
| 6000 | 7.30 × 10-3 | -4.920 | 137 |
Respuesta
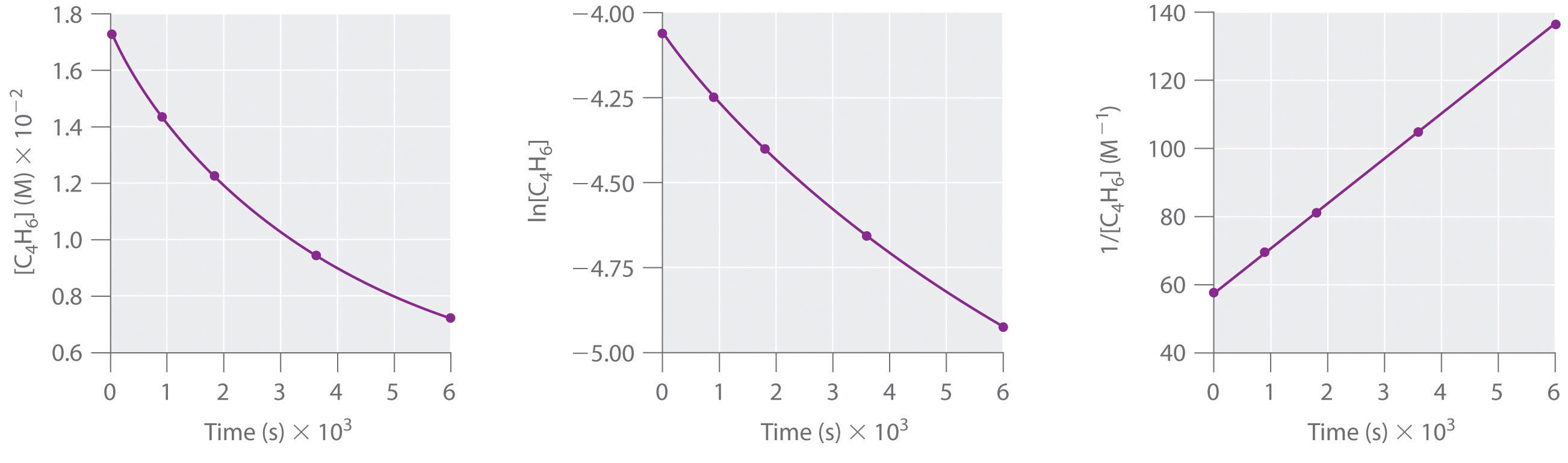
Segundo orden en C4H6; velocidad = k2; k = 1,3 × 10-2 M-1-s-1
Resumen
Para una reacción de orden cero, una gráfica de la concentración de cualquier reactivo frente al tiempo es una línea recta con una pendiente de -k. Para una reacción de primer orden, un gráfico del logaritmo natural de la concentración de un reactivo frente al tiempo es una línea recta con una pendiente de -k. Para una reacción de segundo orden, un gráfico de la inversa de la concentración de un reactivo frente al tiempo es una línea recta con una pendiente de k.