El análisis factorial es un procedimiento estadístico para describir las interrelaciones entre un número de variables observadas. El análisis factorial se utiliza para medir variables que no se pueden medir directamente, para resumir grandes cantidades de datos y para desarrollar y probar teorías. Existen dos grandes categorías de análisis factorial: exploratorio y confirmatorio. Las técnicas de análisis factorial exploratorio tienen una historia mucho más larga que las técnicas de análisis factorial confirmatorio. Las diferencias en los enfoques conducen a diferentes usos (por ejemplo, el desarrollo de la teoría frente a la confirmación de la teoría).
Propósitos
El análisis factorial tiene tres propósitos fundamentales. En primer lugar, es útil para medir constructos que no pueden observarse fácilmente en la naturaleza. Por ejemplo, no podemos oír, ver, oler, saborear o tocar la inteligencia, pero ésta puede inferirse a partir de la evaluación de variables observables, como el rendimiento en pruebas de habilidades específicas. El análisis factorial también es útil en el desarrollo de escalas para medir actitudes u otros constructos latentes de este tipo mediante la evaluación de las respuestas a preguntas específicas. En segundo lugar, el análisis factorial es útil para resumir una gran cantidad de observaciones en un número menor de factores. Por ejemplo, existen miles de descriptores de personalidad en el idioma inglés. Mediante el análisis factorial, los investigadores han podido reducir el número de factores distintos necesarios para describir la estructura de la personalidad. En tercer lugar, el análisis factorial es útil para aportar pruebas de validez de constructo (por ejemplo, validez factorial, convergente y discriminante). Por ejemplo, si ciertas variables observables están teóricamente relacionadas entre sí, el análisis factorial debería demostrar estas relaciones teóricas, demostrando simultáneamente que las mismas variables están razonablemente descorrelacionadas con las variables de otros factores latentes. Estos tres usos del análisis factorial pueden emplearse en el desarrollo y la comprobación de teorías psicológicas.
Modelo factorial básico
El problema del análisis factorial básico toma un número de variables observables y explica sus interrelaciones de forma análoga a una ecuación de regresión. El modelo factorial común es una ecuación de regresión en la que los factores comunes actúan como predictores de las variables X observadas. El modelo factorial básico se representa en la ecuación 1.
En esta ecuación, X es la matriz de variables observadas, L es la matriz de cargas factoriales o pesos de regresión, f es la matriz de factores comunes y u es la matriz de residuos. El objetivo es explicar las interrelaciones entre las variables X mediante los factores comunes, f, y los términos de error residuales, denominados unicidad. La varianza de X se divide en componentes comunes y específicos. Sin embargo, a diferencia de la regresión, los predictores, f, son desconocidos.
Para ofrecer un ejemplo ficticio de este problema, supongamos que se pide a una serie de supervisores que califiquen la relevancia de seis características de personalidad para el desempeño eficaz del trabajo por parte de los subordinados. Las características evaluadas son organizado, sistemático, descuidado, creativo,
intelectual e imaginativo. La tabla 1 muestra la matriz de correlación hipotética para estas variables. El problema del análisis factorial es explicar las relaciones entre estas variables con menos de seis factores latentes subyacentes. Organizado, sistemático y descuidado están correlacionados entre sí, pero no lo están con creativo, intelectual e imaginativo. Del mismo modo, creativo, intelectual e imaginativo están correlacionados entre sí, pero no lo están con organizado, sistemático y descuidado. Hay dos conjuntos de correlaciones que reflejan dos factores subyacentes.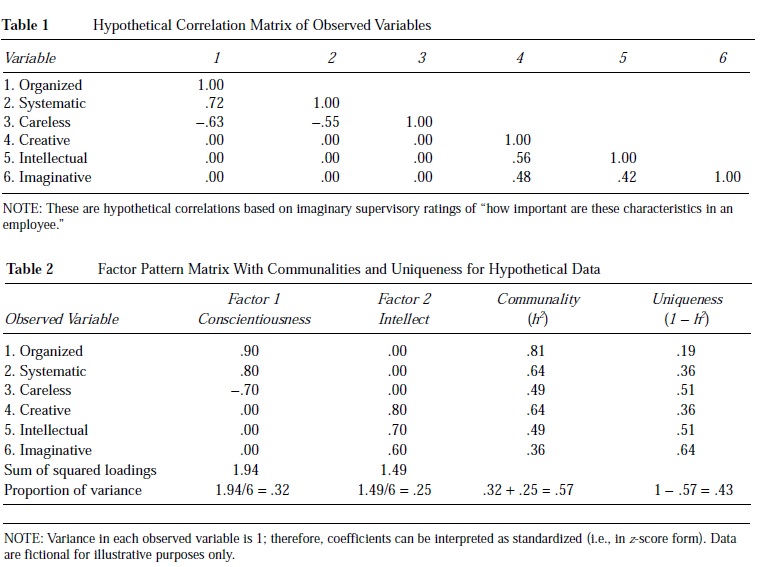
La Tabla 2 representa la matriz de patrones factoriales para estas variables y los correspondientes factores latentes. Los coeficientes del patrón en la Tabla 2 (columnas 2 y 3) son las correlaciones de las variables observadas con los factores. Diferentes matrices de patrones o de carga presentarán diferentes tipos de correlaciones (por ejemplo, correlaciones de Pearson, correlaciones parciales).
La comunalidad (h2) en la columna 4 de la Tabla 2 representa la varianza que la variable tiene en común con los factores que representa. La comunalidad es análoga a la correlación múltiple al cuadrado en la regresión. La unicidad en la columna 5 representa la varianza específica de una variable y no explicada por el factor. La unicidad es análoga a la varianza residual de la variable observada después de tener en cuenta los factores. Las seis variables ficticias representan dos factores inobservables, cada uno de los cuales explica entre el 36% y el 81% de la varianza de las variables observadas.
Además de la varianza asociada a las variables observadas, la solución del análisis factorial describe la varianza de los propios factores. La suma de las cargas cuadradas (SSL) de un conjunto de variables describe la varianza de cada factor. Antes de que se produzca cualquier transformación en las cargas factoriales, estas SSL se denominan valores propios. Lo ideal es que un número reducido de factores explique una gran parte de la varianza de las variables observadas. La tabla 2 muestra que los factores explican el 32% y el 25%, para un total del 57% de la varianza de las variables observadas. El 43% restante de la varianza de las variables observadas no es común a los factores.
Análisis factorial exploratorio
Típicamente, el objetivo del análisis factorial exploratorio (AFE) es dejar que los datos determinen las interrelaciones entre un conjunto de variables. Aunque un investigador que utiliza el AFE puede tener una teoría que relaciona las variables entre sí, hay relativamente pocas restricciones en el modelo factorial básico en un AFE. Este tipo de análisis ha sido útil en el desarrollo y debate de teorías durante más de un siglo.
El análisis factorial exploratorio es particularmente apropiado en las primeras etapas del desarrollo de la teoría y en las primeras etapas del desarrollo de escalas o pruebas. En primer lugar, el AFE es útil en la reducción de datos cuando las interrelaciones entre las variables no están especificadas de antemano. Un investigador que utiliza el EPT hace uso del razonamiento inductivo al tomar una serie de observaciones y desarrollar una teoría a partir de ellas. En el ejemplo de las características de los empleados de alto rendimiento, seis variables de personalidad se redujeron finalmente a dos factores. Así, para los análisis posteriores, sólo hay que analizar dos variables en lugar de las seis originales. La reducción de datos es particularmente útil para aliviar las preocupaciones de la multicolinealidad (correlaciones demasiado altas) entre un conjunto de predictores. Una segunda ventaja de la AFE es la capacidad de detectar un factor general. Cuando se analizan factorialmente varias pruebas específicas de capacidad cognitiva, tiende a surgir un factor general, junto con varios factores específicos. En la evaluación de la inteligencia, por ejemplo, todas las pruebas de capacidad se correlacionan en cierta medida con el factor general de la inteligencia, o g.
Por último, la AFE es particularmente útil en el desarrollo de escalas o pruebas porque permite al investigador determinar la dimensionalidad de la prueba y detectar cargas cruzadas (correlaciones de las variables con más de un factor). Las cargas cruzadas no suelen ser deseables. En el desarrollo de escalas, es ventajoso tener ítems que se relacionen con un solo factor. En el ejemplo anterior, las tres variables que representan la conciencia no tienen carga cruzada con el intelecto y viceversa.
Análisis factorial confirmatorio
El objetivo del análisis factorial confirmatorio (AFC) es poner a prueba las hipótesis derivadas de la teoría a partir de un conjunto de datos. El modelo factorial básico de la Ecuación 1 sigue siendo relevante, pero se imponen ciertas restricciones dado el modelo teórico particular que se está probando. Por ejemplo, a partir del ejemplo anterior, se podría utilizar el AFC para imponer restricciones al modelo factorial de forma que no se permitan cargas cruzadas. Desarrollado durante la década de 1960, el AFC es un desarrollo estadístico más reciente que el AFE (desarrollado en 1904).
El análisis factorial confirmatorio es particularmente útil en un proceso de razonamiento deductivo. La comprobación de hipótesis específicas es posible cuando se utiliza el AFC. Por ejemplo, un investigador puede abordar la significación estadística de las cargas factoriales individuales. En el ejemplo anterior, dada la correlación relativamente pequeña, se podría determinar con certeza estadística el grado en que la variable observada, imaginativa, está correlacionada con el factor latente, intelecto.
Con el AFC, es posible probar la hipótesis de que dos factores frente a un solo factor (o cualquier otra combinación numérica) subyacen a un conjunto de datos. En el AFE, los investigadores se basan en reglas empíricas y en la intuición, que pueden llevar al investigador por el mal camino, pero en el AFC, los modelos pueden compararse explícitamente mediante pruebas estadísticas de hipótesis nulas. Otro uso del AFC es evaluar la equivalencia de partes del modelo factorial básico dentro de un conjunto de datos determinado. Por ejemplo, se podría hipotetizar que todas las variables observadas para el intelecto están igualmente relacionadas con el intelecto. Con el AFC, la equivalencia de estas relaciones puede comprobarse imponiendo restricciones a las cargas del modelo factorial básico (es decir, L en la ecuación 1).
También es importante determinar si los resultados de un análisis factorial son similares entre grupos demográficos. El análisis factorial confirmatorio permite realizar pruebas de invariancia -es decir, la equivalencia de la estructura factorial, las cargas, la unicidad- entre diferentes grupos (por ejemplo, étnicos, de género, culturales) de individuos. Un investigador puede estar interesado en saber si surgiría la misma estructura factorial hipotética si se comparan las respuestas de los supervisores de los trabajadores de la industria con las de los supervisores de los trabajadores de los servicios. Puede darse el caso de que la variable observada no se relacione con los factores latentes de la misma manera para los dos grupos. Por ejemplo, el indicador sistemático observado puede estar menos relacionado con el factor conciencia para los trabajadores de servicios que para los trabajadores de la industria. En un AFC que está probando la equivalencia de las cargas factoriales, un investigador puede probar la hipótesis de que las correlaciones de los dos grupos son iguales o diferentes.
El análisis factorial confirmatorio tiene una mayor flexibilidad de control que el AFE. Con el AFC, algunos factores pueden especificarse como oblicuos (correlacionados entre sí), mientras que otros se especifican como ortogonales (no correlacionados entre sí). Dentro de un mismo AFE, los factores se interpretan como oblicuos u ortogonales, pero no como una combinación de ambos. Además, el AFC permite al investigador imponer con flexibilidad restricciones adicionales sujetas a la teoría (por ejemplo, permitir la unicidad correlativa). Sin embargo, una de las ventajas del AFE es que no se necesitan tales restricciones o especificaciones teóricas. Por lo tanto, si no existe ninguna, entonces EFA puede ser una mejor opción.
- Gorsuch, R. L. (2003). El análisis factorial. En J. A. Schinka & W. F. Velicer (Eds.), Handbook of psychology: Métodos de investigación en psicología (Vol. 2, pp. 143-164). Hoboken, NJ: Wiley.
- Hurley, A. E., Scandura, T. A., Schriesheim, C. A., Brannick, M. T., Seers, A., Vandenberg, R. J., & Williams, L. J. (1997). Análisis factorial exploratorio y confirmatorio: Pautas, problemas y alternativas. Journal of Organizational Behavior, 18, 667-683.
- Lance, C. E., & Vandenberg, R. J. (2002). Análisis factorial confirmatorio. En F. Drasgow & N. Schmitt (Eds.), Measuring and analyzing behavior in organizations: Avances en medición y análisis de datos (pp. 221254). San Francisco: Jossey-Bass.
- Preacher, K. J., & MacCallum, R. C. (2003). Reparando la máquina de análisis de factores eléctricos de Tom Swift. Understanding Statistics, 2, 13-43.
- Thompson, B. (2004). Análisis factorial exploratorio y confirmatorio: Comprensión de conceptos y aplicaciones. Washington, DC: American Psychological Association.
- Vandenberg, R. J., & Lance, C. E. (2000). Una revisión y síntesis de la literatura sobre invariabilidad de la medición: Sugerencias, prácticas y recomendaciones para la investigación organizativa. Organizational Research Methods, 3, 4-69.