La cuarta dimensión es un lugar al que se puede viajar yendo en una dirección perpendicular a la tercera dimensión. Para el ojo inexperto, esta afirmación no tiene ningún sentido. ¿Cómo puede haber una dirección perpendicular a un espacio tridimensional? Para entender mejor este concepto, tenemos que recorrer poco a poco todas las dimensiones y analizar qué cambios se producen entre cada una de ellas.

Dimensión zerótica
La dimensión zerótica es una en la que no solemos pensar. Los puntos son los únicos seres dimensionales que se pueden entender correctamente en la dimensión zeroth. No tienen absolutamente ninguna dimensión, ni anchura, ni longitud, ni altura. Son lo más pequeño que pueden ser, pero también lo más grande que pueden ser al mismo tiempo.
Cuando buscamos profundizar en nuestra comprensión de la cuarta dimensión. Podemos examinar un cubo en cada dimensión mientras progresamos. Un cubo en la dimensión cero sería simplemente un punto. Todas sus dimensiones son iguales en todas las direcciones porque no hay ninguna. El cubo sigue representando un punto en el espacio, pero hasta ahí llega su poder en la dimensión cero. Ahora, pasemos a la 1-D.
Primera dimensión
La transición entre la dimensión zeroth y la primera dimensión implica una extrusión en cualquier dirección. En la primera dimensión, todo existe como una línea. Lo único que difiere entre los objetos de la primera dimensión es su longitud. Las líneas tienen todas la misma anchura y la misma altura, pero su longitud puede ser variada.
Si quieres hacer líneas de distinto grosor, entonces tienes que pasar a las líneas bidimensionales. Un cubo en la primera dimensión se vería como una línea con la misma longitud que dicho cubo, pero sin valores de anchura o altura.
Segunda dimensión
Transformar un segmento de línea en una dirección perpendicular a la dirección de 1 dimensión te lleva a la segunda dimensión. Mantén esta idea en mente a medida que ampliamos nuestro conocimiento dimensional y observa que esta acción perpendicular se repite a medida que nos movemos a través de las dimensiones.
En la segunda dimensión, nuestro cubo puede empezar a parecerse a un cubo, pero apenas. Un cubo existiría como un cuadrado en la segunda dimensión. Se puede, por supuesto, dibujar una representación de un cubo 3D en 2 dimensiones, pero eso no es lo que sería un cubo en 2 dimensiones. Más bien se trataría simplemente de una representación de la tercera dimensión superpuesta a la segunda.
La longitud y la anchura pueden variar en la segunda dimensión, lo que permite obtener formas y geometría básicas. Cuando pasamos a la tercera dimensión, las matemáticas empiezan a ser más complejas.
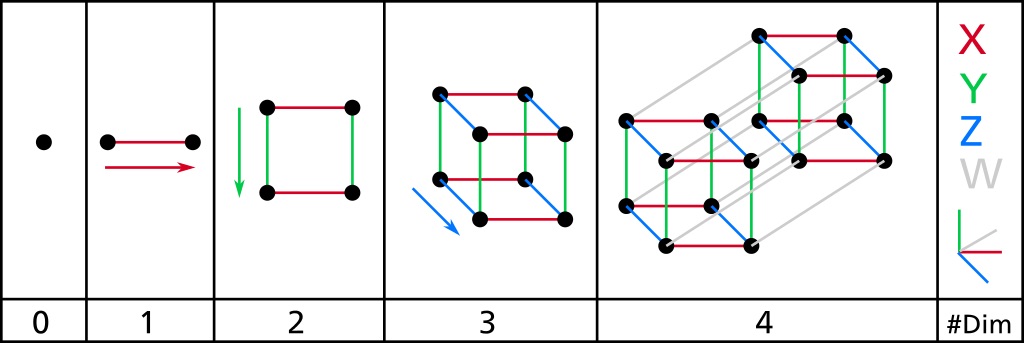
Tercera dimensión
El cubo de la segunda dimensión se extruye ahora en una tercera dirección perpendicular a ambos lados del cuadrado 2D. Para poner esto en términos cartesianos, el cuadrado 2D existía en las direcciones X e Y. Al pasar a la tercera dimensión se extruye ese cuadrado en la dirección Z. En la tercera dimensión es donde nuestro cubo se convierte realmente en un cubo en nuestro sentido tradicional. El objeto tiene dimensiones de anchura, longitud y altura.
A lo largo de todas las dimensiones, es importante señalar que un cubo mantendrá todas sus propiedades básicas en teoría. Todos los ángulos serán rectos y todos los lados serán iguales. Introduciendo otro principio de dimensiones, podemos examinar qué ocurriría si el cubo se expandiera indefinidamente. Cuando un cubo en la tercera dimensión se expande hasta el infinito, abarca la totalidad del espacio de 3 dimensiones.
Hasta aquí, probablemente deberías comprender estas 3 dimensiones, después de todo, son las dimensiones con las que más comúnmente nos asociamos.
Cuarta dimensión
Cuando llevamos el cubo a la cuarta dimensión, empezamos a experimentar algunas matemáticas contraintuitivas. Extruimos el cubo en una dirección perpendicular a todas las tres primeras. Esto es imposible dentro de la tercera dimensión porque sólo hay 3 dimensiones en las que el cubo ya está expandido. Cuando añadimos la cuarta dimensión, para mantener las propiedades del cubo de que todos los ángulos sean de 90 grados y todas las caras sean iguales, debemos extruir en esta nueva dimensión.
Los cubos en las cuartas dimensiones se llaman técnicamente teseractos. Los objetos en 4D difieren en longitud, anchura, altura y longitud. La superposición de la longitud en cualquiera de las dimensiones anteriores da a un objeto en las dimensiones posteriores una longitud de 0, o un valor infinitamente pequeño.
Todas las aristas de un teseracto son iguales, y todos los ángulos son rectos. Esto tiene sentido en teoría, pero cuando empezamos a imaginar cómo sería un teseracto, estamos limitados por nuestras mentes tridimensionales. Para ver un teseracto, tenemos que superponer este objeto de cuarta dimensión en la tercera dimensión.
La principal forma en que representamos un teseracto, o cubo de cuarta dimensión, es proyectándolo en la tercera dimensión con perspectiva. Esta representación puede verse a continuación.
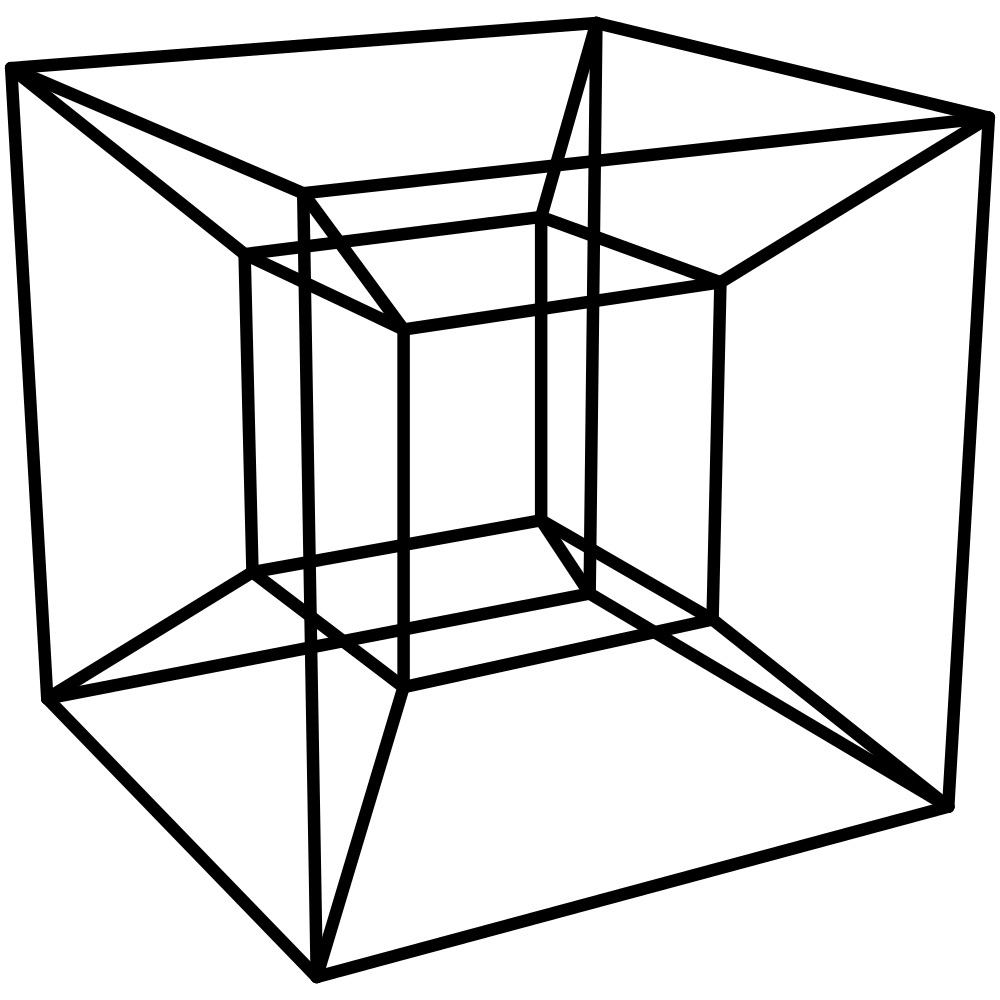
Esta es también una representación en perspectiva de un teseracto en forma de gif.

Esta representación no es el aspecto de un cubo en 4D, es simplemente el aspecto de uno en perspectiva visto desde la tercera dimensión. Para resumir nuestra comprensión de la cuarta dimensión, los objetos en 4D varían en valor por la longitud, la anchura, la altura y la longitud. Todas estas medidas dimensionales se extienden en una dirección perpendicular a las tres anteriores. La anchura es perpendicular a la longitud, la altura es perpendicular a la anchura y a la longitud y, por último, la longitud es perpendicular a la altura, a la longitud y a la anchura.
Estos conceptos son difíciles de entender pero, con suerte, esto te da una buena visión general de cómo funciona la cuarta dimensión y cómo la interpretamos desde nuestros ojos tridimensionales.
¿Todavía no tiene sentido? Deja que Carl Sagan te lo explique.