La ecuación de Schrödinger, a veces llamada ecuación de onda de Schrödinger, es una ecuación diferencial parcial.Utiliza el concepto de conservación de la energía (energía cinética + energía potencial = energía total) para obtener información sobre el comportamiento de un electrón unido a un núcleo.Lo hace permitiendo calcular la función de onda de un electrón, Ψ.

Resolviendo la ecuación de Schrödinger obtenemos Ψ y Ψ2.Con ellas obtenemos los números cuánticos y las formas y orientaciones de los orbitales que caracterizan a los electrones en un átomo o molécula.
La ecuación de Schrödinger da soluciones exactas sólo para núcleos con un electrón: H, He+, Li2+, Be3+, B4+, C5+, etc.En lenguaje matemático, decimos que las soluciones analíticas para Ψ son posibles sólo para sistemas de un electrón.Los sistemas de un solo electrón se describen a menudo como hidrogénicos -lo que significa «como el hidrógeno»
Para todos los demás átomos, iones y moléculas, no son posibles soluciones analíticas para Ψ; se utilizan entonces métodos de cálculo por aproximación, como la aproximación orbital y el teorema de la variación.
Existe una ecuación de Schrödinger dependiente del tiempo y una ecuación de Schrödinger independiente del tiempo.
La ecuación independiente del tiempo considera que el estado cuántico del electrón no cambia, por lo que considera al electrón como una onda estacionaria.La ecuación independiente del tiempo permite encontrar las densidades de los electrones (es decir, los tamaños y formas de los orbitales atómicos y moleculares) utilizando Ψ2, el cuadrado de la función de onda.
Los orbitales p de abajo son ejemplos de Ψ2:



La ecuación deIndependent Schrödinger Equation
La ecuación de Schrödinger independiente del tiempo puede expresarse en una taquigrafía matemática muy comprimida como:
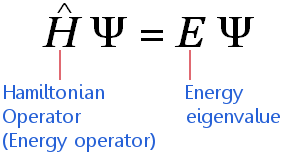
La ecuación se aplica a los electrones que viajan a velocidades no relativistas. (Esto significa que requiere ajustes antes de que pueda aplicarse a elementos de gran masa.)La ecuación dice:
La ecuación independiente del tiempo puede escribirse en cualquier sistema de coordenadas adecuado, como las coordenadas cartesianas (x,y,z).Para los átomos de hidrógeno, las coordenadas polares esféricas son más adecuadas, por lo tanto:
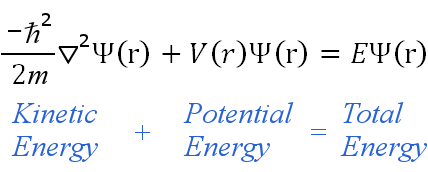
Las restricciones dan lugar a la cuantización
La ecuación se resuelve para encontrar Ψ.Las restricciones impuestas en la resolución de la ecuación producen cuantificación – es decir, las soluciones encontradas para Ψ están restringidas a ciertos valores y todos los demás valores están prohibidos.
Estas restricciones son:
– Ψ y su primera derivada parcial deben ser continuos.
– Ψ debe ser normalizable: esto significa que hay un 100% de probabilidad de que el electrón se encuentre en algún lugar del universo.Para un valor real de Ψ, la normalización requiere que:
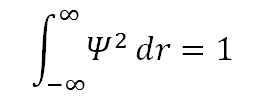
– A medida que aumenta la distancia al núcleo, el electrón se desprende y deja de estar ligado.Es decir, a medida que r → ∞, H → H+ + e-.
La función de onda produce números cuánticos
La función de onda del electrón existe en tres dimensiones, por lo que las soluciones de la ecuación de Schrödinger tienen tres partes.Estas se obtienen explícitamente mediante un método de resolución de ecuaciones diferenciales parciales llamado separación de variables. Haciendo esto, obtenemos:
Resulta que las soluciones para Ψ sólo son posibles cuando:
– En R(r), una constante, llámese n, tiene valores 1, 2, 3, 4,….
– En P(θ), una constante, llamada l, tiene los valores 0, 1, 2, 3,…(n-1)
– En F(φ), una constante, llamada ml, tiene los valores -l, (l+1),…0.., (l+1), l
Y así a partir de la función de onda Ψ la ecuación de Schrödinger ha entregado los tres números cuánticos que caracterizan el comportamiento del electrón en un átomo.
– n: el número cuántico principal
– l: el número cuántico del momento angular orbital
– ml: el número cuántico magnético
La función de onda produce formas y tamaños orbitales
Ψ2, la densidad de probabilidad, define las formas y tamaños de los orbitales de los electrones.
