¿Has notado alguna vez gráficos que se parecen, pero uno está más estirado verticalmente que el otro? Todo esto es gracias a la técnica de transformación que llamamos estiramiento vertical.
El estiramiento vertical en una gráfica tirará de la gráfica original hacia fuera en un factor de escala determinado.
Cuando una función base se multiplica por un determinado factor, podemos graficar inmediatamente la nueva función aplicando el estiramiento vertical.
Antes de profundizar en esta técnica de transformación, lo mejor es que repases tus conocimientos sobre los siguientes temas:
- Entender las funciones madre más comunes que podemos encontrar.
- Refrescar tus conocimientos sobre las transformaciones verticales y horizontales.
- Asegúrate de que los valores de x siguen siendo los mismos, por lo que la base de la curva no cambiará.
- Esto significa que al aplicar estiramientos verticales sobre una gráfica base, sus intersecciones x seguirán siendo las mismas.
- Toma nota de los nuevos puntos críticos, como el nuevo punto máximo de la gráfica.
- Un estiramiento vertical ocurre sólo cuando el factor de escala es mayor que 1.
- Asegúrate de multiplicar las coordenadas y por el mismo factor de escala.
- Mantén la posición de las intersecciones x.
- La función estirada verticalmente tendrá el mismo dominio y un nuevo rango.
No dudes en hacer clic en los enlaces para refrescar tus conocimientos sobre estos temas esenciales. Ahora hablaremos de la tercera técnica de transformación: el estiramiento vertical.
¿Qué es un estiramiento vertical?
El estiramiento vertical se produce cuando una gráfica base se multiplica por un determinado factor que es mayor que 1. Esto hace que la gráfica sea arrastrada hacia fuera pero conservando los valores de entrada (o x). Cuando una función se estira verticalmente, esperamos que los valores y de su gráfica se alejen del eje x.
El gráfico siguiente muestra la gráfica de f(x) y sus transformaciones. ¿Por qué no observamos cómo se transforma f(x) cuando multiplicamos los valores de salida por un factor de 3 y 6?
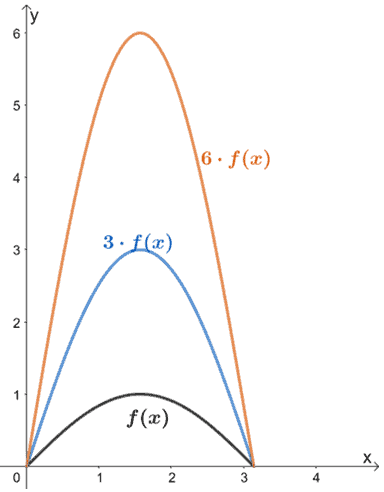
Cuando f(x) se multiplica por factores de escala de 3 y 6, su gráfica se estira por los mismos factores de escala. También podemos ver que sus valores de entrada (x para este caso) siguen siendo los mismos; sólo los valores de y se vieron afectados cuando estiramos f(x) verticalmente.
¿Cómo generalizamos esta regla? Cuando tenemos |a| > 1, a – f(x) estirará la función base en un factor de escala de a. Los valores de entrada seguirán siendo los mismos, por lo que los puntos de coordenadas de la gráfica serán ahora (x, ay).
Esto significa que si f(x) = 5x + 1 se estira verticalmente en un factor de 5, la nueva función será equivalente a 5 – f(x). Por lo tanto, la función resultante es 5(5x + 1) = 25x + 5.
¿Cómo estirar verticalmente una función?
Cuando se da la gráfica de una función, podemos estirarla verticalmente tirando de la curva hacia fuera en función del factor de escala dado. Aquí hay algunas cosas que hay que recordar cuando estiramos verticalmente las funciones:
¿Por qué no probamos a estirar verticalmente la función y = √x en un factor 2?
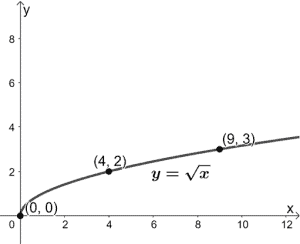
Hemos incluido algunos puntos guía destacando cómo también cambian cuando graficamos la nueva función y = 2√x. Qué esperamos de la nueva gráfica?
Seguirá empezando en el origen, las coordenadas y aumentarán en un factor de 2 y la gráfica se estirará en un factor de 2.
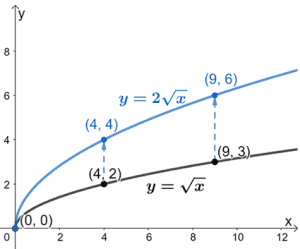
La gráfica anterior muestra cómo podemos estirar verticalmente la gráfica de y =√x por un factor de 2 para graficar también y = 2√x.
Podemos aplicar el mismo proceso al estirar verticalmente diferentes tipos de funciones y gráficas. Antes de probar otros ejemplos, ¿por qué no resumimos lo que hemos aprendido hasta ahora sobre el estiramiento vertical?
Resumen de la definición y propiedades del estiramiento vertical
Ahora hemos aprendido sobre el efecto de escalar una función por un factor positivo, a. A continuación, hay algunas indicaciones importantes que debemos recordar cuando tratamos con estiramientos verticales en gráficas:
Tengamos en cuenta estos útiles recordatorios cuando resolvamos las preguntas después de esta sección. ¿Preparados? Empecemos a aplicar esta técnica de transformación!
Ejemplo 1
La función, g(x), se obtiene estirando verticalmente f(x) = x2 + 1 por un factor de escala de 3. ¿Cuál de las siguientes es la expresión correcta para g(x)?
- g(x) = 3×2 + 1
- g(x) = x2 + 3
- g(x) = 3×2 + 3
- g(x) = 3(x + 1)2
- Si g(x) = 4|x|, la función g(x) se estira verticalmente por un factor de escala de ________.
- Si la gráfica de f(x) se estira verticalmente por un factor de 2 para obtener h(x), entonces h(x) = ___ ∙ f(x).
- Si la gráfica de f(x) se estira verticalmente por un factor de 3, la expresión para h(x) es ________.
Solución
Cuando estiramos una función verticalmente, multiplicamos la función base por su factor de escala. Por tanto, tenemos g(x) = 3 – f(x). Asegurémonos de repartir 3 a cada uno de los términos de f(x).
g(x) = 3(x2 + 1)
=3×2 + 3
Esto significa que la expresión correcta para g(x) es 3×2 + 3.
Ejemplo 2
La tabla de valores de f(x) se muestra a continuación. Si g(x) = 4-f(x), construye una tabla de valores para la función g(x).
| x | -6 | -4 | -..2 | 2 | 4 | 6 | f(x) | 9 | 4 | 1 | 1 | 4 | 9 |
Solución
Dado que g(x) = 4-f(x), la función g(x) está estirada verticalmente por un factor de escala de 4. Qué significa esto para su tabla de valores? 9 =
Multiplicamos cada valor de f(x) por 4 para encontrar los valores de salida de g(x). Ten en cuenta que los valores de las coordenadas x seguirán siendo los mismos.
| x | -6 | -4 | -2 | 2 | 4 | 6 |
| g(x) | 36 | 16 | 4 | 4 | 16 | 36 |
Ejemplo 3
Rellena los espacios en blanco para que las siguientes afirmaciones sean verdaderas, dado que f(x) = |x|.
Solución
- Comparando g(x) y f(x), tenemos g(x) = 4 ∙ f(x). Esto significa que la función g(x) se estira verticalmente por un factor de 4.
- Estirar f(x) verticalmente por un factor de 2 dará como resultado que h(x) sea igual a 2 veces f(x).
- Estirar f(x) verticalmente por un factor de 3 dará como resultado que h(x) sea igual a 3 veces f(x). Por tanto, h(x) = 3|x|.
Ejemplo 4
Observa las dos funciones que se muestran a continuación y relaciona h(x) con g(x).
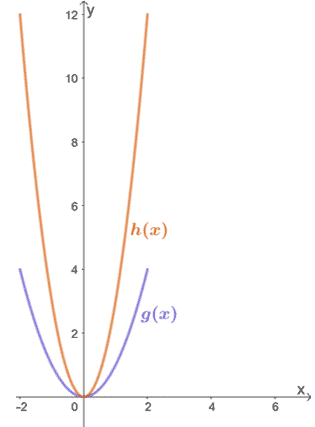
Solución
Sólo por la inspección, podemos ver que h(x) resulta de estirar verticalmente g(x). Para encontrar el factor por el que se estiró h(x), inspeccionemos algunos valores correspondientes para g(x) → h(x).
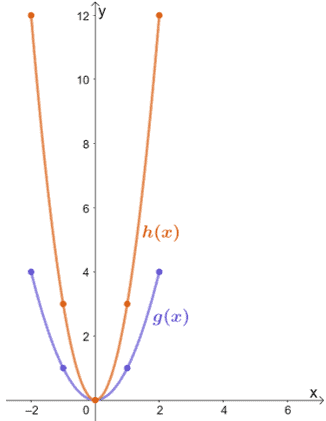
- (0, 0) → (0, 0)
- (1, 1) → (1, 3)
- (2, 4) → (1, 12)
- (-3, 3) → (-3, 9)
- (-1, 1) → (-1, 3)
- (0, 0) → (0, 0)
- (1, 1) → (1, 3)
- (3, 3) → (3, 9)
Podemos ver que la coordenada y de h(x) es tres veces la de g(x) para cada par de puntos. Esto significa que h(x) = 3 ∙ g(x), por lo que h(x) es el resultado de que g(x) se estire verticalmente por un factor de escala de 3.
Ejemplo 5
La función, A(x), modela la distancia (en km) recorrida por el coche A en un periodo de tiempo (en horas).
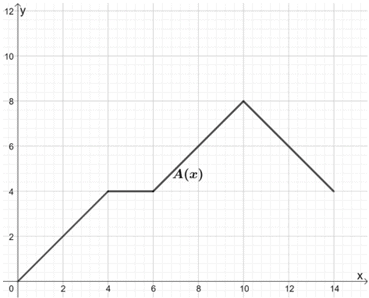
Jack quería comparar este modelo con B(x), cuyo movimiento sigue el mismo patrón, pero el coche que se observa puede cubrir dos veces la distancia de A(x). Utiliza la gráfica de A(x) para dibujar la gráfica de B(x).
Solución
Dado que B(x) = 2 ∙ A(x), estiramos verticalmente la gráfica de A(x) en un factor de escala de 2.
Para ello, podemos tomar nota de algunos puntos de la gráfica y encontrar sus correspondientes valores para B(x). Para encontrar los nuevos pares ordenados, vamos a multiplicar cada coordenada y por 2.
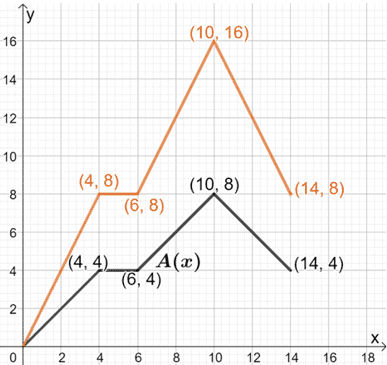
Podemos conectar estos puntos para formar B(x). Ten en cuenta que la forma de A(x) y su base deben seguir siendo las mismas.
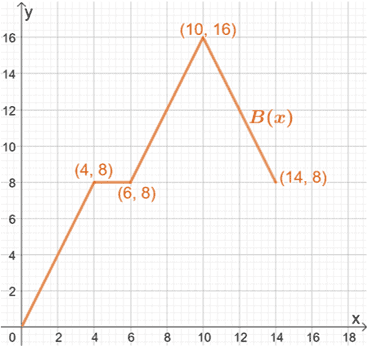
Así, tenemos la gráfica final de B(x), como se muestra arriba.
Ejemplo 6
Observa las dos funciones que se muestran a continuación y relaciona h(x) con g(x). Cuál es la expresión de h(x)?
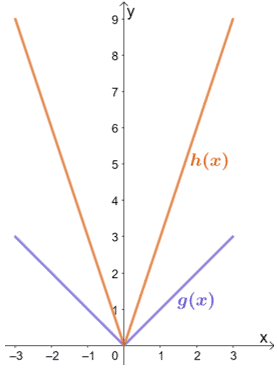
Solución
Podemos ver que h(x) es el resultado de que g(x) se estire verticalmente por un determinado factor de escala. Pasemos a inspeccionar algunos de los puntos correspondientes.
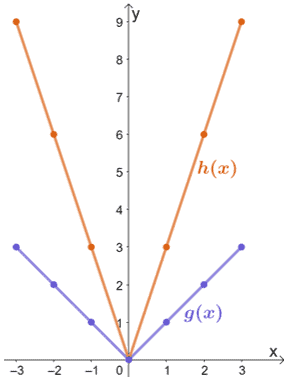
A partir de esto, podemos ver que cuando g(x) se estira verticalmente por un factor de escala de 3, la gráfica resultante será la de h(x). Por tanto, tenemos que h(x) = 3 ∙ g(x).
La función g(x) representa la función madre de todas las funciones de valor absoluto. Esto significa que g(x) = |x|. Para encontrar la expresión de h(x), multiplicamos la expresión de g(x) por 3. Por tanto, tenemos h(x) = 3|x|.
Ejemplo 7
Encuentra las transformaciones realizadas sobre f(x) para obtener h(x).
- f(x) = x2 → h(x) = 3×2 + 24x + 48
- f(x) = √x → h(x) = 2√(x + 2)
- f(x) = ex → h(x) = 5(ex – 2) – 1
.
Solución
- Intentemos primero factorizar la expresión de h(x) para ver si podemos encontrar las transformaciones aplicadas sobre f(x). Comienza factorizando h(x):
- h(x) = 3(x2 + 8x + 16) = 3(x + 4)2 = 3 ∙ f(x + 4)
- A partir de esta forma factorizada, podemos ver que h(x) es el resultado cuando f(x) se traslada 4 unidades a la izquierda y se estira verticalmente en 3.
- Toma nota del factor multiplicado a √x y la unidad restada al valor de entrada.
- Esto da como resultado h(x) = 2 ∙ f(x + 2).
- Por lo tanto, f(x) debe trasladarse 2 unidades a la izquierda y estirarse verticalmente en 2.
- Observemos la diferencia entre ex y h(x).
- h(x) = 5 ∙ ex – 2 -1 , por tanto, tenemos h(x) = 5 ∙ f(x – 2) – 1.
- Esto significa que f(x) se traslada 2 unidades hacia la derecha, se estira verticalmente en 5 y se traslada una unidad hacia abajo.
Ejemplo 8
Solución
Intentemos primero factorizar la expresión de h(x) para ver si podemos encontrar las transformaciones aplicadas sobre f(x).
Comienza por factorizar el factor común que comparten los tres términos.
2×2 – 4x + 2 = 2(x2 – 2x + 1)
Factoriza la expresión usando (a – b)2 = a2 – 2ab + b2.
2(x2 – 2x + 1) = 2(x – 1)2
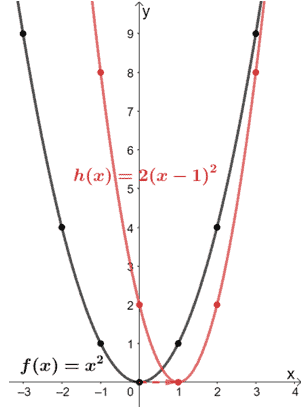
Por tanto, tenemos h(x) = 2(x – 1)2. A partir de esta forma, podemos ver lo siguiente:
- Desde (x – 1)2, podemos ver que f(x) se trasladó una unidad a la derecha.
- La gráfica resultante se estiró entonces verticalmente por un factor de 2.
Usemos estas transformaciones y la gráfica de f(x) para graficar h(x). Así, empezamos trasladando la función padre y = x2 una unidad a la derecha.
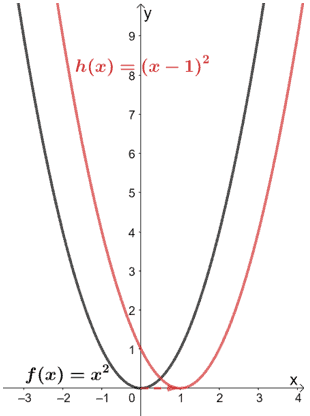
Ahora, vamos a estirar la gráfica verticalmente por un factor de escala de dos.
Quitemos la función de referencia y devolvamos la gráfica final de h(x).
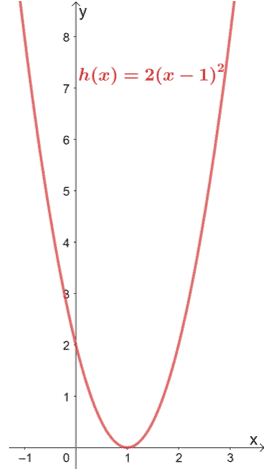
Este ejemplo muestra cómo las transformaciones pueden ahorrar tiempo en la graficación de familias de funciones.
Preguntas de práctica
1. La función, g(x), se obtiene estirando verticalmente f(x) = 3×3 + 2 por un factor de escala de 4. ¿Cuál de las siguientes es la expresión correcta para g(x)?
a. g(x) = 3×3 + 8
b. g(x) = 3×3 + 6
c. g(x) = 12×3 + 2
d. g(x) = 12×3 + 8
2. La tabla de valores de f(x) se muestra a continuación. Si g(x) = 3-f(x), construye una tabla de valores para la función g(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -27 | -8 | -1 | 0 | 1 | 8 | 27 |
3. Completa los espacios en blanco para que las siguientes afirmaciones sean verdaderas, dado que f(x) = √x.
a. Si g(x) = 5√x, la función g(x) está estirada verticalmente por un factor de escala de ________.
b. Si la gráfica de f(x) se estira verticalmente por un factor de 4 para obtener h(x), entonces h(x) = ___ ∙ f(x).
c. Si la gráfica de f(x) se estira verticalmente un factor de 2, la expresión de h(x) es ________.
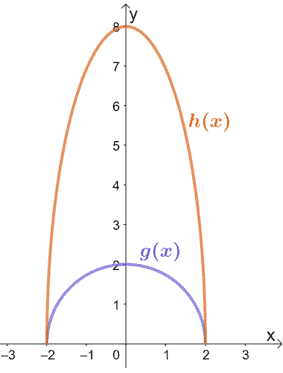
4. Observa las dos funciones que se muestran a continuación y relaciona h(x) con g(x). Si g(x) = √(4 – x2), ¿cuál es la expresión de h(x)?
5. La función, A(x), modela la distancia (en km) recorrida por el coche A a lo largo del tiempo (en horas).
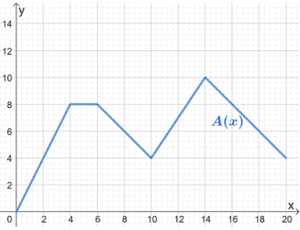
Mary quería comparar este modelo con B(x), cuyo movimiento sigue el mismo patrón, pero el coche que se observa puede recorrer tres veces la distancia de A(x). Utiliza la gráfica de A(x) para dibujar la gráfica de B(x).
6. ¿Qué transformaciones se realizan sobre f(x) para que resulte h(x) = 5x + 6? Utiliza el hecho de que f(x) es la función madre de todas las funciones lineales. Aplica las transformaciones para graficar h(x).
7. Encuentra las transformaciones realizadas para cada par de funciones y grafica h(x) para cada caso.
a. g(x) = x2 → h(x) = 5×2 – 20x + 20
b. g(x) = √x → h(x) = 3√(x – 1)
c. g(x) = 2x → h(x) = 3(2x – 2) + 6
Las imágenes/dibujos matemáticos se crean con GeoGebra.