Introduction aux cercles
L’équation d’un cercle est une extension de la formule de distance.
Objectifs d’apprentissage
Expliquer comment l’équation d’un cercle décrit ses propriétés
Key Takeaways
Key Points
- Un cercle est défini comme l’ensemble des points qui sont à une distance fixe d’un point central.
- La formule de distance peut être étendue directement à la définition d’un cercle en notant que le rayon est la distance entre le centre d’un cercle et le bord.
- L’équation générale d’un cercle, centré sur \left(a,b\right) avec un rayon r, est l’ensemble de tous les points \left(x,y\right) tels que \left(x-a\right)^2+\left(y-b\right)^2=r^2.
- Pi (\pi) est le rapport entre la circonférence d’un cercle et son diamètre.
Termes clés
- diamètre : Deux fois le rayon d’un cercle.
- Aire : La surface intérieure d’un cercle, donnée par A = \pi r^2.
- Cercle : Une figure géométrique à deux dimensions, constituée de l’ensemble de tous les points d’un plan qui sont également distants d’un autre point.
- rayon : Un segment de droite entre tout point de la circonférence d’un cercle et son centre.
La définition d’un cercle est aussi simple que sa forme. Un cercle est l’ensemble de tous les points qui sont à une certaine distance d’un point central. Cette définition est ce qui nous donne le concept du rayon d’un cercle, qui est égal à cette certaine distance.
Puisque nous savons qu’un cercle est l’ensemble des points à une distance fixe d’un point central, regardons comment nous pouvons construire un cercle dans un plan de coordonnées cartésiennes avec les variables x et y. Pour trouver une formule pour cela, supposons que le centre est le point \left(a,b\right). Selon la formule de distance, la distance c du point \left(a,b\right) à tout autre point \left(x,y\right) est:
\displaystyle{c = \sqrt{ \left(x-a\right)^2 + \left(y-b\right)^2}.
Si nous élevons maintenant cette équation au carré des deux côtés, nous avons :
\displaystyle{c^{2} = \left(x-a\right)^{2}+\left(y-b\right)^{2}
Souvenez-vous que la distance entre le centre \left(a,b\right) et tout point \left(x,y\right) sur le cercle est cette distance fixe, qui est appelée le rayon. Changeons donc cette équation pour qu’elle utilise r au lieu de c.
\displaystyle{r^{2} = \left(x-a\right)^{2}+\left(y-b\right)^{2}
C’est la formule générale d’un cercle de centre \left(a,b\right) et de rayon r. Remarquez que tout ce que nous avons fait est de réarranger légèrement l’équation de la formule de distance.

Graphe d’un cercle : Le cercle de centre \left(a,b\right) est graphié dans le plan cartésien.
Parties d’un cercle
Maintenant que nous avons une base algébrique pour le cercle, connectons-la à ce que nous savons déjà sur certaines parties différentes du cercle.
Diamètre
Le diamètre est toute ligne droite qui passe par le centre du cercle. Il est égal à deux fois le rayon, donc :
d = 2r
Circonférence
La circonférence est la longueur du chemin autour du cercle. Algébriquement, elle est donnée par :
c = 2\pi r
ou de manière équivalente par c = \pi d. Le nombre \pi (pi) est défini par cette relation. C’est le rapport entre la circonférence de tout cercle et son propre diamètre.
Aire
L’aire d’un cercle est donnée par :
A = \pi r^2
Notez que le rayon est le seul paramètre définissant la taille de tout cercle particulier, et c’est donc la seule variable dont dépend l’aire.
Introduction aux ellipses
Comprendre l’équation d’une ellipse comme un cercle étiré.
Objectifs d’apprentissage
Connecter l’équation d’une ellipse à l’équation d’un cercle avec des facteurs d’étirement
Principaux points à retenir
Principaux points
- Une ellipse et un cercle sont tous deux des exemples de sections coniques.
- Un cercle est un cas particulier d’ellipse, avec le même rayon pour tous les points.
- En étirant un cercle dans la direction x ou y, on crée une ellipse.
Une ellipse est l’une des formes appelées sections coniques, qui est formée par l’intersection d’un plan avec un cône circulaire droit. L’équation générale d’une ellipse centrée sur \left(h,k\right) est:
{{displaystyle{\frac{\left(x-h\right)^2}{a^2} + \frac{\left(y-k\right)^2}{b^2} = 1}
lorsque le grand axe de l’ellipse est horizontal.

Ellipse : Une ellipse est une section conique, formée par l’intersection d’un plan avec un cône circulaire droit.
Dans la plupart des définitions des sections coniques, le cercle est défini comme un cas particulier de l’ellipse, lorsque le plan est parallèle à la base du cône. Cependant, il est également possible de commencer par la définition d’un cercle et d’utiliser des transformations graphiques pour arriver à la formule générale d’une ellipse.
Rappelons qu’un cercle est défini comme l’ensemble de tous les points équidistants d’un centre commun. Pour simplifier, nous choisirons ce centre comme étant \left(0,0\right), l’origine du plan x-y. Nous pouvons alors écrire l’équation du cercle de cette façon :
x^2 + y^2 = r^2
Dans cette équation, r est le rayon du cercle. Un cercle n’a qu’un seul rayon – la distance entre le centre et tout point est la même. Pour transformer notre cercle en ellipse, nous devrons étirer ou comprimer le cercle afin que les distances ne soient plus les mêmes. Tout d’abord, commençons par un cercle spécifique avec lequel il est facile de travailler, le cercle centré à l’origine et de rayon 1.
x^2 + y^2 = 1
Pour le transformer en ellipse, nous devons déformer la forme circulaire afin qu’elle ne soit plus symétrique entre x et y. Pour ce faire, nous introduisons un facteur d’échelle dans l’une ou les deux coordonnées
x-y. Commençons par diviser toutes les coordonnées x par un facteur a, et donc par mettre à l’échelle les valeurs x. Nous substituons simplement \displaystyle{\frac{x}{a}} dans l’équation à la place de x. Remarque importante : nous supposons que a > 1.
\displaystyle{\left(\frac{x}{a}\right)^2 + y^2 = 1}
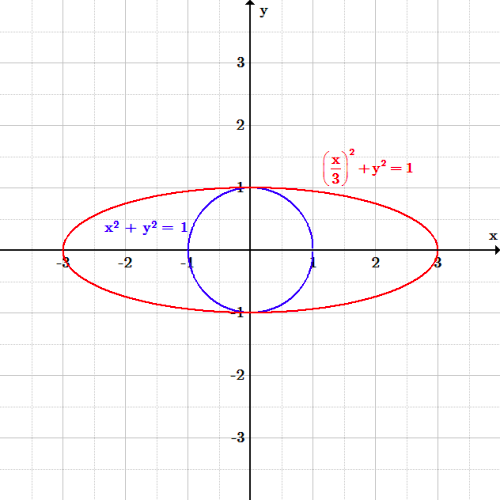
Ellipse selon l’axe des x : L’ellipse \left( \frac{x}{3} \right)^2 +y^2 = 1 a été étirée le long de l’axe des x par un facteur 3 par rapport au cercle x^2 + y^2 = 1.
Chaque valeur de x qui a résolu l’ancienne équation doit maintenant être multipliée par a afin de résoudre la nouvelle équation. Cela a pour effet d’étirer davantage l’ellipse sur l’axe des x, car des valeurs plus grandes de x sont maintenant les solutions.
De même, nous pouvons mettre à l’échelle toutes les valeurs de y par un facteur b (nous supposons également que b > 1).
\displaystyle {x^2 + \left(\frac{y}{b}\right)^2 = 1}
Maintenant toutes les valeurs de y sont étirées verticalement, plus loin de l’origine.
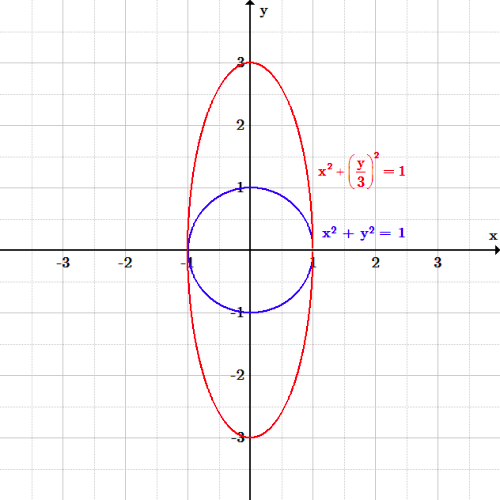
Ellipse selon l’axe des y : L’ellipse x^2 +\left( \frac{y}{3} \right)^2 = 1 a été étirée le long de l’axe des y d’un facteur 3 par rapport au cercle x^2 + y^2 = 1.
Si l’on étire dans les deux directions x et y et que l’on distribue les puissances de deux à travers les parenthèses, on obtient :
\displaystyle{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1}
ce qui est exactement l’équation d’une ellipse horizontale centrée à l’origine.
Si nous avions utilisé des facteurs d’échelle inférieurs à un, cela aurait comprimé la forme au lieu de l’étirer davantage.
Parties d’une ellipse
Les ellipses sont un des types de sections coniques. Les caractéristiques spécifiques d’une ellipse peuvent être déterminées à partir de son équation.
Objectifs d’apprentissage
Discuter comment l’équation d’une ellipse décrit ses propriétés
Principaux points à retenir
Principaux points
- Une ellipse est formée par un plan coupant un cône à un angle par rapport à sa base.
- Toutes les ellipses ont deux points focaux, ou foyers. La somme des distances de chaque point de l’ellipse aux deux foyers est une constante.
- Toutes les ellipses ont un centre et un axe majeur et mineur.
- Toutes les ellipses ont des valeurs d’excentricité supérieures ou égales à zéro, et inférieures à un.
Equation d’une ellipse
Une ellipse est une section conique, formée par l’intersection d’un plan avec un cône circulaire droit. La forme standard de l’équation de l’ellipse est :
\displaystyle{\frac{\left(x-h\right)^2}{a^2} + \frac{\left(y-k\right)^2}{b^2} = 1}
si l’ellipse est orientée horizontalement, et:
{{displaystyle{\frac{\left(y-k\right)^2}{a^2} + \frac{\left(x-h\right)^2}{b^2} = 1}
si l’ellipse est orientée verticalement. Nous allons utiliser le cas horizontal pour montrer comment déterminer les propriétés d’une ellipse à partir de son équation, de sorte que a soit associé aux coordonnées x, et b aux coordonnées y. Pour une ellipse verticale, l’association est inversée.

Diagramme d’une ellipse : Ce diagramme d’une ellipse horizontale montre l’ellipse elle-même en rouge, le centre C à l’origine, les points focaux à \left(+f,0\right) et \left(-f,0\right), les sommets du grand axe à \left(+a,0\right) et \left(-a,0\right), les sommets du petit axe à \left(0,+b\right) et \left(0,-b\right). Il montre également comment la somme des distances de tout point de l’ellipse aux deux foyers est une constante à 2a (la longueur du grand axe), et comment l’excentricité est déterminée par le rapport entre la distance d’un point de l’ellipse à l’un des foyers et la distance perpendiculaire du point à une droite D appelée directrice, extérieure à l’ellipse et perpendiculaire au grand axe.
Parties d’une ellipse
Le centre de l’ellipse a pour coordonnées (h,k).
Axe majeur
Le grand axe de l’ellipse est la plus grande largeur qui la traverse. Pour une ellipse horizontale, cet axe est parallèle à l’axe des x. Le grand axe a une longueur de 2a. Ses points d’extrémité sont les sommets du grand axe, avec les coordonnées (h \pm a, k).
Axe mineur
Le petit axe de l’ellipse est la plus petite largeur à travers elle. Pour une ellipse horizontale, il est parallèle à l’axe des y. Le petit axe a une longueur de 2b. Ses points d’extrémité sont les sommets du petit axe, de coordonnées (h, k \pm b).
Foyers
Les foyers sont deux points à l’intérieur de l’ellipse qui caractérisent sa forme et sa courbure. Pour une ellipse horizontale, les foyers ont pour coordonnées (h \pm c,k), où la distance focale c est donnée par
c^2 = a^2 – b^2
Excentricité
Toutes les sections coniques ont une valeur d’excentricité, notée e. Toutes les ellipses ont des excentricités comprises entre 0 \leq e < 1. Une excentricité de zéro est le cas particulier où l’ellipse devient un cercle. Une excentricité de 1 est une parabole, pas une ellipse.
L’excentricité est définie comme :
\displaystyle{e = \frac{c}{a}}
ou, de manière équivalente :
E &= \frac{\sqrt{a^2 – b^2}}{a}\\\N &= \sqrt{ \frac{a^2 – b^2}{a^2} } \\N &= \sqrt{ 1 – \frac{b^2}{a^2}} \end{align} }
Les orbites des planètes et de leurs lunes sont des ellipses à très faible excentricité, c’est-à-dire qu’elles sont presque circulaires. Les orbites des comètes autour du soleil peuvent être beaucoup plus excentriques. Pour les comètes et les planètes, le soleil est situé à l’un des foyers de leurs orbites elliptiques.
Applications des cercles et des ellipses
Les cercles et les ellipses se rencontrent dans la vie quotidienne, et savoir résoudre leurs équations est utile dans de nombreuses situations.
Objectifs d’apprentissage
Décrire les applications des formules du cercle et de l’ellipse à des problèmes du monde réel
Principaux points à retenir
Principaux points
- La forme standard de l’équation d’un cercle est \left(x-h\right)^2+\left(y-k\right)^2=r^2, où r est le rayon, et \left(h,k\right) est la coordonnée du point central.
- La forme standard de l’équation d’une ellipse est \displaystyle{\frac {\left(x-h\right)^2}{a^2}+\frac {\left(y-k\right)^2}{b^2}= 1}, où \left(h,k\right) est la coordonnée du point central, 2a est la longueur du grand/petit axe, et 2b est la longueur du petit/grand axe.
- Si a>b, le grand axe est parallèle à l’axe x. Si a<b, le grand axe est parallèle à l’axe y (perpendiculaire à l’axe x).
- Pour déterminer les paramètres d’un cercle ou d’une ellipse, il faut d’abord mettre l’équation sous la forme standard.
Termes clés
- Ellipse : Une courbe fermée, le lieu d’un point tel que la somme des distances de ce point à deux autres points fixes (appelés les foyers de l’ellipse) est constante ; de manière équivalente, la section conique qui est l’intersection d’un cône avec un plan qui ne coupe pas la base du cône.
- Cercle : Figure géométrique à deux dimensions, constituée par l’ensemble de tous les points d’un plan qui sont à égale distance d’un autre point.
Les cercles sont partout autour de vous dans la vie quotidienne, des pneus des voitures aux boutons des manteaux, en passant par le dessus des bols, des verres et des bouteilles d’eau. Les ellipses sont moins courantes. Les orbites des planètes en sont un exemple, mais vous devriez être capable de trouver l’aire d’un cercle ou d’une ellipse, ou la circonférence d’un cercle, à partir des informations qui vous sont données dans un problème. Les cercles et les ellipses sont des exemples de sections coniques, qui sont des courbes formées par l’intersection d’un plan avec un cône.
Certains exemples de problèmes sont présentés ci-dessous, avec des solutions travaillées.
Exercice 1
Disons que vous êtes un jardinier, et que vous venez de planter beaucoup de fleurs que vous voulez arroser. Le parterre de fleurs fait 15 pieds de large, et 15 pieds de long. Vous utilisez un système d’arrosage circulaire, et l’eau atteint 6 pieds à partir du centre. L’arroseur est situé, à partir du coin inférieur gauche du parterre, 7 pieds vers le haut, et 6 pieds vers le haut.
- Si le parterre de fleurs était un graphique dont le coin inférieur gauche serait l’origine, quelle serait l’équation du cercle ?
- Quelle est la surface arrosée par l’arroseur ?
- Quel est le pourcentage du jardin qui est arrosé ?
Réponse
Si le coin inférieur gauche est l’origine, il a pour coordonnées \left(0,0\right). À partir de là, l’arroseur se trouve à 6 pieds au-dessus, donc la coordonnée x du centre est 6. L’arroseur est à 7 pieds au-dessus, donc la coordonnée y du centre est 7. Ergo, le centre du cercle est à la coordonnée \left(6,7\right). L’eau atteint 2 mètres de l’arroseur, donc le rayon du cercle est de 2 mètres. Par conséquent, l’équation de ce cercle est :
\displaystyle{\left(x-6\right)^2+\left(y-7\right)^2=36}
La zone qui est arrosée par l’arroseur peut être étiquetée A_{sprinkler}, et est :
\displaystyle{ \begin{align}. A_{sprinkler} &=\pi\cdot r^2\\\ &=\pi\cdot 6^2\\\ &=36\pi \end{align} }
Paradoxalement, on peut dire qu’il s’agit d’un système d’alarme. }
Pour trouver le pourcentage du jardin qui est arrosé, il faut d’abord vérifier qu’aucune eau ne tombe à l’extérieur du jardin. L’arroseur est à la coordonnée \left(6,7\right), et le rayon de l’arroseur est de 6 pieds. Vous pouvez tester que l’eau ne tombe pas en dehors du jardin 15\times 15.
Une fois que nous savons que la zone arrosée est complètement à l’intérieur du jardin, le pourcentage du jardin qui est arrosé peut être trouvé en divisant la zone arrosée par la zone totale du jardin, puis en multipliant par 100\%:
\displaystyle{ \begin{align}. Pourcentage_{arrosé} &=\frac {A_{sprinkler}{A_{flower bed}\cdot 100\%\\\\ &=\frac {36\pi}{15^2}\cdot 100\%\\d &=\frac {113.1}{225}\cdot 100\%\\\\\ &=50.3\% \end{align}
Exercice 2
Maintenant, prenons l’inverse. (x – 4)^2+(y+8)^2=49 est l’équation d’un cercle.
- Quelles sont les coordonnées du centre du cercle ?
- Quel est le rayon ?
- Dessinez le cercle.
- Trouvez deux points sur le cercle et branchez-les dans l’équation pour vous assurer que votre dessin est correct.
Réponse
Le centre du cercle peut être trouvé en comparant l’équation de cet exercice à l’équation d’un cercle :
Gauche(x-h\right)^2+Gauche(y-k\right)^2=r^2
Le centre du cercle est à la coordonnée \left(h,k\right), et donc le centre du cercle dans cet exercice est à \left(4,-8\right).
Le rayon du cercle est r. D’après l’équation d’un cercle, \displaystyle{r^2=49}. Par conséquent :
\displaystyle{ \begin{align} r^2 &= 49 \\ r &= \sqrt{49} \\N &= 7 \end{align} }
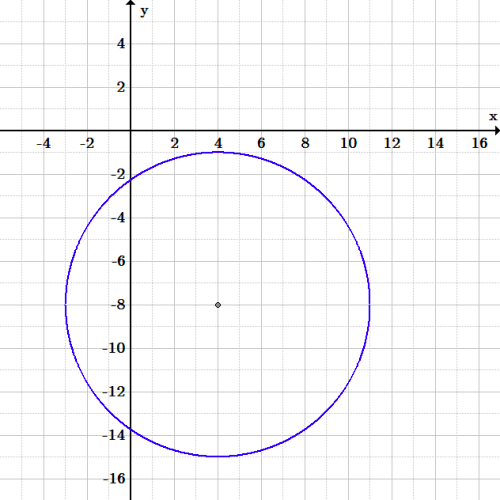
Exercice 2 cercle : Graphique du cercle (x – 4)^2+(y+8)^2=49.
Il y a plusieurs points que vous pourriez choisir. Par exemple, le point \left(4, -1\right) est au sommet du cercle. En le branchant dans l’équation, on obtient :
\displaystyle{ \begin{align} \left(x-h\right)^2+\left(y-k\right)^2 &=r^2 \\\N (4-4)^2+(-1+8)^2 &= 49 \\\\\\N- (0)^2 + (7)^2 &= 49 \N- &= 49 \end{align} }
Le côté gauche est égal au côté droit de l’équation, et c’est donc un point valide sur le cercle.
Le point le plus à gauche du cercle est (-3,-8). En branchant ceci à l’équation :
\displaystyle{ \begin{align} \left(x-h\right)^2+\left(y-k\right)^2 &=r^2 \\left(-3-4\right)^2+\left(-8+8\right)^2 &= 49 \\\\\\N (-7)^2 + (0)^2 &= 49 \N &= 49 \end{align} }
Le côté gauche est égal au côté droit de l’équation, et c’est donc un point valide sur le cercle.
Exercice 3
- Mettez 2x^2+2y^2+8x+24y+60=0 sous la forme standard du cercle : (x-h)^2+(y-k)^2=r^2.
- Quel est le centre et le rayon du cercle ?
- Dessinez le cercle.
- Trouvez deux points sur le cercle et branchez-les dans l’équation pour vous assurer que votre dessin est correct.
Réponse
D’abord, divisez l’équation par le coefficient de x^2 et y^2, qui est 2 :
Style d’affichage{\i} 2x^2+2y^2+8x+24y+60 &=0 \\\frac{2x^2+2y^2+8x+24y+60}{2} &=\frac{0}{2} \\ \frac{2x^2}{2}+\frac{2y^2}{2}+\frac{8x}{2}+\frac{24y}{2}+\frac{60}{2} &=\frac{0}{2} \\N- x^2+y^2+4x+12y+30 &=0 \end{align} }
Puis, rassemblez les termes x et y, et amenez le nombre sur le côté droit de l’équation :
(x^2+4x)+(y^2+12y)=-30
Maintenant, complétez le carré dans les deux parenthèses, en soustrayant ou en ajoutant la constante nécessaire aux deux côtés de l’équation :
\displaystyle{ \begin{align} (x^2+4x+4)+(y^2+12y+36) &=-30+4+36 \N (x^2+4x+4)+(y^2+12y+36) &= 10 \end{align} }
Notez que chaque terme est un carré parfait, ce qui donne :
(x+2)^2+(y+6)^2=10
C’est maintenant sous la forme standard de l’équation d’un cercle.
Le centre du cercle est à la coordonnée \left(h,k\right), et donc le centre du cercle dans cet exercice est à \left(-2,-6\right).
Le rayon du cercle est r. D’après l’équation d’un cercle, \displaystyle{r^2=10}. Par conséquent :
\displaystyle{ \begin{align} r^2 &= 10 \\ r &= \sqrt{10} \end{align} }
Il est bon de laisser la valeur de r sous cette forme.
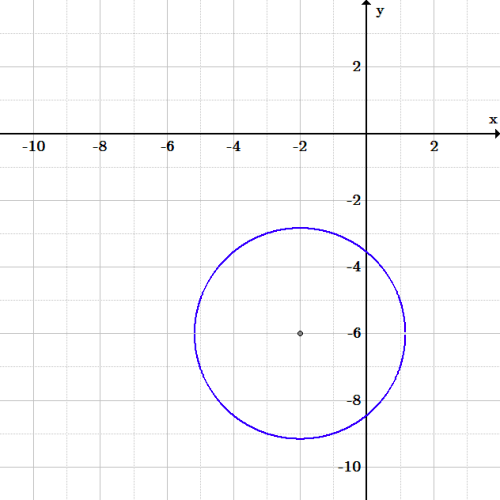
Exercice 3 cercle : Graphique du cercle 2x^2+2y^2+8x+24y+60=0.
Il y a beaucoup de points que vous pourriez choisir. Par exemple, (-5,-5) et (-3, -9) :
\displaystyle{ \begin{align} (-5+2)^2 + (-5 + 6)^2 &&&&= 10 \end{align}
Style d’affichage{\r} \begin{align} (-3+2)^2 + (-9+6)^2 &&= 10 \\N 1 + 9 &= 10 \N 10 &= 10 \end{align}
Les deux sont des points valides sur le cercle.
Exercice 4
- Mettez l’équation \displaystyle{ \frac{4x^2}{9}
- Quel est le centre ?
- Quelle est la longueur du grand axe ?
- Quelle est la longueur du petit axe ?
- Graphiez-la.
Réponse
Cela ressemble presque à une ellipse sous forme standard, n’est-ce pas ? Il y a même un nombre sur le côté droit. Mais ce n’est pas le cas. Il n’y a pas de place dans la forme standard pour les valeurs 4 et 25 dans les numérateurs. Comment s’en débarrasser pour se mettre sous forme standard ?
Réécrire le terme de gauche, \displaystyle{\frac{4x^2}{9}}, en divisant le haut et le bas de la fraction par 4. Laissez le bas comme une fraction ; n’en faites pas un décimal.
Réécrivez le terme de droite, 25y^2, sous la forme \displaystyle{\frac{25y^2}{1}}, en divisant le haut et le bas de la fraction par 25. Laissez le bas comme une fraction ; n’en faites pas un décimal.
L’équation est maintenant :
\displaystyle{ \begin{align} \frac{4x^2}{9} + 25y^2 &= 1 \frac{\frac{\frac{{4x^2}{4}}{\frac{{9}{4}}} + \frac{\frac{25y^2}{25}}{\frac{1}{25}} &= 1 \\frac{x^2}{\frac{9}{\frac{4}} + \frac{y^2}{\frac{1}{25}} &= 1 \end{align} }
D’après l’équation standard, \displaystyle{\frac {\left(x-h\right)^2}{a^2}+\frac {\left(y-k\right)^2}{b^2}= 1}, nous savons que le centre est à \left(h,k\right). Comme ils sont tous deux nuls dans cette équation, le centre est à \left(0,0\right).
Le grand axe dépend de ce qui est le plus long, a ou b. Résolvons les deux, et trouvons lequel est le plus grand par la suite.
\displaystyle{ \begin{align} a^2 &= \frac{9}{4} \\N a &= \frac{3}{2} \\N- 2a &= \frac{6}{2} \\N &= 3 \end{align}
Style d’affichage{\r} b^2 &= \frac{1}{25} \\N- b &= \frac{1}{5} \ 2b &= \frac{2}{5} \end{align} }
Depuis \displaystyle{3>\frac{2}{5}}, 2a>2b, et 2a est le grand axe. La longueur du grand axe est 2a = 3, et la longueur du petit axe est \displaystyle{2b = \frac{2}{5}}.
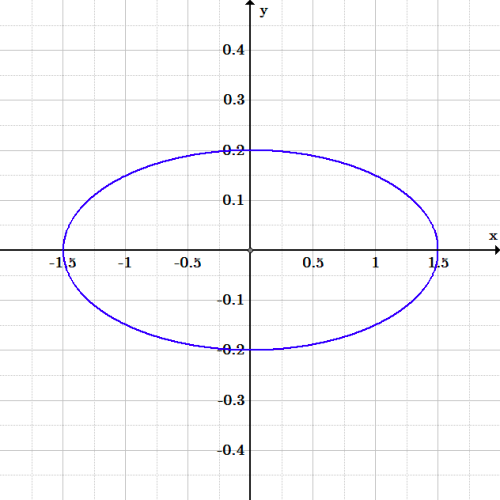
Exercice 4 ellipse : Graphique de l’ellipse \frac{4x^2}{9} + 25y^2 = 1.