L’analyse factorielle est une procédure statistique permettant de décrire les interrelations entre un certain nombre de variables observées. L’analyse factorielle est utilisée pour mesurer des variables qui ne peuvent pas être mesurées directement, pour résumer de grandes quantités de données, et pour développer et tester des théories. Il existe deux grandes catégories d’analyse factorielle : exploratoire et confirmatoire. Les techniques d’analyse factorielle exploratoire ont une histoire beaucoup plus longue que les techniques d’analyse factorielle confirmatoire. Les différences dans les approches conduisent à des utilisations différentes (par exemple, le développement de la théorie par rapport à la confirmation de la théorie).
Purposes
L’analyse factorielle a trois objectifs fondamentaux. Premièrement, elle est utile pour mesurer des constructions qui ne peuvent pas être facilement observées dans la nature. Par exemple, nous ne pouvons pas entendre, voir, sentir, goûter ou toucher l’intelligence, mais elle peut être déduite de l’évaluation de variables observables telles que la performance à des tests d’aptitude spécifiques. L’analyse factorielle est également utile dans le développement d’échelles pour mesurer les attitudes ou d’autres constructions latentes en évaluant les réponses à des questions spécifiques. Deuxièmement, l’analyse factorielle est utile pour résumer un grand nombre d’observations en un plus petit nombre de facteurs. Par exemple, il existe des milliers de descripteurs de la personnalité dans la langue anglaise. Grâce à l’analyse factorielle, les chercheurs ont pu réduire le nombre de facteurs distincts nécessaires pour décrire la structure de la personnalité. Troisièmement, l’analyse factorielle est utile pour fournir des preuves de la validité du construit (par exemple, la validité factorielle, convergente et discriminante). Par exemple, si certaines variables observables sont théoriquement liées les unes aux autres, alors l’analyse factorielle devrait démontrer ces relations théoriques, démontrant simultanément que les mêmes variables sont raisonnablement non corrélées avec les variables d’autres facteurs latents. Ces trois utilisations de l’analyse factorielle peuvent être employées dans le développement et la vérification des théories psychologiques.
Modèle factoriel de base
Le problème de base de l’analyse factorielle prend un certain nombre de variables observables et explique leurs interrelations d’une manière analogue à une équation de régression. Le modèle factoriel commun est une équation de régression dans laquelle les facteurs communs agissent comme des prédicteurs des variables X observées. Le modèle factoriel de base est représenté dans l’équation 1.
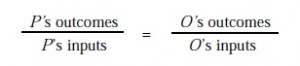
Dans cette équation, X est la matrice des variables observées, L est la matrice des charges factorielles ou des poids de régression, f est la matrice des facteurs communs et u est la matrice des résidus. L’objectif est d’expliquer les interrelations entre les variables X par les facteurs communs, f, et les termes d’erreur résiduels, appelés unicité. La variance de X est divisée en composantes communes et spécifiques. Contrairement à la régression, cependant, les prédicteurs, f, sont inconnus.
Pour fournir un exemple fictif de ce problème, supposons qu’on demande à un certain nombre de superviseurs d’évaluer la pertinence de six caractéristiques de personnalité pour une performance professionnelle efficace des subordonnés. Les caractéristiques évaluées sont organisées, systématiques, négligentes, créatives,
intellectuelles et imaginatives. Le tableau 1 représente la matrice de corrélation hypothétique de ces variables. Le problème de l’analyse factorielle consiste à expliquer les relations entre ces variables avec moins de six facteurs latents sous-jacents. Organisé, systématique et négligent sont tous corrélés les uns avec les autres, mais ils ne sont pas corrélés avec créatif, intellectuel et imaginatif. De même, les variables créative, intellectuelle et imaginative sont toutes corrélées entre elles, mais elles ne sont pas corrélées avec les variables organisée, systématique et négligente. Il existe deux ensembles de corrélations reflétant deux facteurs sous-jacents.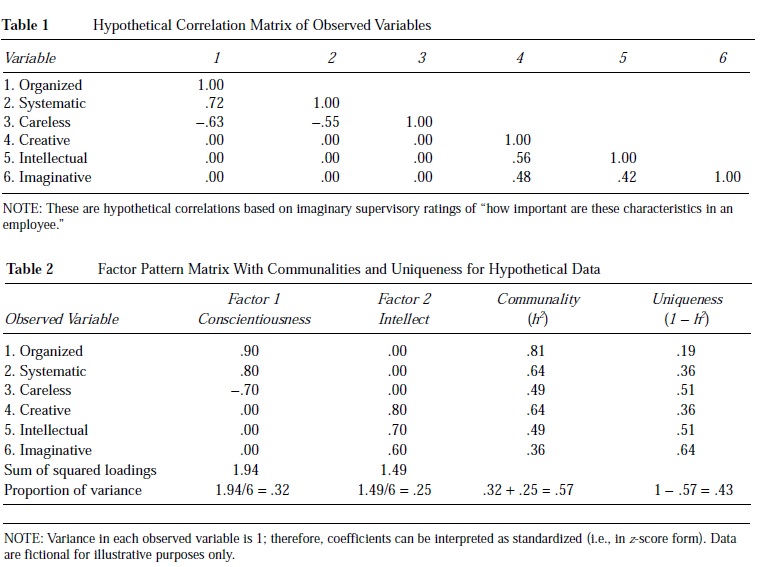
Le tableau 2 représente la matrice des patrons factoriels pour ces variables et les facteurs latents correspondants. Les coefficients de pattern du tableau 2 (colonnes 2 et 3) sont les corrélations des variables observées avec les facteurs. Différentes matrices de motif ou de chargement présenteront différents types de corrélations (par exemple, corrélations de Pearson, corrélations partielles).
La communalité (h2) dans la colonne 4 du tableau 2 représente la variance que la variable a en commun avec les facteurs qu’elle représente. La communalité est analogue à une corrélation multiple au carré dans la régression. L’unicité de la colonne 5 représente la variance spécifique à une variable et non prise en compte par le facteur. L’unicité est analogue à la variance résiduelle de la variable observée après prise en compte des facteurs. Les six variables fictives représentent deux facteurs non observables, chaque facteur expliquant de 36% à 81% de la variance des variables observées.
En plus de la variance associée aux variables observées, la solution de l’analyse factorielle décrit la variance des facteurs eux-mêmes. La somme des charges au carré (SSL) pour un ensemble de variables décrit la variance de chaque facteur. Avant toute transformation des charges factorielles, ces SSL sont appelées valeurs propres. Idéalement, un petit nombre de facteurs rendra compte d’une grande partie de la variance des variables observées. Le tableau 2 montre que les facteurs représentent 32% et 25%, soit un total de 57% de la variance des variables observées. Les 43% restants de la variance des variables observées ne sont pas communs aux facteurs.
Analyse factorielle exploratoire
Typiquement, le but de l’analyse factorielle exploratoire (AFE) est de laisser les données déterminer les interrelations entre un ensemble de variables. Bien qu’un chercheur utilisant l’AFE puisse avoir une théorie reliant les variables les unes aux autres, il y a relativement peu de restrictions sur le modèle factoriel de base dans une AFE. Ce type d’analyse a été utile dans le développement de la théorie et le débat depuis plus d’un siècle.
L’analyse factorielle exploratoire est particulièrement appropriée dans les premiers stades du développement de la théorie et dans les premiers stades du développement de l’échelle ou du test. Tout d’abord, l’AFE est utile dans la réduction des données lorsque les interrelations entre les variables ne sont pas spécifiées au préalable. Un chercheur utilisant l’AFE fait appel au raisonnement inductif en prenant un certain nombre d’observations et en développant une théorie à partir de ces observations. Dans l’exemple des caractéristiques des employés très performants, six variables de personnalité ont finalement été réduites à deux facteurs. Pour les analyses ultérieures, il n’est donc nécessaire d’examiner que deux variables plutôt que les six variables initiales. La réduction des données est particulièrement utile pour atténuer les problèmes de multi-collinéarité (corrélations trop élevées) entre un ensemble de prédicteurs. Un deuxième avantage de l’AFE est la possibilité de détecter un facteur général. Lorsque plusieurs tests d’aptitudes cognitives spécifiques font l’objet d’une analyse factorielle, un facteur général tend à émerger, ainsi que plusieurs facteurs spécifiques. Dans l’évaluation de l’intelligence, par exemple, tous les tests d’aptitude sont corrélés dans une certaine mesure avec le facteur général de l’intelligence, ou g.
Enfin, l’AFE est particulièrement utile dans le développement d’échelles ou de tests, car elle permet au chercheur de déterminer la dimensionnalité du test et de détecter les charges croisées (corrélations des variables avec plus d’un facteur). Les charges croisées ne sont généralement pas souhaitables. Dans le développement d’une échelle, il est avantageux d’avoir des items qui se rapportent à un seul facteur. Pour l’exemple précédent, les trois variables représentant la conscience ne se chargent pas de manière croisée sur l’intellect et vice versa.
Analyse factorielle confirmatoire
Le but de l’analyse factorielle confirmatoire (AFC) est de tester des hypothèses dérivées théoriquement étant donné un ensemble de données. Le modèle factoriel de base de l’équation 1 est toujours pertinent, mais certaines restrictions sont imposées étant donné le modèle théorique particulier testé. Par exemple, dans l’exemple précédent, on pourrait utiliser l’AFC pour imposer des restrictions sur le modèle factoriel afin d’interdire les charges croisées. Développée au cours des années 1960, l’AFC est un développement statistique plus récent que l’AFE (développée en 1904).
L’analyse factorielle confirmatoire est particulièrement utile dans un processus de raisonnement déductif. La vérification d’hypothèses spécifiques est possible lorsqu’on utilise l’AFC. Par exemple, un chercheur peut se pencher sur la signification statistique des charges factorielles individuelles. Dans l’exemple précédent, étant donné la corrélation relativement faible, on pourrait déterminer avec une certitude statistique le degré de corrélation de la variable observée, l’imagination, avec le facteur latent, l’intellect.
Avec l’AFC, il est possible de tester l’hypothèse selon laquelle deux facteurs par rapport à un seul facteur (ou toute autre combinaison numérique) sous-tendent un ensemble de données. Dans l’AFE, les chercheurs s’appuient sur des règles empiriques et l’intuition, ce qui peut égarer le chercheur, mais dans l’AFC, les modèles peuvent être explicitement comparés grâce à des tests statistiques d’hypothèses nulles. Une autre utilisation de l’AFC consiste à évaluer l’équivalence des parties du modèle factoriel de base dans un ensemble de données donné. Par exemple, on peut supposer que toutes les variables observées pour l’intellect sont également liées à l’intellect. Avec l’AFC, l’équivalence de ces relations peut être testée en imposant des contraintes sur les chargements dans le modèle factoriel de base (c’est-à-dire L dans l’équation 1).
Il est également important de déterminer si les résultats d’une analyse factorielle sont similaires entre les groupes démographiques. L’analyse factorielle confirmatoire permet de tester l’invariance – c’est-à-dire l’équivalence de la structure factorielle, des chargements, de l’unicité – entre différents groupes (par exemple, ethniques, de sexe, culturels) d’individus. Un chercheur pourrait vouloir savoir si la même structure factorielle hypothétique émergerait si l’on comparait les réponses des superviseurs de travailleurs de la fabrication à celles des superviseurs de travailleurs des services. Il se peut que les variables observées ne soient pas liées aux facteurs latents de la même manière pour les deux groupes. Par exemple, l’indicateur systématique observé peut être moins lié au facteur consciencieux pour les travailleurs des services que pour les travailleurs de la fabrication. Dans une AFC qui teste l’équivalence des charges factorielles, un chercheur peut tester l’hypothèse selon laquelle les corrélations des deux groupes sont identiques ou différentes.
L’analyse factorielle confirmatoire présente une plus grande souplesse de contrôle que l’AFE. Avec l’AFC, certains facteurs peuvent être spécifiés comme obliques (corrélés les uns aux autres), tandis que d’autres sont spécifiés comme orthogonaux (non corrélés les uns aux autres). Dans un seul AFC, les facteurs sont interprétés comme étant soit obliques, soit orthogonaux, mais pas une combinaison des deux. En outre, l’AFC permet au chercheur d’imposer avec souplesse des contraintes supplémentaires sous réserve de la théorie (par exemple, autoriser l’unicité de la corrélation). Cependant, un avantage de l’AFE est qu’aucune contrainte ou spécification théorique de ce type n’est nécessaire. Par conséquent, si aucune n’existe, l’AFE peut être un meilleur choix.
- Gorsuch, R. L. (2003). Factor analysis. Dans J. A. Schinka & W. F. Velicer (Eds.), Handbook of psychology : Research methods in psychology (Vol. 2, pp. 143-164). Hoboken, NJ : Wiley.
- Hurley, A. E., Scandura, T. A., Schriesheim, C. A., Brannick, M. T., Seers, A., Vandenberg, R. J., & Williams, L. J. (1997). Analyse factorielle exploratoire et confirmatoire : Guidelines, issues, and alternatives. Journal of Organizational Behavior, 18, 667-683.
- Lance, C. E., & Vandenberg, R. J. (2002). Analyse factorielle confirmatoire. Dans F. Drasgow & N. Schmitt (Eds.), Measuring and analyzing behavior in organizations : Advances in measurement and data analysis (pp. 221254). San Francisco : Jossey-Bass.
- Preacher, K. J., & MacCallum, R. C. (2003). Réparer la machine électrique d’analyse factorielle de Tom Swift. Understanding Statistics, 2, 13-43.
- Thompson, B. (2004). Analyse factorielle exploratoire et confirmatoire : Comprendre les concepts et les applications. Washington, DC : American Psychological Association.
- Vandenberg, R. J., & Lance, C. E. (2000). Un examen et une synthèse de la littérature sur l’invariance des mesures : Suggestions, pratiques et recommandations pour la recherche organisationnelle. Organizational Research Methods, 3, 4-69.
.