L’empilement des tolérances, également appelé empilement des tolérances, fait référence à la combinaison de diverses tolérances sur les dimensions de la pièce. Après avoir identifié une tolérance sur la dimension d’une pièce, il est important de tester si cette tolérance fonctionnerait avec les tolérances de l’outil : soit l’extrémité supérieure, soit l’extrémité inférieure. Une pièce ou un assemblage peut être sujet à des imprécisions lorsque ses tolérances sont empilées de manière incorrecte.
L’importance des tolérances
Les tolérances influencent directement le coût et les performances d’un produit. Des tolérances plus serrées rendent une pièce usinée plus difficile à fabriquer et donc souvent plus chère. Dans cette optique, il est important de trouver un équilibre entre la fabricabilité de la pièce, sa fonctionnalité et son coût.
Conseils pour un empilement de tolérances réussi
Éviter d’utiliser des tolérances inutilement petites
Comme indiqué ci-dessus, des tolérances plus serrées entraînent un coût de fabrication plus élevé, car la pièce est plus difficile à fabriquer. Ce coût plus élevé est souvent dû à l’augmentation de la quantité de pièces mises au rebut qui peut survenir lorsque des dimensions se révèlent hors tolérance. Le coût des porte-outils de haute qualité et de l’outillage avec des tolérances plus serrées peut également être une dépense supplémentaire.
En outre, des tolérances inutilement faibles entraîneront des temps de fabrication plus longs, car il y a plus de travail pour s’assurer que la pièce répond à des critères stricts pendant l’usinage, et après l’usinage dans le processus d’inspection.
Faites attention à ne pas surdimensionner une pièce
Lorsqu’une tolérance supérieure et inférieure est étiquetée sur chaque caractéristique d’une pièce, le surdimensionnement peut devenir un problème. Par exemple, une fraise à rayon d’angle avec des rayons d’angle droit et gauche pourrait avoir une tolérance de +/- 0,001″, et le plat entre eux a une tolérance de 0,002″. Dans ce cas, la fenêtre de tolérance pour le diamètre de la fraise serait de +/- 0,004″, mais elle est souvent mal calculée lors du dimensionnement de la pièce. De plus, placer une tolérance sur cette callout la ferait surdimensionner, et donc la cote de référence « REF » doit être laissée pour prendre la place de la tolérance.
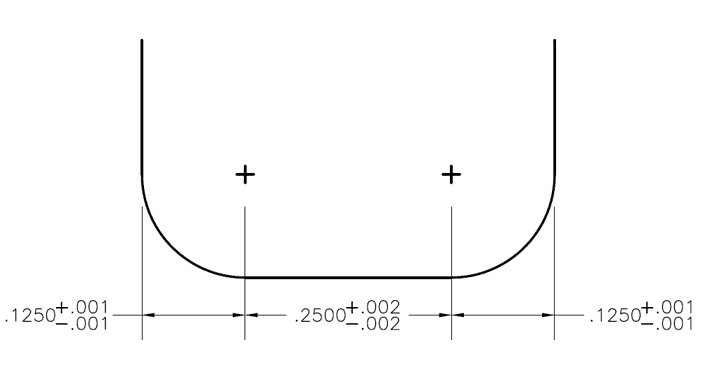
Figure 1 : Forme de la fente créée par une fraise à rayon d’angle
Utiliser l’analyse statistique des tolérances :
L’analyse statistique examine la probabilité que les trois tolérances soient inférieures ou supérieures à la largeur de la fente dimensionnée, en fonction d’un écart type. Cette probabilité est représentée par une fonction de densité de probabilité normale, que l’on peut voir sur la figure 2 ci-dessous. En combinant toutes les probabilités des différentes pièces et dimensions d’une conception, nous pouvons déterminer la probabilité qu’une pièce présente un problème, ou échoue complètement, en fonction des dimensions et de la tolérance des pièces. Généralement, cette méthode d’analyse n’est utilisée que pour les assemblages comportant quatre tolérances ou plus.
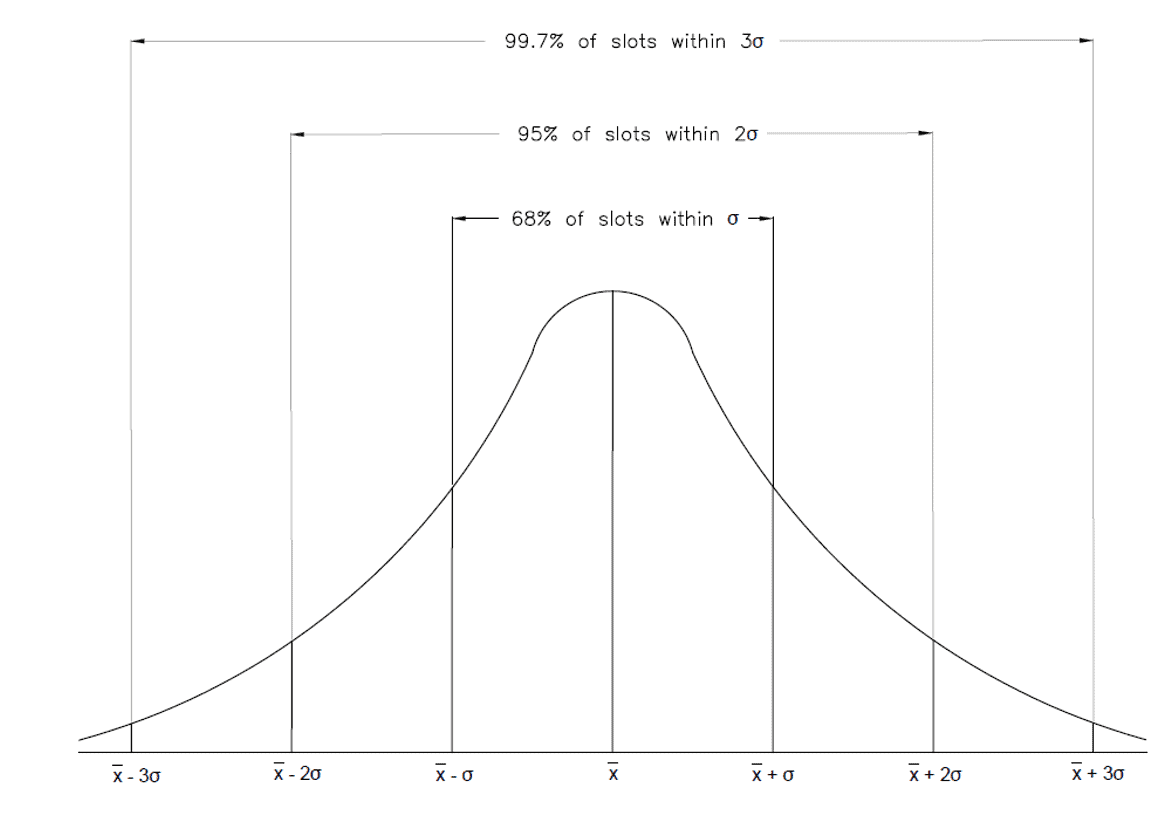
Figure 2 : empilement des tolérances : Distribution normale
Avant de commencer une analyse statistique des tolérances, vous devez calculer ou choisir un facteur de distribution des tolérances. La distribution normale est de 3 . Cela signifie que la plupart des données (ou, dans ce cas, des tolérances) se situeront à moins de 3 écarts types de la moyenne. Les écarts types de toutes les tolérances doivent être divisés par ce facteur de distribution de tolérance pour les normaliser d’une distribution de 3 à une distribution de 1 . Une fois cela fait, on peut prendre la somme des racines au carré pour trouver l’écart type de l’ensemble.
Pensez-y comme à une tasse de café préparée avec 3 grains de taille différente. Afin de préparer une délicieuse tasse de café, vous devez d’abord moudre tous les grains à la même taille afin de pouvoir les ajouter au filtre à café. Dans ce cas, les grains sont les écarts types, le moulin est le facteur de distribution des tolérances et le filtre à café est l’équation de la somme des carrés. Cela est nécessaire car certaines tolérances peuvent avoir des facteurs de distribution différents en fonction de l’étroitesse de la plage de tolérance.
La méthode d’analyse statistique est utilisée s’il y a une exigence selon laquelle la fente doit avoir une largeur de 0,500″ avec une tolérance de +/- 0,003″, mais il n’est pas nécessaire que les rayons (,125″) et le plat (,250″) soient exacts tant qu’ils s’insèrent dans la fente. Dans cet exemple, nous avons 3 tolérances bilatérales avec leurs écarts types déjà disponibles. Puisqu’il s’agit de tolérances bilatérales, l’écart type par rapport à la moyenne sera simplement égal à la valeur de la tolérance + ou -. Pour les rayons extérieurs, ce serait 0,001″ et pour la région plate centrale, ce serait 0,002″.
Pour cet exemple, trouvons l’écart type (σ) de chaque section en utilisant l’équation 1. Dans cette équation représente l’écart type.
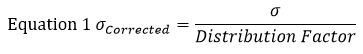
L’hypothèse standard est qu’une tolérance de pièce représente une distribution normale de +/- 3. Par conséquent, le facteur de distribution sera de 3. En utilisant l’équation 1 sur la section gauche de la figure 1, nous trouvons que son écart-type corrigé équivaut à :
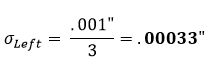
Ce procédé est ensuite répété pour les sections du milieu et de droite :
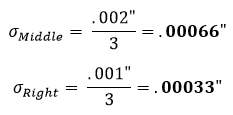
Après être arrivé à ces écarts types, on introduit les résultats dans l’équation 2 pour trouver l’écart type de la zone de tolérance. L’équation 2 est connue comme l’équation de la somme des racines au carré.
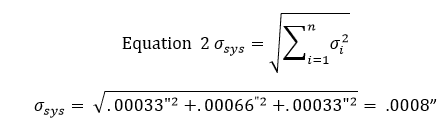
À ce stade, cela signifie que 68 % des fentes seront dans une tolérance de +/- 0,0008″. En multipliant cette tolérance par 2, on obtient une fenêtre de confiance de 95%, où en la multipliant par 3, on obtient une fenêtre de confiance de 99%.
68% des créneaux seront dans une fourchette de +/- .0008″
95% des créneaux seront à +/- 0,0016″
99% des créneaux seront à +/- 0,0024″
Ces fenêtres de confiance sont standard pour un ensemble de points de données distribué normalement. Une distribution normale standard peut être vue dans la figure 2 ci-dessus.
L’analyse statistique des tolérances ne doit être utilisée que pour les assemblages comportant plus de 4 pièces tolérées. Beaucoup de facteurs n’ont pas été pris en compte dans cette analyse simple. Cet exemple concernait 3 dimensions bilatérales dont les tolérances étaient représentatives de leurs écarts types par rapport à leurs moyennes. Dans l’analyse statistique standard des tolérances, d’autres variables entrent en jeu, comme les angles, le faux-rond et le parallélisme, qui nécessitent des facteurs de correction.
Utiliser l’analyse du pire cas :
L’analyse du pire cas consiste à additionner toutes les tolérances d’une pièce pour trouver la tolérance totale de la pièce. Lors de l’exécution de ce type d’analyse, chaque tolérance est fixée à sa limite la plus grande ou la plus petite dans sa plage respective. Cette tolérance totale peut ensuite être comparée aux limites de performance de la pièce pour s’assurer que l’assemblage est conçu correctement. Cette méthode est généralement utilisée pour une seule dimension (Un seul plan, donc pas d’angles impliqués) et pour les assemblages avec un petit nombre de pièces.
L’analyse du pire cas peut également être utilisée lors du choix de l’outil de coupe approprié pour votre travail, car la tolérance de l’outil peut être ajoutée à la tolérance des pièces pour un scénario du pire cas. Une fois ce scénario identifié, le machiniste ou l’ingénieur peut effectuer les ajustements appropriés pour maintenir la pièce dans les dimensions spécifiées sur l’impression. Il convient de noter que le scénario le plus défavorable se produit rarement dans la production réelle. Bien que ces analyses puissent être coûteuses pour la fabrication, elles offrent une certaine tranquillité d’esprit aux machinistes en garantissant que tous les assemblages fonctionneront correctement. Cette méthode exige souvent des tolérances serrées car l’empilement total dans des conditions maximales est la principale caractéristique utilisée dans la conception. Les tolérances plus serrées intensifient les coûts de fabrication en raison de l’augmentation de la quantité de raclage, du temps de production pour l’inspection et du coût de l’outillage utilisé sur ces pièces.
Exemple du pire scénario dans le contexte de la figure 1:
Trouver la limite inférieure des spécifications.
Pour le rayon du coin gauche
.125″ – .001″ = .124″
Pour la section plate
.250″ – .002″ = .248″
Pour le rayon du coin droit
.125″ – .001″ = .124″
Ajoutez tout cela à la limite inférieure des spécifications :
.124″ + .248″ + .124″ = .496″
Trouver la limite supérieure des spécifications:
Pour le rayon du coin gauche