La quatrième dimension est un endroit où l’on peut voyager en allant dans une direction perpendiculaire à la troisième dimension. Pour l’œil non averti, cette affirmation n’a absolument aucun sens. Comment pourrait-il y avoir une direction perpendiculaire à un espace tridimensionnel ? Pour mieux comprendre ce concept, nous devons parcourir lentement toutes les dimensions et analyser les changements qui s’opèrent entre chacune d’elles.

Dimension zéro
La dimension zéro est une dimension à laquelle on ne pense pas souvent. Les points sont les seuls êtres dimensionnels qui peuvent être correctement appréhendés dans la dimension zeroth. Ils n’ont absolument aucune dimension, aucune largeur, aucune longueur, aucune hauteur. Ils sont les plus petits qu’ils puissent jamais être, mais aussi les plus grands qu’ils puissent jamais être en même temps.
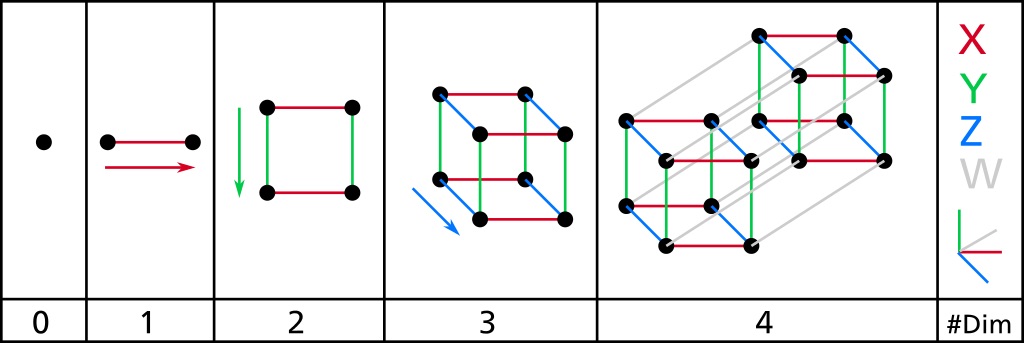
Alors que nous cherchons à approfondir notre compréhension de la quatrième dimension. Nous pouvons examiner un cube dans chaque dimension au fur et à mesure de notre progression. Un cube dans la dimension zéro serait simplement un point. Toutes ses dimensions sont les mêmes dans toutes les directions car il n’y en a pas. Le cube représente toujours un point dans l’espace, mais c’est là toute l’étendue de son pouvoir dans la dimension zéro. Maintenant, passons à la 1-D.
Première dimension
La transition entre la dimension zéro et la première dimension implique une extrusion dans toutes les directions. Dans la première dimension, tout existe sous forme de ligne. La seule chose qui diffère entre les objets dans la première dimension est leur longueur. Les lignes ont toutes la même largeur et la même hauteur, mais leur longueur peut varier.
Si vous voulez faire varier l’épaisseur des lignes, alors vous devez passer aux lignes bidimensionnelles. Un cube dans la première dimension ressemblerait à une ligne ayant la même longueur que ledit cube, mais aucune valeur de largeur ou de hauteur.
Deuxième dimension
Transformer un segment de ligne dans une direction perpendiculaire à la direction à 1 dimension vous fait entrer dans la deuxième dimension. Gardez cette idée à l’esprit à mesure que nous élargissons nos connaissances dimensionnelles et remarquez cette action perpendiculaire répétée à mesure que nous nous déplaçons à travers les dimensions.
Dans la deuxième dimension, notre cube peut commencer à ressembler à un cube, mais à peine. Un cube existerait comme un carré dans la deuxième dimension. Vous pouvez, bien sûr, dessiner une représentation d’un cube 3D en 2 dimensions, mais ce n’est pas ce à quoi ressemblerait un cube en 2 dimensions. Il s’agirait plutôt simplement d’une représentation de la troisième dimension superposée à la deuxième.
La longueur et la largeur peuvent varier dans la deuxième dimension, ce qui permet de créer des formes et une géométrie de base. Lorsque nous passons à la troisième dimension, les mathématiques commencent à devenir plus complexes.
Troisième dimension
Le cube de la deuxième dimension est maintenant extrudé dans une troisième direction perpendiculaire aux deux côtés du carré 2D. Pour mettre cela en termes cartésiens, le carré 2D existait dans les directions X et Y. Le déplacement dans la troisième dimension extrude ce carré dans la direction Z. C’est dans la troisième dimension que notre cube devient réellement un cube au sens traditionnel du terme. L’objet a des dimensions de largeur, de longueur et de hauteur.
Pendant toutes les dimensions, il est important de noter qu’un cube conservera toutes ses propriétés de base en théorie. Tous les angles seront droits et tous les côtés seront identiques. En introduisant un autre principe de dimensions, nous pouvons examiner ce qui se passerait si le cube était agrandi indéfiniment. Lorsqu’un cube dans la troisième dimension est étendu à l’infini, il englobe la totalité de l’espace à 3 dimensions.
Jusqu’ici, vous devriez probablement saisir ces 3 dimensions, après tout, ce sont les dimensions auxquelles nous nous associons le plus communément.
Quatrième dimension
Lorsque nous amenons le cube dans la quatrième dimension, nous commençons à faire l’expérience de mathématiques contre-intuitives. Nous extrudons le cube dans une direction perpendiculaire à toutes les trois premières. Cela est impossible dans la troisième dimension, car il n’y a que trois dimensions dans lesquelles le cube est déjà dilaté. Lorsque nous ajoutons la quatrième dimension, afin de maintenir les propriétés du cube, à savoir que tous les angles sont à 90 degrés et que tous les côtés sont identiques, nous devons extruder dans cette nouvelle dimension.
Les cubes dans les quatrièmes dimensions sont techniquement appelés tesseracts. Les objets en 4D diffèrent en longueur, largeur, hauteur et trength. La superposition de trength sur l’une des dimensions précédentes donne à un objet dans les dimensions suivantes un trength de 0, ou une valeur infiniment petite.
Tous les bords d’un tesseract sont identiques, et tous les angles sont droits. Cela a du sens en théorie, mais lorsque nous commençons à imaginer ce à quoi ressemblerait un tesseract, nous sommes liés par nos esprits tridimensionnels. Pour visualiser un tesseract, nous devons superposer cet objet de quatrième dimension dans la troisième dimension.
La principale façon dont nous représentons un tesseract, ou cube de quatrième dimension, est de le projeter dans la troisième dimension avec la perspective. Cette représentation peut être vue ci-dessous.
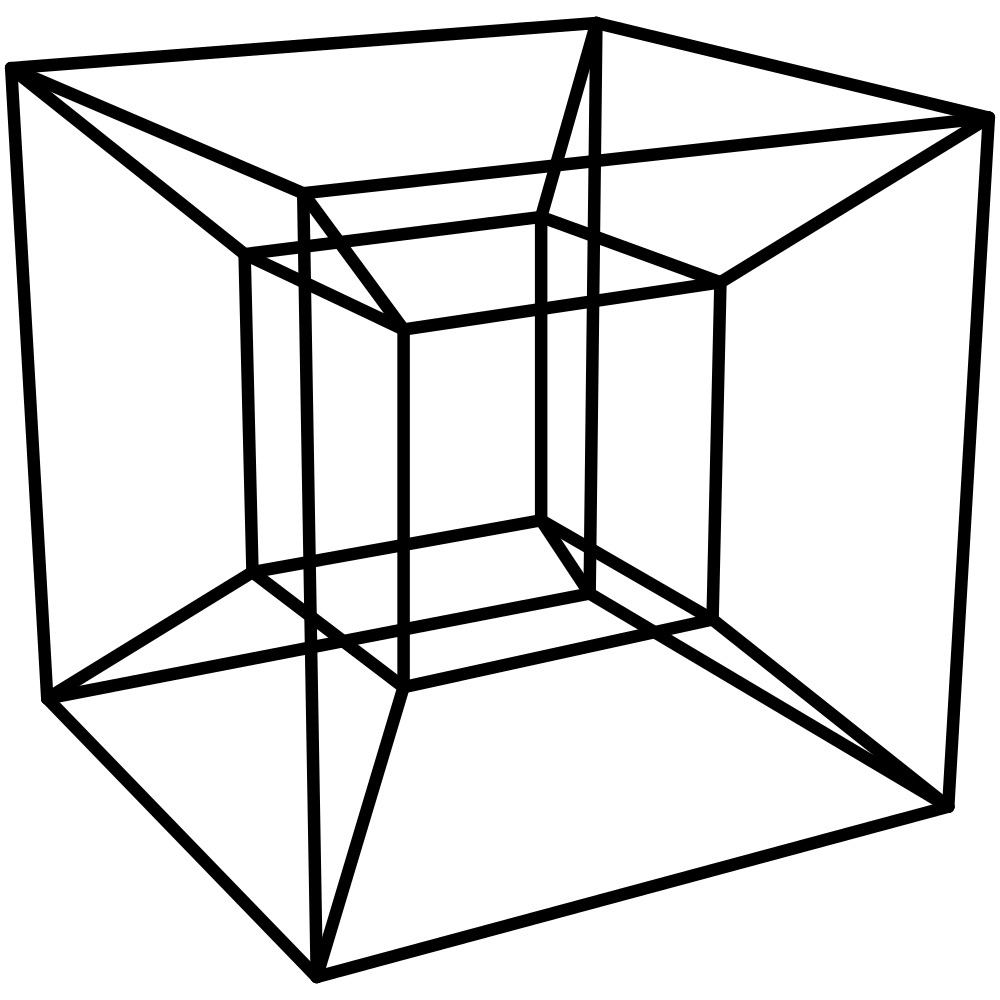
C’est également une représentation en perspective d’un tesseract sous forme de gif.

Cette représentation n’est pas ce à quoi ressemble un cube 4D, c’est simplement ce à quoi il ressemble en perspective vu de la troisième dimension. Pour résumer notre compréhension de la quatrième dimension, les objets en 4D varient en valeur par la longueur, la largeur, la hauteur et la longueur. Toutes ces mesures dimensionnelles s’étendent dans une direction perpendiculaire aux trois précédentes. La largeur est perpendiculaire à la longueur, la hauteur est perpendiculaire à la largeur et à la longueur, et enfin, la trensité est perpendiculaire à la hauteur, à la longueur et à la largeur.
Ces concepts sont difficiles à saisir mais j’espère que cela vous donne une bonne compréhension générale du fonctionnement de la quatrième dimension et de la façon dont nous l’interprétons à partir de nos yeux tridimensionnels.
Cela n’a toujours aucun sens ? Laissez Carl Sagan vous l’expliquer.
La quatrième dimension.