L’équation de Schrödinger, parfois appelée équation d’onde de Schrödinger, est une équation aux dérivées partielles.Elle utilise le concept de conservation de l’énergie (énergie cinétique + énergie potentielle = énergie totale) pour obtenir des informations sur le comportement d’un électron lié à un noyau.Elle le fait en permettant de calculer la fonction d’onde d’un électron, Ψ.

La résolution de l’équation de Schrödinger nous donne Ψ et Ψ2.Avec ceux-ci, nous obtenons les nombres quantiques et les formes et orientations des orbitales qui caractérisent les électrons dans un atome ou une molécule.
L’équation de Schrödinger ne donne des solutions exactes que pour les noyaux à un électron : H, He+, Li2+, Be3+, B4+, C5+, etc.En langage mathématique, on dit que les solutions analytiques de Ψ ne sont possibles que pour les systèmes à un électron.Les systèmes à un électron sont souvent décrits comme hydrogéniques – ce qui signifie » comme l’hydrogène « .
Pour tous les autres atomes, ions et molécules, aucune solution analytique pour Ψ n’est possible ; on utilise alors des méthodes de calcul par approximation, comme l’approximation orbitale et le théorème de variation.
Il existe une équation de Schrödinger dépendante du temps et une équation de Schrödinger indépendante du temps.
L’équation indépendante du temps considère que l’état quantique de l’électron est immuable, elle considère donc l’électron comme une onde stationnaire.L’équation indépendante du temps permet de trouver les densités électroniques (c’est-à-dire les tailles et les formes des orbitales atomiques et moléculaires) en utilisant Ψ2, le carré de la fonction d’onde.
Les orbitales p ci-dessous sont des exemples de Ψ2 :



L’Équation de Schrödinger indépendante du tempsIndépendante du temps
L’équation de Schrödinger indépendante du temps peut être exprimée en sténographie mathématique hautement compressée comme suit :
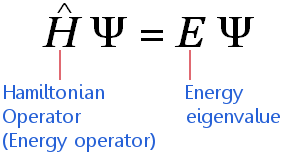
L’équation s’applique aux électrons voyageant à des vitesses non relativistes. (Cela signifie qu’elle nécessite des ajustements avant de pouvoir être appliquée à des éléments de masse élevée.)L’équation dit:
L’équation indépendante du temps peut être écrite dans tout système de coordonnées approprié, comme les coordonnées cartésiennes (x,y,z).Pour les atomes d’hydrogène, les coordonnées polaires sphériques sont plus appropriées, donc :
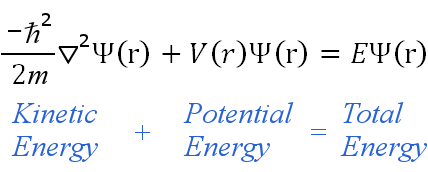
Les contraintes aboutissent à la quantification
On résout l’équation pour trouver Ψ.Les contraintes placées sur la résolution de l’équation produisent une quantification – c’est-à-dire que les solutions trouvées pour Ψ sont limitées à certaines valeurs et que toutes les autres valeurs sont interdites.
Ces contraintes sont :
– Ψ et sa dérivée partielle première doivent être continues.
– Ψ doit être normalisable : cela signifie qu’il existe une probabilité de 100 % que l’électron se trouve quelque part dans l’univers.Pour un Ψ à valeur réelle, la normalisation exige que :
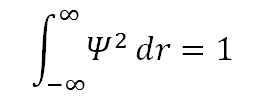
– Lorsque la distance au noyau augmente, l’électron se détache et n’est plus lié.Autrement dit, comme r → ∞, H → H+ + e-.
La fonction d’onde produit des nombres quantiques
La fonction d’onde de l’électron existe en trois dimensions, donc les solutions de l’équation de Schrödinger ont trois parties.Celles-ci sont obtenues explicitement par une méthode de résolution des équations aux dérivées partielles appelée séparation des variables. En faisant cela, on obtient :
Il s’avère que les solutions de Ψ ne sont possibles que lorsque :
– Dans R(r), une constante, appelée n, a pour valeurs 1, 2, 3, 4,…….
– Dans P(θ), une constante, appelée l, a pour valeurs 0, 1, 2, 3,…(n-1)
– Dans F(φ), une constante, appelée ml, a pour valeurs -l, (l+1),…0…., (l+1), l
Et ainsi, à partir de la fonction d’onde Ψ, l’équation de Schrödinger a livré les trois nombres quantiques qui caractérisent le comportement de l’électron dans un atome.
– n : le nombre quantique principal
– l : le nombre quantique de moment angulaire orbital
– ml : le nombre quantique magnétique
La fonction d’onde produit les formes et les tailles des orbitales
Ψ2, la densité de probabilité, définit les formes et les tailles des orbitales électroniques.

.