Débit massique
Centre de recherche Glenn
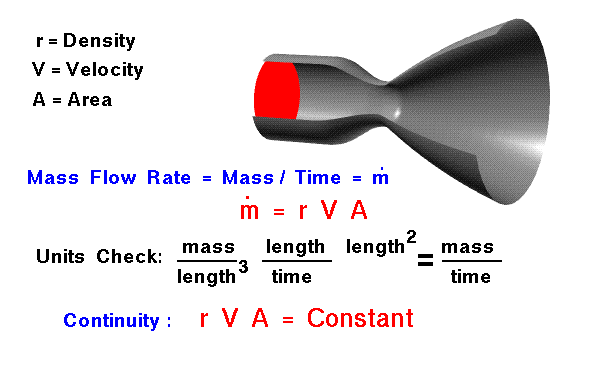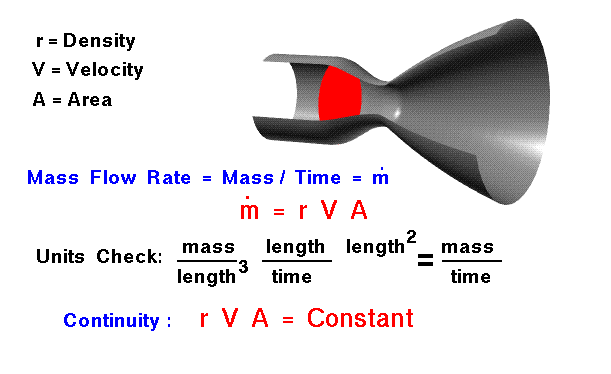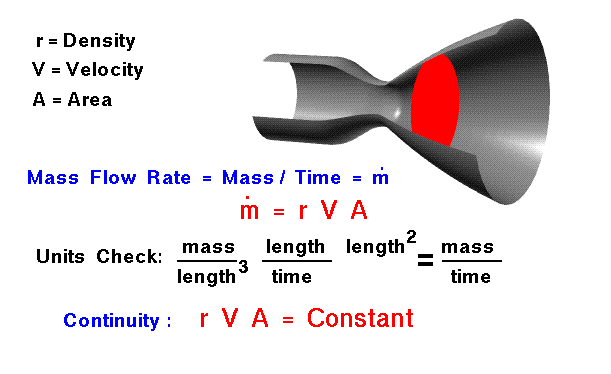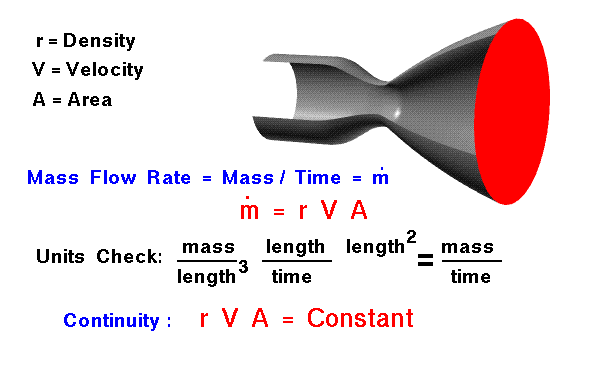
La conservation de la masse est un concept fondamental de la physique. Dans un certain domaine de problèmes, la quantité de masse reste constante – la masse n’est ni créée ni détruite. La masse d’un objet est simplement le volume occupé par l’objet multiplié par la densité de l’objet.Pour un fluide (un liquide ou un gaz), la densité, le volume et la forme de l’objet peuvent tous changer dans le domaine avec le temps. Et la masse peut se déplacer dans le domaine. Sur la figure, nous montrons un écoulement de gaz dans un tube rétréci. Il n’y a pas d’accumulation ou de destruction de masse dans le tube ; la même quantité de masse quitte le tube et y entre. A n’importe quel plan perpendiculaire à la ligne centrale du tube, la même quantité de masse passe à travers. Nous appelons la quantité de masse qui passe à travers une planète le débit massique. La conservation de la masse (continuité) nous dit que le débit massique à travers un tube est constant. Nous pouvons déterminer la valeur du débit massique à partir des conditions d’écoulement.
Si le fluide traverse initialement une zone A à la vitesse V,nous pouvons définir un volume de masse à balayer en un certain tempset. Le volume v est :
v = A * V * t
Un contrôle des unités donne aire xlongueur/temps x temps = aire x longueur = volume. La masse m contenue dans ce volume est simplement la densité r fois le volume.
m = r * A * V * t
Pour déterminer le débit massique mdot, on divise la masse par le temps. La définition du débit massique qui en résulte est indiquée en rouge sur la diapositive.
mdot = r * A * V
Comment les ingénieurs utilisent-ils cette connaissance du débit massique ? D’après la deuxième loi du mouvement deNewton, les forces aérodynamiques sur un avion (portance et traînée) sont directement liées au changement de quantité de mouvement d’un gaz en fonction du temps. Le momentum étant défini comme le produit de la masse par la vitesse, on peut s’attendre à ce que les forces aérodynamiques dépendent du débit massique d’un objet. La poussée produite par un système de propulsion dépend également du changement de quantité de mouvement d’un gaz de travail. La poussée dépend directement du débit massique à travers le système de propulsion. Pour un écoulement dans un tube, le débit massique est une constante. Pour un écoulement à densité constante, si nous déterminons (ou fixons) la vitesse à un endroit connu, l’équation nous indique la valeur de la vitesse pour tout autre endroit. Si nous désirons une certaine vitesse, nous connaissons la zone que nous devons fournir pour obtenir cette vitesse. Cette information est utilisée dans la conception des tunnels à vent.
En considérant l’équation du débit massique, il semblerait que pour une zone donnée, nous puissions rendre le débit massique aussi grand que nous le voulons en fixant la vitesse très élevée. Cependant, dans les fluides réels, les effets de compressibilité limitent la vitesse à laquelle un flux peut être forcé à travers une zone donnée. S’il y a une légère constriction dans le tube, comme le montre le graphique de la buse, le nombre de Mach de l’écoulement à travers la constriction ne peut être supérieur à un. Ce phénomène est communément appelé étranglement de l’écoulement et les détails de la physique sont donnés sur une page considérant les débits massiques compressibles.
Activités :
.12e année Visites guidées
-
Équations de base de la dynamique des fluides : 
Navigation .
Page d’accueil du guide du débutant.