Nous avons présenté une vue microscopique de la réaction chimique entre l’oxygène et l’hydrogène. L’équation
représente le même événement en termes de symboles et de formules chimiques.
Nous avons également vu que les plantes forment du glucose à partir de CO2 et de H2O :
Mais comment un chimiste praticien peut-il savoir ce qui se passe à l’échelle microscopique ? Lorsqu’une réaction est observée pour la première fois, on sait peu de choses sur la nature microscopique des produits. Il est donc nécessaire de déterminer expérimentalement la composition et la formule d’une substance nouvellement synthétisée.
La première étape d’une telle procédure consiste généralement à séparer et à purifier les produits d’une réaction. Les produits ci-dessus sont faciles à séparer, car ils sont liquides ou solides, alors que les réactifs sont gazeux. Mais comment avez-vous pu déterminer que la formule devait être H2O, et non H2O2 ? Les plantes produisent des mélanges d’hydrates de carbone pendant la photosynthèse, qui doivent être séparés par chromatographie ou d’autres techniques avant de pouvoir être identifiés. Le glucose est peut-être le sucre simple le plus courant, et il existe sous deux formes moléculaires, avec la formule chimique C6H12O6 :
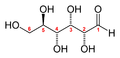
la forme à chaîne ouverte du glucose
la forme cyclique du glucose
Les plantes peuvent produire d’autres sucres simples avec des structures similaires, comme le D-ribulose (C5H10O5), le D-fructose (C6H12O6) et des di- ou polysaccharides (avec deux ou plusieurs sucres simples liés entre eux) comme le saccharose (C12H22O11) ou le maltose(C12H22O11).
Comment peut-on identifier le produit réel ?
Une réponse implique une analyse quantitative – la détermination du pourcentage en masse de chaque élément dans le composé. Ces données sont généralement rapportées sous forme de pourcentage de composition.
Exemple \(\PageIndex{1}\) : Composition en pourcentage
Lorsque 10,0 g d’oxygène réagissent avec suffisamment d’hydrogène, 11,26 g d’un composé pur sont formés. Calculez la composition en pourcentage à partir de ces données expérimentales.
Solution
Le pourcentage de dioxygène est la masse de dioxygène divisée par la masse totale du composé multipliée par 100 pour cent :
Le reste du composé (11.26 g – 10 g = 1,26 g) est de l’hydrogène:
\
À titre de contrôle, vérifier que la somme des pourcentages est égale à 100:
88,81% + 11.19% = 100%
Pour obtenir la formule à partir des données de composition en pourcentage, nous devons trouver combien d’atomes d’hydrogène il y a par atome d’oxygène. À l’échelle macroscopique, cela correspond au rapport entre la quantité d’hydrogène et la quantité d’oxygène. Si la formule est H2O, cela indique non seulement qu’il y a deux atomes d’hydrogène par atome d’oxygène, mais aussi qu’il y a 2 moles d’atomes d’hydrogène pour chaque 1 mole d’atomes d’oxygène. Autrement dit, la quantité d’hydrogène est deux fois supérieure à la quantité d’oxygène. Les chiffres du rapport entre la quantité de brome et la quantité de mercure (2:1) sont les indices d’hydrogène et d’oxygène dans la formule.
Exemple \(\PageIndex{2}\) : Détermination de la formule
Déterminer la formule du composé dont la composition en pourcentage a été calculée dans l’exemple précédent.
Solution
Par commodité, supposons que nous disposons de 100 g du composé. Sur cette quantité, 88,81 g (88,81 %) sont de l’oxygène et 11,19 g sont de l’hydrogène. Chaque masse peut être convertie en une quantité de substance
\begin{align}. & n_{\text{O}}=\text{88}\text{.81 g}\times \frac{\text{1 mol O}}{\text{16}\text{.00 g}=\text{5}\text{.550 mol O} \\\N & n_{\text{H}}=\text{11}\text{.19 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}=\text{11}\text{.101 mol H} \\\\N- \N-End{align}
Donc la formule est H11.101O5.550, mais nous savons qu’il n’y a pas de fractions d’atomes, donc nous devons mettre cela sous une forme standard. Pour ce faire, nous divisons la plus grande quantité par la plus petite:
Donc la formule est H1.998O1, mais là encore, il semble y avoir un problème. Le rapport 1,998 mol de H pour 1 mol de O implique également qu’il y a 1,998 atomes de H pour 1 atome de O. Si la théorie atomique est correcte, l’atome 0,998 n’existe pas ; mais en se rappelant que nos mesures ne sont bonnes qu’à trois chiffres significatifs, nous arrondissons 1,998 à 2,00 et écrivons la formule sous la forme H2O.
Exemple \(\PageIndex{3}\) : Formule du composé
Un oxyde d’hydrogène a pour composition 94,07% O et 5,93% H. Trouvez sa formule.
Solution
Supposons à nouveau un échantillon de 100 g et calculons la quantité de chaque élément :
\begin{align} & n_{\text{O}}=\text{94}\text{.07 g}\times \frac{\text{1 mol O}}{\text{16}\text{.00 g}=\text{5}\text{.88 mol O} \\N & n_{\text{H}}=\text{5}\text{.93 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}=\text{5}\text{.88 mol H} \\\\\N- \N-End{align}
Le rapport est
\
Donc la formule est H5.88O5.88, ce qui est un rapport 1:1 dans la précision expérimentale. Nous attribuerions donc la formule HO.
La formule obtenue dans l’exemple 3 ne correspond à aucun des deux oxydes d’hydrogène dont nous avons déjà parlé. S’agit-il d’un troisième ? La réponse est non, car notre méthode ne peut déterminer que le rapport entre H et O. Le rapport 1:1 est identique à 2:2, et notre méthode donnera donc le même résultat pour HO ou H2O2 (ou H7O7, d’ailleurs, s’il existe). La formule déterminée par cette méthode est appelée formule empirique ou formule la plus simple. Parfois, comme dans le cas du peroxyde d’hydrogène, la formule empirique diffère de la composition moléculaire réelle, ou de la formule moléculaire. La détermination expérimentale de la masse moléculaire en plus du pourcentage de composition permet de calculer la formule moléculaire.
Exemple \(\PageIndex{4}\) : Formules empirique et moléculaire
Un composé dont la masse moléculaire est de 28 contient 85,6 % de C et 14,4 % de H. Déterminez ses formules empirique et moléculaire.
Solution
\begin{align} & n_{\text{C}}=\text{85}\text{.6 g}\times \frac{\text{1 mol C}{\text{12}\text{.01 g}}=\text{7}\text{.13 mol C} \\\N & n_{\text{H}}=\text{14}\text{.4 g}\times \frac{\text{1 mol H}{\text{1}\text{.008 g}=\text{14}\text{.3 mol H}
Donc la formule est C7.13H14.3, mais pour obtenir des indices intégraux on divise chacun par le plus petit : \
La formule empirique est donc CH2. La masse moléculaire correspondant à la formule empirique est
12,01 + 2 × 1,008 = 14,03
Puisque la masse moléculaire expérimentale est deux fois plus grande, tous les indices doivent être doublés et la formule moléculaire est C2H4.
Exemple \(\PageIndex{5}\) : Formule empirique
D-Xylose contient 40,0% de C, 6,71% de H et 53,29% de O. Quelle est sa formule empirique ?
Solution
\begin{align} & n_{\text{H}}=\text{6}\text{.71 g}\times \tfrac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{6}\text{.66 mol H} & n_{\text{C}}=\text{40}\text{.00 g}\times \frac{\1 mol C}{\text{12}\text{.01 g}=\text{3}\text{.33 mol C} \\N & n_{\text{O}}=\text{53}\text{.29 g}\times \frac{\1 mol O}{\text{16}\text{.00 g}=\text{3}\text{.33 mol O}
Donc la formule est C3.33H6.66O3.33, et en divisant les trois par la plus petite quantité de substance, on obtient CH2O.
\N-begin{align} & \frac{n_{\text{C}}{n_{O}}}=\frac{\text{3}\text{3}{\text{3}{.33 mol C}}{\text{3}{.33 mol O}}=\frac{\text{1}\text{. mol H}{\text{1 mol O}} \\N & \frac{n_{\text{H}}{{\text{O}}=\frac{\text{4}\{.44 mol H}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.00 mol H}{\text{1 mol O}}
Nous voyons maintenant d’où vient le nom des glucides. Ils ont tous des formules comme Cn(H2O)m, donc ils ressemblent tous à des hydrates (composés contenant de l’eau) de carbone. Le D-Xylose est en fait C5(H2O)5 ou C5H10O5, le Glucose est C6(H12O)6 ou C6H12O6, et le Sucrose est C12(H2O)11 ou C12H22O11.
Nous avons vu que l’erreur expérimentale peut donner des rapports molaires qui ne sont pas des unités exactes. Parfois, le rapport des quantités est plus éloigné d’un nombre entier que ne peut l’expliquer l’erreur expérimentale, comme dans l’exemple suivant.
Exemple \(\PageIndex{6}\) : Formule empirique de l’aspirine
L’aspirine contient 60,0% de C, 4,48% de H et 35,5% de O. Quelle est sa formule empirique ?
Solution
\begin{align} & n_{\text{H}}=\text{14}\text{.4 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{14}\text{.3 mol H} \\N & n_{\text{C}}=\text{85}\text{.6 g}\times \frac{\1 mol C}{\text{12}\text{.01 g}=\text{7}\text{.13 mol C} \\N & n_{\text{O}}=\text{35}\text{.5 g}\times \frac{\{{1 mol O}}{\text{16}\text{.00 g}=\text{2}\text{.22 mol O}
Diviser les trois par la plus petite quantité de substance
\begin{align} & \frac{n_{\text{C}}{n_{O}}}=\frac{\text{5}\text{.00 mol C}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.25 mol H}{\text{1 mol O}} & \frac{n_{\text{H}}{{{O}}}=\frac{\text{4}\{.44 mol H}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.00 mol H}{\text{1 mol O}} \\ Il est clair qu’il y a deux fois plus d’atomes de H que d’atomes de O, mais le rapport entre C et O n’est pas si évident. Nous devons convertir 2,25 en un rapport de petits nombres entiers. Cela peut être fait en changeant les chiffres après la virgule en une fraction. Dans ce cas, .25 devient ¼. Ainsi 2,25 = 2¼ = 9/4, et
Nous pouvons également écrire
Donc la formule empirique est C9H8O4.
Une fois que quelqu’un a déterminé une formule – empirique ou moléculaire – il est possible pour quelqu’un d’autre de faire le calcul inverse. Trouver la composition en pourcentage du poids à partir de la formule s’avère souvent très instructif, comme le montre l’exemple suivant.
Exemple \(\PageIndex{7}\) : Composition en pourcentage d’un sucre
Comme nous l’avons vu précédemment, tous les glucides ont la formule générale Cn(H2O)m. Tous les sucres simples ont la formule générale Cn(H2O)n, ils ont donc tous le même pourcentage de C, H et O.
a. Calculez le pourcentage de C dans le glucose. b. Montrez que le composé C8(H2O)4 ne peut pas être un sucre simple en calculant son pourcentage de composition.
Solution
a. C6(H2O)6 contient 6 mol de C, 12 mol de H et 6 mol de O. La masse molaire est donc
M = (6 x 12,011) + (12 x 1,008) + (6 x 16) = 180 g mol-1
Un échantillon de 1 mol pèserait 180,56 g. La masse de 6 mol de C qu’il contient est
\
Donc le pourcentage de C est
\
Les pourcentages de H et de O se calculent facilement comme
\begin{align}. & m_{\text{H}}=\text{12 mol H}\cdot=\frac{\text{1.008 g}{\text{1 mol H}}=\text{12.096 g}\\&\text{%H}= \frac{\text{12.096 g}{\text{180.56 g}}\cdot\text{100%}=\text{6.70%}\\& m_{\text{O}}=\text{6 mol O}\cdot=\frac{\text{16.00 g}{\text{1 mol O}=\text{96.00 g}\\& \text{%O}= \frac{\text{96.00 g}}{\text{180.56 g}\cdot\text{100%}=\text{53.17%}\\end{align}
Bien que cela ne soit pas strictement nécessaire pour répondre au problème, les deux derniers pourcentages permettent de vérifier les résultats. Le total 40,00 + 6,70% + 53,17% = 100,00% comme il se doit.
Notez que pour tout sucre simple,
peu importe le nombre de carbones qu’il contient (les sucres simples sont des trioses, C3H6O3, des tétroses, C4H8O4, des pentoses et des hexoses. Il en va de même pour le pourcentage de H et de O.
b. La masse molaire de C8(H2O)4 est de 168,15;
%C = x 100% = 57,14%, et non les 40% caractéristiques des sucres simples.
De même,
%H = x 100% = 4,80% et le pourcentage de O est de 38,06%.
From ChemPRIME : 2.11 : Formules et composition