Développement de la distribution de Boltzmann
Les méthodes statistiques deviennent un moyen plus précis d’étudier la nature lorsque le nombre de particules est important. On s’attend donc à ce que la description des vitesses des molécules dans un gaz soit en fait la distribution la plus probable, puisque nous avons affaire à des nombres de particules de l’ordre du nombre d’Avogadro. Mais cette distribution la plus probable (la distribution de Maxwell-Boltzmann) est soumise à des contraintes, à savoir que le nombre de particules est constant et que l’énergie totale est constante (conservation de l’énergie). Maximiser la distribution de probabilité soumise à ces contraintes est en général une tâche mathématique redoutable (voir Richtmyer, et al., par exemple). Une façon d’aborder la solution de manière plus intuitive est de traiter un exemple physique que nous connaissons – à savoir la physique d’une atmosphère sous l’influence de la gravité telle que reflétée dans la formule barométrique. Le traitement suivant suit le développement de Rohlf.
Dans cette approche, nous utilisons le fait que l’énergie cinétique moyenne des molécules peut être exprimée en termes de température cinétique. De plus, nous savons que la conservation de l’énergie dans ce cas implique juste l’équilibrage de l’énergie cinétique et de l’énergie potentielle gravitationnelle tant que nous traitons l’atmosphère comme un gaz idéal.
À partir de l’expression de la température cinétique
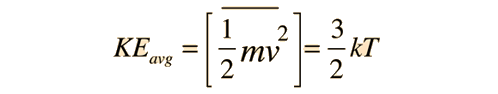
nous avons une expression testée expérimentalement pour l’énergie cinétique moléculaire. Dans la formule barométrique :
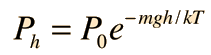
nous avons une description d’un système de gaz idéal qui peut être utilisée pour aider à développer un argument de plausibilité pour la distribution de vitesse de Maxwell. Les étapes de ce processus sont les suivantes :
Reliez la vitesse des particules à la hauteur.
Reliez le flux de particules à la distribution de vitesse.
Reliez la distribution de vitesse à la formule barométrique.
Calculez la distribution de vitesse et normalisez-la.
Pour une direction dans l’espace, ce processus donne l’expression :

et lorsque toutes les directions de vitesse sont incluses, elle devient la relation de distribution de vitesse de Maxwell :
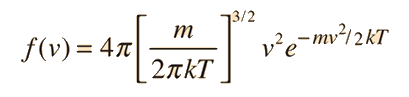 |
Pourquoi cette relation est-elle biaisée vers les vitesses plus élevées alors que celle qui précède directement ne l’est pas ? |
Il faut noter que bien que nous ayons utilisé une situation physique dépendant de la gravité pour obtenir la distribution des vitesses, la gravité n’apparaît pas dans le résultat final. C’est-à-dire que le résultat obtenu est un résultat général, ne contenant pas g. La formule barométrique a simplement été utilisée comme une construction pour relier la distribution de vitesse aux contraintes d’énergie et de nombre de particules.
.