Différents types d’angles existent dans la nature, et chacun d’entre eux porte une grande importance dans notre vie quotidienne.
Par exemple, les architectes et les ingénieurs utilisent des angles pour concevoir des machines, des bâtiments, des routes et des ponts.
Dans les sports, les athlètes utilisent des angles pour améliorer leurs performances. Par exemple, une personne doit tourner avec le disque selon un certain angle pour le lancer loin au lancer court. Au football, vous devez utiliser un certain angle pour passer le ballon au joueur suivant.
Les charpentiers et les artisans utilisent également des angles pour fabriquer des objets tels que des canapés, des tables, des chaises, des seaux, etc. Les artistes utilisent des angles pour esquisser des portraits et des peintures. Les créateurs de mode utilisent également des angles pour venir avec certains avec les meilleures tenues. Pour ces raisons, il est, donc, nécessaire que nous apprenions les différents types d’angles.
(Pour parcourir l’explication de base des angles, vous pouvez consulter l’article précédent, « Angles. »)
Différents types d’angles
Les angles sont classés en fonction de :
- Magnitude
- Rotation
Classification des angles en fonction de leur magnitude
Il existe sept types d’angles en fonction de leur mesure en degrés. Ils comprennent :
- Angles nuls
- Angles aigus
- Angles droits
- Obtus
- Angles droits
- Reflexes
- Angle complet
.
Angle nul
Un angle nul (0°) est un angle formé lorsque les deux bras de l’angle sont dans la même position.
Illustration :

∠ RPQ = 0° (angle nul)
Angle aigu
Un angle aigu est un angle supérieur à 0° mais inférieur à 90°. Les exemples courants d’angles aigus sont : 15°, 30°, 45°, 60°, etc.
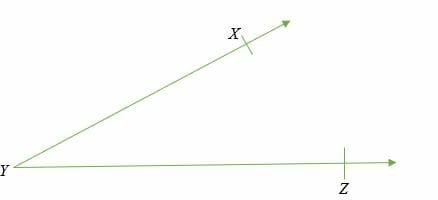
∠ XYZ est supérieur à 0° mais inférieur à 90° (angle aigu)
Angle à 90 degrés
Un angle à 90 degrés, également appelé angle droit, est un angle dont la mesure est égale à 90° est appelé angle droit. Les angles droits sont représentés en dessinant une petite boîte carrée entre les bras d’un angle.
Illustration:
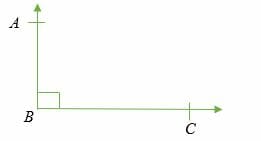
∠ ABC = 90° (angle droit)
Il y aura tout un article sur les triangles droits dans la section suivante (des Triangles).
Angle obtus
Un angle obtus est un type d’angle dont la mesure en degrés est supérieure à 90° mais inférieure à 180°. Des exemples d’angles obtus sont : 100°, 120°, 140°, 160°, 170°, etc.

∠ PQR est un angle obtus car il est inférieur à 180° et supérieur à 90°.
Angle droit
Comme son nom l’indique, un angle droit est un angle dont la mesure est égale à 180° (ligne droite)
Illustration :

∠ XYZ =180° (angle droit)
Angle réflexe
Les angles réflexes sont les types d’angles dont la mesure en degrés est supérieure à 180° mais inférieure à 360°. Les exemples courants d’angles réflexes sont ; 200°, 220°, 250°, 300°, 350°, etc.
Illustration:

∠ PQR est supérieur à 180° mais inférieur à 360°
Angle complet
Un angle complet est égal à 360°. 1 révolution est égale à 360°.
Illustration:
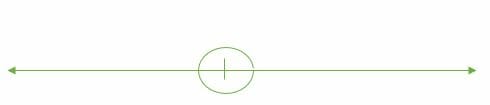
Classification des angles sur la base de la rotation
Selon le sens de rotation, les angles peuvent être classés en deux catégories, à savoir ;
- Angles positifs
- Angles négatifs
Angles positifs
Les angles positifs sont les types d’angles dont les mesures sont prises dans le sens inverse des aiguilles d’une montre à partir de la base.
Angles négatifs
Les angles négatifs sont des types d’angles dont les mesures sont prises dans le sens des aiguilles d’une montre à partir de la base.
Autres types d’angles
En dehors des angles évoqués ci-dessus, il existe d’autres types d’angles appelés angles paires. Ils sont appelés angles paires car ils apparaissent par paires pour montrer une certaine propriété. Ce sont :
- Des angles adjacents ont le même sommet et le même bras.
- Des angles complémentaires : Paire d’angles dont la somme est égale à 90º.
- Angles complémentaires : Paire d’angles dont la somme des angles est égale à 180º.
- Angles verticalement opposés . Les angles verticalement opposés sont égaux.
- Angles intérieurs alternés : Les angles intérieurs alternés sont des angles paires formés lorsqu’une ligne coupe deux lignes parallèles. Les angles intérieurs alternés sont toujours égaux entre eux.
- Angles extérieurs alternés : Les angles extérieurs alternés sont simplement des angles verticaux des angles intérieurs alternés. Les angles extérieurs alternés sont équivalents.
- Angles correspondants : Les angles correspondants sont des angles de paires formés lorsqu’une ligne intersecte une paire de lignes parallèles. Les angles correspondants sont également égaux entre eux.
Nous avons vu un bref aperçu des différents types d’angles. Ensuite, nous verrons les articles détaillés sur les types d’angles les plus courants (Angles complémentaires, Angles supplémentaires, etc.).