Un test t est un test statistique qui est utilisé pour comparer les moyennes de deux groupes. Il est souvent utilisé dans les tests d’hypothèses pour déterminer si un processus ou un traitement a réellement un effet sur la population d’intérêt, ou si deux groupes sont différents l’un de l’autre.
Vous voulez savoir si la longueur moyenne des pétales des fleurs d’iris diffère selon leur espèce. Vous trouvez deux espèces différentes d’iris poussant dans un jardin et mesurez 25 pétales de chaque espèce. Vous pouvez tester la différence entre ces deux groupes à l’aide d’un test t.
- L’hypothèse nulle (H0) est que la vraie différence entre ces moyennes de groupe est nulle.
- L’hypothèse alternative (Ha) est que la vraie différence est différente de zéro.
Quand utiliser un test t
Un test t ne peut être utilisé que pour comparer les moyennes de deux groupes (alias comparaison par paire). Si vous voulez comparer plus de deux groupes, ou si vous voulez faire plusieurs comparaisons par paires, utilisez un test ANOVA ou un test post-hoc.
Le test t est un test paramétrique de différence, ce qui signifie qu’il fait les mêmes hypothèses sur vos données que les autres tests paramétriques. Le test t suppose que vos données :
- sont indépendantes
- sont (approximativement) normalement distribuées.
- ont une quantité similaire de variance au sein de chaque groupe comparé (alias. homogénéité de la variance)
Si vos données ne correspondent pas à ces hypothèses, vous pouvez essayer une alternative non paramétrique au test t, comme le test de Wilcoxon Signed-Rank pour les données à variances inégales.
Quel type de test t dois-je utiliser ?
Lorsque vous choisissez un test t, vous devez prendre en compte deux éléments : si les groupes comparés proviennent d’une seule population ou de deux populations différentes, et si vous voulez tester la différence dans une direction spécifique.
Test t à un échantillon, à deux échantillons ou par paires ?
- Si les groupes proviennent d’une seule population (par exemple, mesurer avant et après un traitement expérimental), effectuez un test t apparié.
- Si les groupes proviennent de deux populations différentes (par exemple, deux espèces différentes, ou des personnes de deux villes distinctes), effectuez un test t à deux échantillons (alias test t indépendant).
- Si un groupe est comparé à une valeur standard (par ex.par exemple, comparer l’acidité d’un liquide à un pH neutre de 7), effectuez un test t à un échantillon.
Test t unilatéral ou bilatéral ?
- Si vous vous souciez uniquement de savoir si les deux populations sont différentes l’une de l’autre, effectuez un test t bilatéral.
- Si vous voulez savoir si la moyenne d’une population est supérieure ou inférieure à l’autre, effectuez un test t unilatéral.
Dans votre test visant à déterminer si la longueur des pétales diffère selon les espèces :
- Vos observations proviennent de deux populations distinctes (espèces distinctes), vous effectuez donc un test t à deux échantillons.
- Vous ne vous souciez pas du sens de la différence, mais seulement de savoir s’il y a une différence, vous choisissez donc d’utiliser un test t bilatéral.
Exécution d’un test t-.test
Le test t permet d’estimer la véritable différence entre deux moyennes de groupe en utilisant le rapport entre la différence des moyennes de groupe et l’erreur standard groupée des deux groupes. Vous pouvez le calculer manuellement à l’aide d’une formule, ou utiliser un logiciel d’analyse statistique.
Formule du test t
La formule du test t à deux échantillons (alias le test t de Student) est présentée ci-dessous.
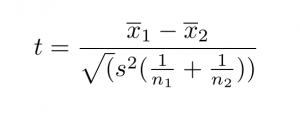
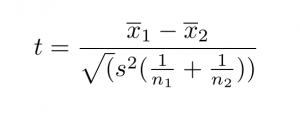
Dans cette formule, t est la valeur t, x1 et x2 sont les moyennes des deux groupes comparés, s2 est l’erreur standard regroupée des deux groupes, et n1 et n2 sont le nombre d’observations dans chacun des groupes.
Une valeur t plus grande montre que la différence entre les moyennes des groupes est supérieure à l’erreur standard regroupée, ce qui indique une différence plus significative entre les groupes.
Vous pouvez comparer votre valeur t calculée aux valeurs d’un tableau de valeurs critiques pour déterminer si votre valeur t est supérieure à ce qui serait attendu par hasard. Si c’est le cas, vous pouvez rejeter l’hypothèse nulle et conclure que les deux groupes sont en fait différents.
Fonction de test t dans les logiciels statistiques
La plupart des logiciels statistiques (R, SPSS, etc.) comprennent une fonction de test t. Cette fonction intégrée prendra vos données brutes et calculera la valeur t. Elle la comparera ensuite à la valeur critique, et calculera une valeur p. De cette façon, vous pouvez rapidement voir si vos groupes sont statistiquement différents.
Dans votre comparaison de la longueur des pétales de fleurs, vous décidez d’effectuer votre test t en utilisant R. Le code ressemble à ceci :
Téléchargez le jeu de données pour vous entraîner par vous-même.
Echantillon de données
Interprétation des résultats du test
Si vous effectuez le test t pour votre hypothèse sur les fleurs dans R, vous obtiendrez la sortie suivante :


La sortie fournit :
- Une explication de ce qui est comparé, appelé données dans le tableau de sortie.
- La valeur t : -33,719. Notez qu’elle est négative ; c’est très bien ! Dans la plupart des cas, nous ne nous soucions que de la valeur absolue de la différence, ou de la distance par rapport à 0. La direction n’a pas d’importance.
- Les degrés de liberté : 30,196. Les degrés de liberté sont liés à la taille de votre échantillon, et montrent combien de points de données » libres » sont disponibles dans votre test pour effectuer des comparaisons. Plus le nombre de degrés de liberté est élevé, plus votre test statistique sera efficace.
- La valeur p : 2,2e-16 (c’est-à-dire 2,2 avec 15 zéros devant). Cela décrit la probabilité que vous voyiez une valeur t aussi grande que celle-ci par hasard.
- Un énoncé de l’hypothèse alternative (Ha). Dans ce test, l’Ha est que la différence n’est pas de 0.
- L’intervalle de confiance à 95 %. Il s’agit de la plage de nombres dans laquelle la vraie différence de moyennes se situera dans 95 % des cas. Cela peut être changé de 95% si vous voulez un intervalle plus grand ou plus petit, mais 95% est très couramment utilisé.
- La longueur moyenne des pétales pour chaque groupe.
Présentation des résultats d’un test t
Lorsque vous présentez les résultats de votre test t, les valeurs les plus importantes à inclure sont la valeur t, la valeur p et les degrés de liberté du test. Celles-ci communiqueront à votre public si la différence entre les deux groupes est statistiquement significative (c’est-à-dire qu’il est peu probable qu’elle soit le fruit du hasard).
Vous pouvez également inclure les statistiques sommaires des groupes comparés, à savoir la moyenne et l’écart-type. En R, le code permettant de calculer la moyenne et l’écart type à partir des données ressemble à ceci :
Fleur.data %>%
group_by(Species) %>%
summarize(mean_length = mean(Petal.Length),
sd_length = sd(Petal.Length))
Dans notre exemple, vous rapporteriez les résultats comme suit :
Questions fréquemment posées sur les tests t
Un test t est un test statistique qui compare les moyennes de deux échantillons. Il est utilisé dans les tests d’hypothèses, avec une hypothèse nulle selon laquelle la différence entre les moyennes des groupes est nulle et une hypothèse alternative selon laquelle la différence entre les moyennes des groupes est différente de zéro.
Un test t mesure la différence des moyennes de groupe divisée par l’erreur standard regroupée des deux moyennes de groupe.
De cette façon, il calcule un nombre (la valeur t) illustrant l’ampleur de la différence entre les deux moyennes de groupe comparées, et estime la probabilité que cette différence existe purement par hasard (valeur p).
Votre choix de test t dépend du fait que vous étudiez un groupe ou deux groupes, et que vous vous souciez ou non du sens de la différence entre les moyennes des groupes.
Si vous étudiez un groupe, utilisez un test t apparié pour comparer la moyenne du groupe dans le temps ou après une intervention, ou utilisez un test t à un échantillon pour comparer la moyenne du groupe à une valeur standard. Si vous étudiez deux groupes, utilisez un test t à deux échantillons.
Si vous voulez seulement savoir si une différence existe, utilisez un test bilatéral. Si vous voulez savoir si la moyenne d’un groupe est supérieure ou inférieure à l’autre, utilisez un test unilatéral à gauche ou à droite.
Un test t à un échantillon est utilisé pour comparer une population unique à une valeur standard (par exemple, pour déterminer si la durée de vie moyenne d’une ville spécifique est différente de la moyenne du pays).
Un test t apparié est utilisé pour comparer une population unique avant et après une certaine intervention expérimentale ou à deux moments différents (par exemple, mesurer les performances d’un élève à un test avant et après qu’on lui ait enseigné la matière).
Un test t ne devrait pas être utilisé pour mesurer les différences entre plus de deux groupes, car la structure d’erreur d’un test t sous-estime l’erreur réelle lorsque de nombreux groupes sont comparés.
Si vous voulez comparer les moyennes de plusieurs groupes à la fois, il est préférable d’utiliser un autre test statistique tel que l’ANOVA ou un test post-hoc.
.
