Grado de elevación

• Cómo calcular la cota de elevación
• Cómo fijar las estacas de cota

Tienda de banderas de estacas a la venta de Johnson Level.

¿Qué es el grado de elevación?

El grado de una característica física de un objeto, una forma del terreno o una línea (plano) se utiliza para indicar la pendiente de la cosa que se está midiendo. Las aplicaciones del grado incluyen características físicas como colinas, riberas de ríos y cañones y aspectos de construcción como carreteras, inclinación de tejados y paisajismo. En otras palabras, cómo encontrar el grado de elevación es una habilidad importante en muchas áreas.

El grado también se llama comúnmente inclinación o subida. Dependiendo del método utilizado para encontrar el grado de elevación, puede expresarse de diferentes maneras como decimal, porcentaje y grado.

Cómo calcular el grado de elevación

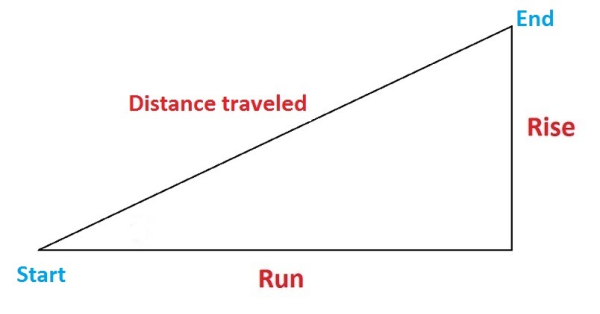
Antes de calcular el grado de elevación, se deben tomar las elevaciones de los puntos inicial y final para comparar, así como las distancias inicial y final. Tenga en cuenta que la distancia recorrida no es lo mismo que el «recorrido» (tratado en la siguiente sección). La «distancia recorrida» es la distancia atravesada entre los puntos inicial y final, no necesariamente la distancia «recorrida».

También asegúrese de que todas sus unidades son las mismas.

Como decimal

Una ecuación fácil de recordar para encontrar el cambio en la elevación como decimal es «ascenso sobre recorrido», lo que significa el ascenso (el cambio en la distancia vertical) dividido por el recorrido (el cambio en la distancia horizontal). Como ejemplo, digamos que la subida es 2 y el recorrido es 6. Entonces, tomarías 2 sobre 6 (o 2/6) para obtener 0,33 – ese es tu grado como decimal.



Como porcentaje

El proceso para medir la elevación como porcentaje es el mismo que para encontrar el cambio de elevación como decimal, con un paso extra. Entonces, encuentra la elevación sobre el recorrido. En nuestro ejemplo, es 2 sobre 6 (2/6) – esto es 0,33. Luego, simplemente multiplica el decimal por 100 para encontrar el porcentaje. En este caso, 33%. Un porcentaje positivo indica una pendiente ascendente. Un número positivo indica una pendiente ascendente, y viceversa.

En grados

En términos trigonométricos, el grado es la tangente del ángulo de una superficie que se mide a la horizontal. Cuanto mayor sea el número, mayor será el grado (o «inclinación»). En este caso, el grado se expresa en grados. Por ejemplo, el grado de elevación de una calle podría ser de 6,2°, lo que significa que la calle se inclina hacia arriba 6,2° desde la horizontal (el horizonte). En otras palabras, está viajando cuesta arriba.

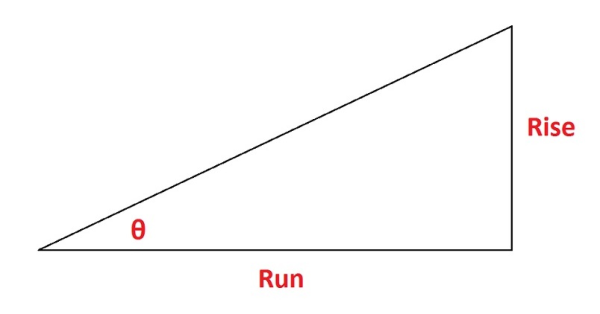
Al calcular la pendiente de elevación en grados, es útil pensar en el problema como un triángulo rectángulo. Utilizando la trigonometría básica, puede encontrar la pendiente en grados rápidamente. El siguiente diagrama muestra los tres aspectos básicos que necesitarás para hallar la pendiente.

Simplemente toma la «subida sobre el recorrido» y usa la arctangente (tan-1) para hallar theta (θ) – esa es tu pendiente en grados. Volviendo a nuestro ejemplo, la subida es 2 y el recorrido es 6. Por lo tanto, tomarías 2 sobre 6 (o 2/6) para obtener 0,33. Toma la arctangente de 0,33, que es 18,26. Por lo tanto, tu grado es de 18,26°. Un número positivo indica una pendiente ascendente, y viceversa.



Aplicación práctica de calcular y encontrar la pendiente de la elevación

La ecuación de la elevación sobre el recorrido puede aplicarse para establecer una nivelación sencilla para patios, caminos o entradas. Cada proyecto es diferente y no hay una única manera de establecer estacas de nivelación para todos y cada uno de los sitios de trabajo.

Aquí se muestra un ejemplo de nivelación de una pendiente simple en una dirección utilizando estacas de nivelación. Puede marcar cualquiera de las estacas como «corte» o «relleno» dependiendo del paisaje. En este ejemplo, describiremos un escenario en el que usted cortará la pendiente.

Cómo colocar las estacas de nivelación

1. Coloque estacas de nivelación en el suelo en cada extremo del área que necesita nivelar. La estaca en la parte superior de la pendiente se llama la bisagra. La estaca en la parte inferior de la pendiente se llama la punta.
2. Determine la pendiente deseada – normalmente 1-2% (1/8″ por pie a 1/4″ por pie) es suficiente para proporcionar suficiente escorrentía.
3. Ate una cuerda a una altura fija en la bisagra.
4. Corra la cuerda a través del sitio y átela en la punta tensa a la misma altura fija en la estaca.
5. Coloque un nivel de línea en la cuerda tensa. Mueva la cuerda desde el extremo de la puntera para que la cuerda quede nivelada.
6. Marque el lugar en el que la cuerda nivelada se une a la estaca. Digamos que para este ejemplo ha movido la cuerda hacia arriba 0,5″ (lo que significa que la caída actual es de 0,5″).
7. Suponga que la longitud entre las estacas es de 6 pies y que quiere una pendiente del 2%. 1/4″ x 6 = 1,5 pulgadas. Esto significa que quiere que la punta del pie esté 1,5 pulgadas por debajo de la bisagra.
8. La diferencia entre el grado deseado (1,5″) y el grado actual (0,5″) es lo que debe cortar de la estaca de la punta del pie.
9. En este caso, debe cavar hacia abajo 1″ desde la parte inferior del grado actual para alcanzar el grado deseado del 2%.

Compra banderas de estacas, disponibles en naranja y rojo, de Johnson Level and Tool.

Para más información o ayuda, consulte la colección de guías de cómo hacerlo de Johnson Level.

Cómo usar un tránsito para elevaciones

Cada ángulo está compuesto por el resultado de un conjunto de 3 puntos que se comparan. Los niveles de tránsito pueden utilizarse para ayudarte a averiguar el ángulo creado por un conjunto de tres objetos, y la distancia entre cada objeto en relación con los otros dos. Una vez que conozcas estas medidas, puedes introducir los números en las ecuaciones anteriores y calcular la pendiente.