Obiettivi di apprendimento
- utilizzare i grafici per analizzare la cinetica di una reazione.
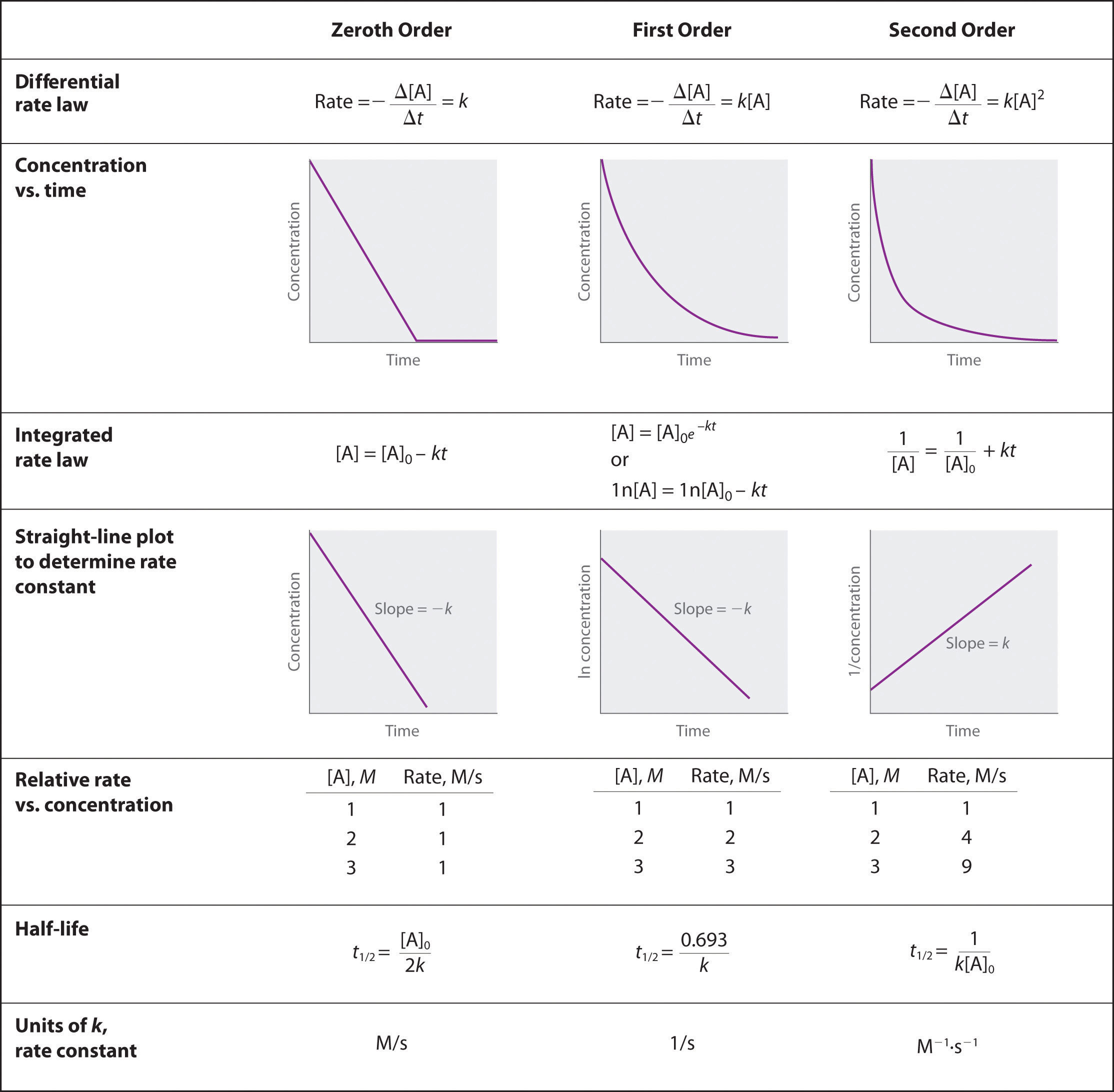
Hai imparato che la legge di velocità integrata per ogni tipo comune di reazione (zeroth, first, o second order in un singolo reagente) può essere tracciata come una linea retta. L’uso di questi grafici offre un’alternativa ai metodi descritti per mostrare come la concentrazione del reagente cambia con il tempo e determinare l’ordine della reazione. Illustreremo l’uso di questi grafici considerando la decomposizione termica del gas NO2 a temperature elevate, che avviene secondo la seguente reazione:
I dati sperimentali per questa reazione a 330°C sono elencati nella tabella \(\PageIndex{1}\); sono forniti come , ln, e 1/ rispetto al tempo per corrispondere alle leggi di velocità integrate per le reazioni di zerot-, primo e secondo ordine, rispettivamente.
| Tempo (s) | (M) | ln | 1/ (M-1) |
|---|---|---|---|
| 0 | 1.00 × 10-2 | -4.605 | 100 |
| 60 | 6.83 × 10-3 | -4.986 | 146 |
| 120 | 5.18 × 10-3 | -5.263 | 193 |
| 180 | 4.18 × 10-3 | -5.477 | 239 |
| 240 | 3.50 × 10-3 | -5.655 | 286 |
| 300 | 3.01 × 10-3 | -5.806 | 332 |
| 360 | 2.64 × 10-3 | -5.937 | 379 |
Le concentrazioni effettive di NO2 sono tracciate in funzione del tempo nella parte (a) della figura \(\PageIndex{1}\). Poiché il grafico di versus t non è una linea retta, sappiamo che la reazione non è di ordine zerotico in NO2. Un grafico di ln rispetto a t (parte (b) nella figura \(\PageIndex{1}}) ci mostra che la reazione non è di primo ordine in NO2 perché una reazione di primo ordine darebbe una linea retta. Avendo eliminato il comportamento dello zerot-ordine e del primo ordine, costruiamo un grafico di 1/ rispetto a t (parte (c) nella figura \(\PageIndex{1}}). Questo grafico è una linea retta, che indica che la reazione è del secondo ordine in NO2.
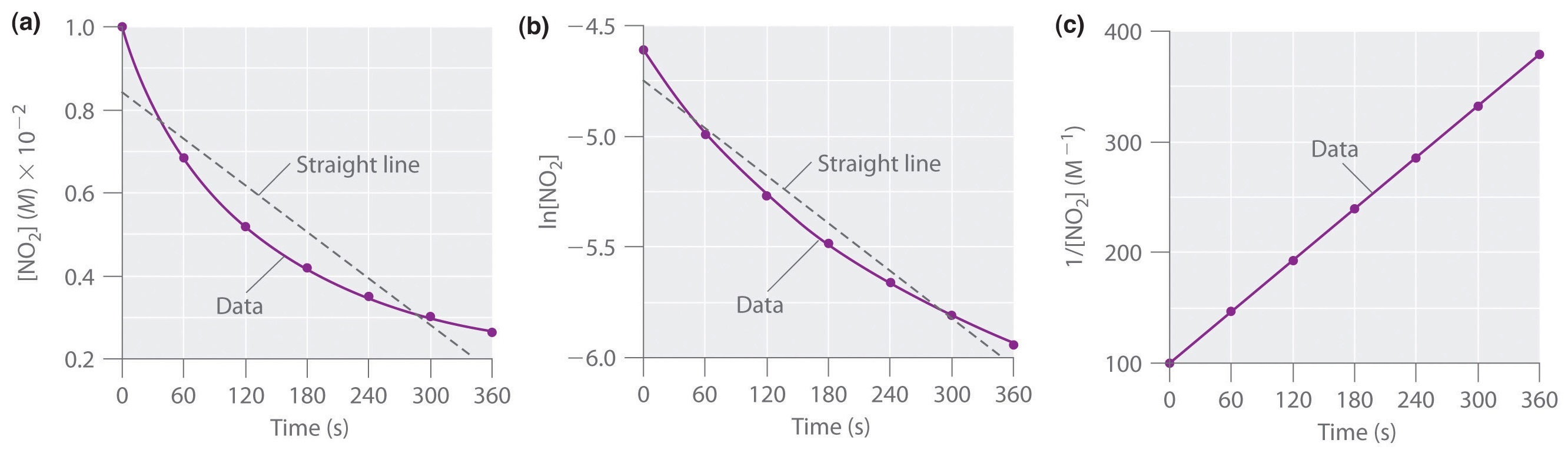
Abbiamo appena determinato l’ordine di reazione usando dati di un singolo esperimento tracciando la concentrazione del reagente in funzione del tempo. A causa delle forme caratteristiche delle linee mostrate nella figura \(\PageIndex{2}}), i grafici possono essere usati per determinare l’ordine di reazione di una reazione sconosciuta. Al contrario, il metodo dei tassi iniziali richiedeva esperimenti multipli a diverse concentrazioni di NO2 così come accurati tassi iniziali di reazione, che possono essere difficili da ottenere per reazioni rapide.
Esempio \(\PageIndex{1})
Il pentossido di azoto (N2O5) si decompone in NO2 e O2 a temperature relativamente basse nella seguente reazione:
Questa reazione si svolge in una soluzione di CCl4 a 45°C. Le concentrazioni di N2O5 in funzione del tempo sono elencate nella seguente tabella, insieme ai logaritmi naturali e alle concentrazioni reciproche di N2O5. Traccia un grafico della concentrazione rispetto a t, della concentrazione ln rispetto a t, e di 1/concentrazione rispetto a t e poi determina la legge di velocità e calcola la costante di velocità.
| Tempo (s) | (M) | ln | 1/ (M-1) |
|---|---|---|---|
| 0 | 0.0365 | -3.310 | 27.4 |
| 600 | 0.0274 | -3.597 | 36.5 |
| 1200 | 0.0206 | -3.882 | 48.5 |
| 1800 | 0.0157 | -4.154 | 63.7 |
| 2400 | 0.0117 | -4.448 | 85.5 |
| 3000 | 0.00860 | -4.756 | 116 |
| 3600 | 0.00640 | -5.051 | 156 |
Data: equazione chimica bilanciata, tempi di reazione e concentrazioni
Richiesto: grafico dei dati, legge della velocità e costante di velocità
Strategia:
A Usa i dati della tabella per tracciare separatamente la concentrazione, il logaritmo naturale della concentrazione e il reciproco della concentrazione (asse verticale) rispetto al tempo (asse orizzontale). Confronta i grafici con quelli della figura \(\PageIndex{1}} per determinare l’ordine di reazione.
B Scrivi la legge di velocità per la reazione. Usando i dati appropriati dalla tabella e il grafico lineare corrispondente alla legge di velocità per la reazione, calcola la pendenza della linea tracciata per ottenere la costante di velocità per la reazione.
Soluzione
A Ecco i grafici di versus t, ln versus t, e 1/ versus t:
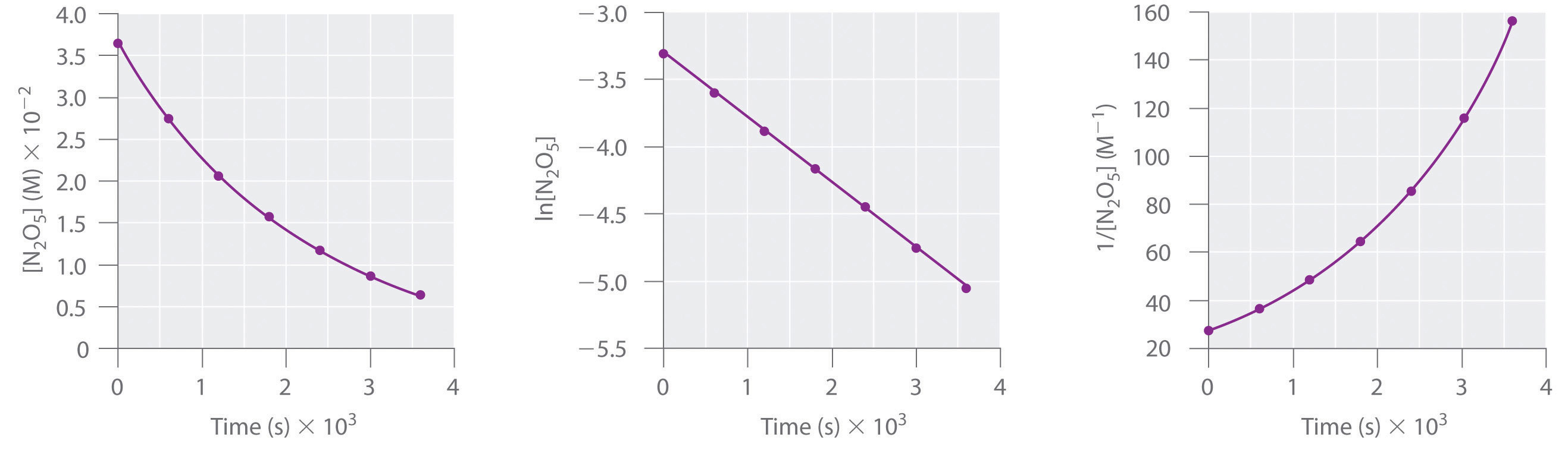
Il grafico di ln versus t dà una linea retta, mentre i grafici di versus t e 1/ versus t no. Questo significa che la decomposizione di N2O5 è del primo ordine in .
B La legge di velocità per la reazione è quindi
rate = k
Calcolare la costante di velocità è semplice perché sappiamo che la pendenza del grafico di ln contro t per una reazione del primo ordine è -k. Possiamo calcolare la pendenza usando due punti qualsiasi che si trovano sulla linea nel grafico di ln rispetto a t. Usando i punti per t = 0 e 3000 s,
Quindi k = 4,820 × 10-4 s-1.
Esercitazione \(\PageIndex{1})
1,3-Butadiene (CH2=CH-CH=CH2; C4H6) è una molecola organica volatile e reattiva usata nella produzione della gomma. Al di sopra della temperatura ambiente, reagisce lentamente per formare prodotti. Le concentrazioni di C4H6 in funzione del tempo a 326°C sono elencate nella seguente tabella insieme a ln e alle concentrazioni reciproche. Traccia un grafico dei dati come concentrazione contro t, concentrazione ln contro t, e 1/concentrazione contro t. Poi determina l’ordine di reazione nel C4H6, la legge di velocità e la costante di velocità per la reazione.
| Tempo (s) | (M) | ln | 1/ (M-1) |
|---|---|---|---|
| 0 | 1.72 × 10-2 | -4.063 | 58.1 |
| 900 | 1.43 × 10-2 | -4.247 | 69.9 |
| 1800 | 1,23 × 10-2 | -4,398 | 81.3 |
| 3600 | 9,52 × 10-3 | -4.654 | 105 |
| 6000 | 7.30 × 10-3 | -4.920 | 137 |
Risposta
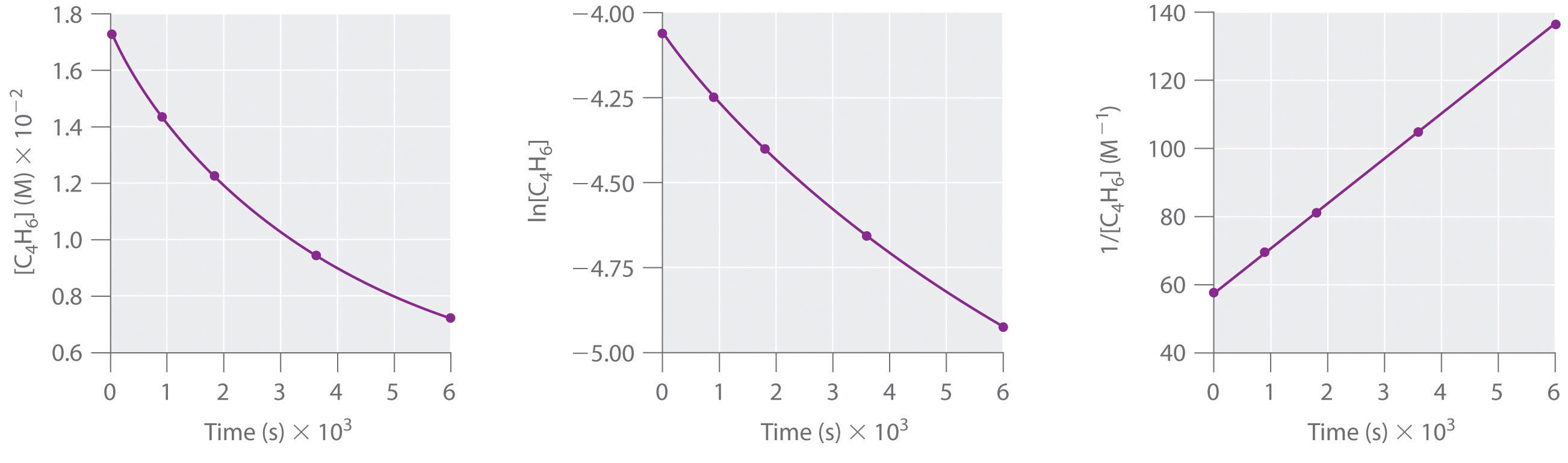
secondo ordine in C4H6; tasso = k2; k = 1,3 × 10-2 M-1-s-1
Sommario
Per una reazione di ordine zero, un grafico della concentrazione di qualsiasi reagente rispetto al tempo è una linea retta con una pendenza di -k. Per una reazione del primo ordine, un grafico del logaritmo naturale della concentrazione di un reagente rispetto al tempo è una linea retta con una pendenza di -k. Per una reazione del secondo ordine, il grafico dell’inverso della concentrazione di un reagente rispetto al tempo è una linea retta con una pendenza di k.