L’analisi dei fattori è una procedura statistica per descrivere le interrelazioni tra un numero di variabili osservate. L’analisi dei fattori è usata per misurare le variabili che non possono essere misurate direttamente, per riassumere grandi quantità di dati e per sviluppare e testare teorie. Ci sono due grandi categorie di analisi dei fattori: esplorativa e confermativa. Le tecniche di analisi fattoriale esplorativa hanno una storia molto più lunga delle tecniche di analisi fattoriale confermativa. Le differenze negli approcci portano ad usi diversi (per esempio, sviluppo della teoria contro conferma della teoria).
Scopi
L’analisi dei fattori ha tre scopi fondamentali. Primo, è utile per misurare costrutti che non possono essere facilmente osservati in natura. Per esempio, non possiamo sentire, vedere, annusare, gustare o toccare l’intelligenza, ma essa può essere dedotta dalla valutazione di variabili osservabili come le prestazioni in test di abilità specifiche. L’analisi dei fattori è anche utile nello sviluppo di scale per misurare gli atteggiamenti o altri costrutti latenti valutando le risposte a domande specifiche. In secondo luogo, l’analisi dei fattori è utile per riassumere una grande quantità di osservazioni in un numero più piccolo di fattori. Per esempio, esistono migliaia di descrittori di personalità nella lingua inglese. Attraverso l’analisi dei fattori, i ricercatori sono stati in grado di ridurre il numero di fattori distinti necessari per descrivere la struttura della personalità. In terzo luogo, l’analisi dei fattori è utile per fornire la prova della validità dei costrutti (per esempio, validità fattoriale, convergente e discriminante). Per esempio, se certe variabili osservabili sono teoricamente correlate tra loro, allora l’analisi dei fattori dovrebbe dimostrare queste relazioni teoriche, dimostrando simultaneamente che le stesse variabili sono ragionevolmente non correlate con le variabili di altri fattori latenti. Tutti e tre questi usi dell’analisi dei fattori possono essere impiegati nello sviluppo e nella verifica delle teorie psicologiche.
Modello Fattoriale di Base
Il problema dell’analisi dei fattori di base prende un numero di variabili osservabili e spiega le loro interrelazioni in un modo che è analogo a un’equazione di regressione. Il modello a fattori comuni è un’equazione di regressione in cui i fattori comuni agiscono come predittori delle variabili X osservate. Il modello fattoriale di base è rappresentato dall’equazione 1.
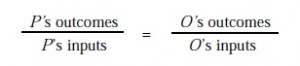
In questa equazione, X è la matrice delle variabili osservate, L è la matrice dei carichi dei fattori o pesi di regressione, f è la matrice dei fattori comuni, e u è la matrice dei residui. L’obiettivo è quello di spiegare le interrelazioni tra le variabili X attraverso i fattori comuni, f, e i termini di errore residui, chiamati unicità. La varianza in X è partizionata in componenti comuni e specifiche. A differenza della regressione, tuttavia, i predittori, f, sono sconosciuti.
Per fornire un esempio fittizio di questo problema, supponiamo che a un certo numero di supervisori venga chiesto di valutare l’importanza di sei caratteristiche di personalità per una prestazione lavorativa efficace da parte dei subordinati. Le caratteristiche valutate sono: organizzata, sistematica, disattenta, creativa,
intellettuale e immaginativa. La tabella 1 mostra la matrice di correlazione ipotetica per queste variabili. Il problema dell’analisi dei fattori è spiegare le relazioni tra queste variabili con meno di sei fattori latenti sottostanti. Organizzato, sistematico e disattento sono tutti correlati tra loro, ma non sono correlati con creativo, intellettuale e immaginativo. Allo stesso modo, creativo, intellettuale e immaginativo sono tutti correlati tra loro, ma non sono correlati con organizzato, sistematico e disattento. Ci sono due serie di correlazioni che riflettono due fattori sottostanti.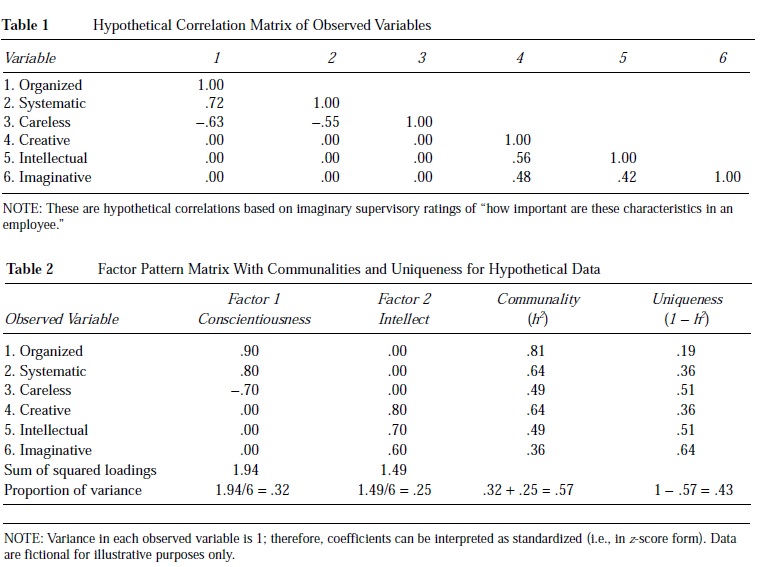
La tabella 2 mostra la matrice dei modelli dei fattori per queste variabili e i corrispondenti fattori latenti. I coefficienti del modello nella tabella 2 (colonne 2 e 3) sono le correlazioni delle variabili osservate con i fattori. Diverse matrici di pattern o di caricamento presenteranno diversi tipi di correlazioni (per esempio, correlazioni di Pearson, correlazioni parziali).
La comunanza (h2) nella colonna 4 della tabella 2 rappresenta la varianza che la variabile ha in comune con i fattori che rappresenta. La comunanza è analoga a una correlazione multipla al quadrato nella regressione. L’unicità nella colonna 5 rappresenta la varianza specifica di una variabile e non rappresentata dal fattore. L’unicità è analoga alla varianza residua nella variabile osservata dopo la contabilizzazione dei fattori. Le sei variabili fittizie rappresentano due fattori non osservabili, ogni fattore rappresenta dal 36% all’81% della varianza nelle variabili osservate.
In aggiunta alla varianza associata alle variabili osservate, la soluzione dell’analisi dei fattori descrive la varianza nei fattori stessi. La somma delle cariche quadrate (SSL) per un insieme di variabili descrive la varianza di ogni fattore. Prima che qualsiasi trasformazione nei carichi dei fattori abbia avuto luogo, questi SSL sono chiamati valori propri. Idealmente, un piccolo numero di fattori rappresenterà una grande quantità della varianza nelle variabili osservate. La tabella 2 mostra che i fattori rappresentano il 32% e il 25%, per un totale del 57% della varianza delle variabili osservate. Il restante 43% della varianza nelle variabili osservate non è comune ai fattori.
Analisi Fattoriale Esplorativa
Tipo, l’obiettivo dell’analisi fattoriale esplorativa (EFA) è quello di far determinare ai dati le interrelazioni tra un insieme di variabili. Anche se un ricercatore che usa l’EFA può avere una teoria che mette in relazione le variabili tra loro, ci sono relativamente poche restrizioni sul modello fattoriale di base in un EFA. Questo tipo di analisi è stato utile nello sviluppo della teoria e nel dibattito per più di un secolo.
L’analisi fattoriale esplorativa è particolarmente appropriata nelle prime fasi di sviluppo della teoria e nelle prime fasi di sviluppo della scala o del test. In primo luogo, l’EFA è utile nella riduzione dei dati quando le interrelazioni tra le variabili non sono specificate in anticipo. Un ricercatore che usa l’EFA fa uso del ragionamento induttivo prendendo un certo numero di osservazioni e sviluppando la teoria da quelle osservazioni. Nell’esempio delle caratteristiche dei dipendenti ad alte prestazioni, sei variabili di personalità sono state ridotte alla fine a due fattori. Per le analisi successive, quindi, è necessario discutere solo due variabili invece delle sei variabili originali. La riduzione dei dati è particolarmente utile per alleviare le preoccupazioni di multi-collinearità (correlazioni troppo elevate) tra un insieme di predittori. Un secondo vantaggio dell’EFA è la capacità di rilevare un fattore generale. Quando diversi test specifici di abilità cognitiva vengono analizzati, un fattore generale tende ad emergere, insieme a diversi fattori specifici. Nella valutazione dell’intelligenza, per esempio, tutti i test di abilità si correlano in qualche misura con il fattore generale dell’intelligenza, o g.
Infine, l’EFA è particolarmente utile nello sviluppo di scale o test perché permette al ricercatore di determinare la dimensionalità del test e rilevare i cross-loading (correlazioni di variabili con più di un fattore). I carichi incrociati non sono generalmente desiderabili. Nello sviluppo della scala, è vantaggioso avere item che si riferiscono ad un solo fattore. Per l’esempio precedente, le tre variabili che rappresentano la coscienziosità non si incrociano con l’intelletto e viceversa.
Analisi Fattoriale di Conferma
L’obiettivo dell’analisi fattoriale di conferma (CFA) è di testare le ipotesi teoricamente derivate da un insieme di dati. Il modello fattoriale di base dell’equazione 1 è ancora rilevante, ma alcune restrizioni sono imposte dal particolare modello teorico che viene testato. Per esempio, dall’esempio precedente, si potrebbe usare la CFA per imporre restrizioni sul modello dei fattori in modo che non siano permessi i cross-loading. Sviluppata negli anni ’60, la CFA è uno sviluppo statistico più recente dell’EFA (sviluppata nel 1904).
L’analisi fattoriale confermativa è particolarmente utile in un processo di ragionamento deduttivo. La verifica di ipotesi specifiche è possibile quando si usa la CFA. Per esempio, un ricercatore può affrontare la significatività statistica dei caricamenti dei singoli fattori. Nell’esempio precedente, data la correlazione relativamente piccola, si potrebbe determinare con certezza statistica il grado in cui la variabile osservata, immaginativa, è correlata al fattore latente, intelletto.
Con la CFA, è possibile testare l’ipotesi che due fattori contro un solo fattore (o qualsiasi altra combinazione numerica) siano alla base di un insieme di dati. In EFA, i ricercatori si affidano a regole empiriche e all’intuizione, che possono portare il ricercatore fuori strada, ma in CFA, i modelli possono essere esplicitamente confrontati attraverso test statistici di ipotesi nulla. Un altro uso della CFA è quello di valutare l’equivalenza di parti del modello fattoriale di base all’interno di un dato set di dati. Per esempio, si potrebbe ipotizzare che tutte le variabili osservate per l’intelletto siano ugualmente correlate all’intelletto. Con la CFA, l’equivalenza di queste relazioni può essere testata imponendo dei vincoli ai carichi nel modello fattoriale di base (cioè L nell’equazione 1).
È anche importante determinare se i risultati di un’analisi fattoriale sono simili tra gruppi demografici. L’analisi fattoriale confermativa permette di testare l’invarianza – cioè l’equivalenza della struttura dei fattori, i caricamenti, l’unicità – attraverso diversi gruppi (per esempio, etnici, di genere, culturali) di individui. Un ricercatore potrebbe essere interessato a sapere se la stessa ipotetica struttura di fattori emergerebbe se le risposte dei supervisori dei lavoratori manifatturieri fossero confrontate con le risposte dei supervisori dei lavoratori dei servizi. Potrebbe essere il caso che la variabile osservata non si riferisca ai fattori latenti nello stesso modo per i due gruppi. Per esempio, l’indicatore osservato sistematico può essere meno correlato al fattore coscienziosità per i lavoratori dei servizi che per i lavoratori manifatturieri. In una CFA che sta testando l’equivalenza dei caricamenti dei fattori, un ricercatore può testare l’ipotesi che le correlazioni dei due gruppi siano uguali o diverse.
L’analisi fattoriale confermativa ha una maggiore flessibilità di controllo rispetto all’EFA. Con la CFA, alcuni fattori possono essere specificati come obliqui (correlati tra loro), mentre altri sono specificati come ortogonali (non correlati tra loro). All’interno di una singola EFA, i fattori sono interpretati come obliqui o ortogonali ma non come una combinazione dei due. Inoltre, la CFA permette al ricercatore di imporre in modo flessibile vincoli aggiuntivi soggetti alla teoria (ad esempio, permettendo l’unicità correlata). Tuttavia, un vantaggio dell’EFA è che non sono necessari tali vincoli o specifiche teoriche. Pertanto, se non ne esistono, l’EFA può essere una scelta migliore.
- Gorsuch, R. L. (2003). Analisi dei fattori. In J. A. Schinka & W. F. Velicer (Eds.), Handbook of psychology: Metodi di ricerca in psicologia (Vol. 2, pp. 143-164). Hoboken, NJ: Wiley.
- Hurley, A. E., Scandura, T. A., Schriesheim, C. A., Brannick, M. T., Seers, A., Vandenberg, R. J., & Williams, L. J. (1997). Analisi dei fattori esplorativa e confermativa: Linee guida, problemi e alternative. Journal of Organizational Behavior, 18, 667-683.
- Lance, C. E., & Vandenberg, R. J. (2002). Analisi fattoriale confermativa. In F. Drasgow & N. Schmitt (Eds.), Misurare e analizzare il comportamento nelle organizzazioni: Advances in measurement and data analysis (pp. 221254). San Francisco: Jossey-Bass.
- Preacher, K. J., & MacCallum, R. C. (2003). Riparare la macchina elettrica per l’analisi dei fattori di Tom Swift. Understanding Statistics, 2, 13-43.
- Thompson, B. (2004). Analisi fattoriale esplorativa e confermativa: Capire i concetti e le applicazioni. Washington, DC: American Psychological Association.
- Vandenberg, R. J., & Lance, C. E. (2000). Una revisione e sintesi della letteratura sull’invarianza di misura: Suggerimenti, pratiche e raccomandazioni per la ricerca organizzativa. Organizational Research Methods, 3, 4-69.