Tolerance stacking, conosciuto anche come tolerance stack-up, si riferisce alla combinazione di varie tolleranze sulle dimensioni del pezzo. Dopo aver identificato una tolleranza sulla dimensione di un pezzo, è importante testare se quella tolleranza funzionerebbe con le tolleranze dell’utensile: o l’estremità superiore o quella inferiore. Un pezzo o un assemblaggio può essere soggetto a imprecisioni quando le sue tolleranze sono sovrapposte in modo scorretto.
L’importanza delle tolleranze
Le tolleranze influenzano direttamente il costo e le prestazioni di un prodotto. Tolleranze più strette rendono una parte lavorata più difficile da produrre e quindi spesso più costosa. Con questo in mente, è importante trovare un equilibrio tra la producibilità del pezzo, la sua funzionalità e il suo costo.
Suggerimenti per il successo dell’impilamento delle tolleranze
Evitare di usare tolleranze inutilmente piccole
Come detto sopra, le tolleranze più strette portano a un costo di produzione più alto perché il pezzo è più difficile da fare. Questo costo più elevato è spesso dovuto all’aumento della quantità di pezzi scartati che può verificarsi quando le dimensioni sono trovate fuori tolleranza. Il costo dei portautensili di alta qualità e degli utensili con tolleranze più strette può anche essere una spesa aggiuntiva.
Inoltre, tolleranze inutilmente piccole porteranno a tempi di produzione più lunghi, poiché ci sarà più lavoro per assicurare che il pezzo soddisfi criteri rigorosi durante la lavorazione e dopo la lavorazione nel processo di ispezione.
Fare attenzione a non sovradimensionare un pezzo
Quando una tolleranza superiore e inferiore è etichettata su ogni caratteristica di un pezzo, il sovradimensionamento può diventare un problema. Per esempio, una fresa a raggio d’angolo con un raggio d’angolo destro e sinistro potrebbe avere una tolleranza di +/- .001″, e il piano tra loro ha una tolleranza di .002″. In questo caso, la finestra di tolleranza per il diametro della fresa sarebbe +/- .004″, ma spesso viene calcolata male durante il dimensionamento del pezzo. Inoltre, mettere una tolleranza su questo callout causerebbe un sovradimensionamento, e quindi la quota di riferimento “REF” deve essere lasciata per prendere il posto della tolleranza.
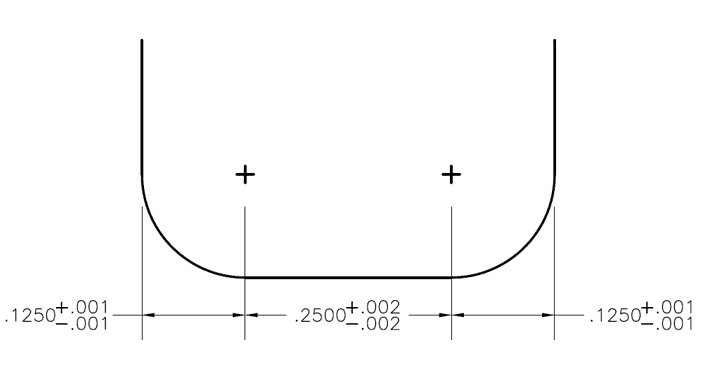
Figura 1: Forma della scanalatura creata da una fresa a raggio d’angolo
Utilizzare l’analisi statistica delle tolleranze:
L’analisi statistica guarda la probabilità che tutte e tre le tolleranze siano sotto o sopra la larghezza della scanalatura dimensionata, basata su una deviazione standard. Questa probabilità è rappresentata da una funzione di densità di probabilità normale, che può essere vista nella figura 2 qui sotto. Combinando tutte le probabilità delle diverse parti e dimensioni in un progetto, possiamo determinare la probabilità che una parte abbia un problema, o fallisca del tutto, in base alle dimensioni e alle tolleranze delle parti. Generalmente questo metodo di analisi è usato solo per assemblaggi con quattro o più tolleranze.
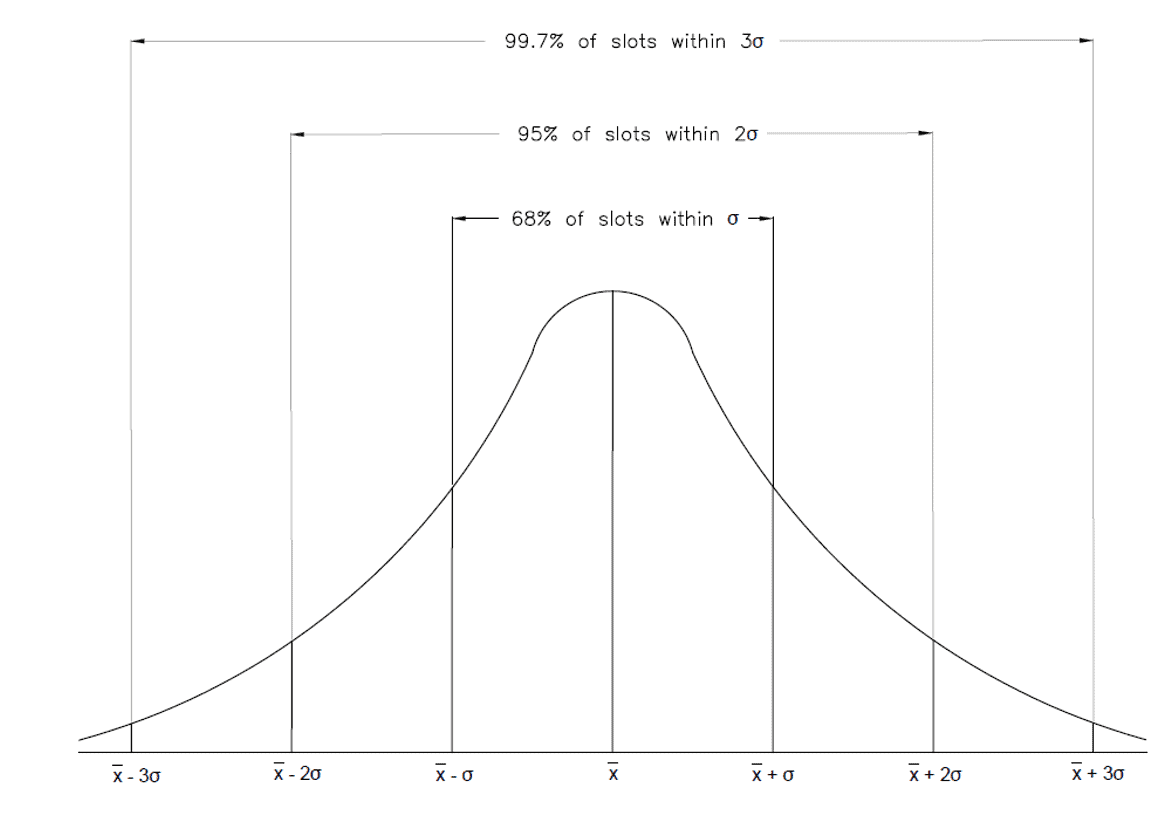
Figura 2: Impilamento delle tolleranze: Distribuzione normale
Prima di iniziare un’analisi statistica delle tolleranze, è necessario calcolare o scegliere un fattore di distribuzione delle tolleranze. La distribuzione standard è 3 . Questo significa che la maggior parte dei dati (o in questo caso delle tolleranze) saranno entro 3 deviazioni standard della media. Le deviazioni standard di tutte le tolleranze devono essere divise per questo fattore di distribuzione delle tolleranze per normalizzarle da una distribuzione di 3 a una distribuzione di 1. Una volta fatto questo, la somma delle radici al quadrato può essere presa per trovare la deviazione standard dell’insieme.
Pensate ad una tazza di caffè fatta con 3 chicchi di dimensioni diverse. Per fare una deliziosa tazza di caffè, devi prima macinare tutti i chicchi alla stessa dimensione in modo che possano essere aggiunti al filtro del caffè. In questo caso, i chicchi sono le deviazioni standard, il macinino è il fattore di distribuzione delle tolleranze e il filtro del caffè è l’equazione della somma quadratica delle radici. Questo è necessario perché alcune tolleranze possono avere diversi fattori di distribuzione in base alla ristrettezza dell’intervallo di tolleranza.
Il metodo di analisi statistica viene utilizzato se c’è un requisito che la fessura deve essere larga .500″ con una tolleranza di +/- .003″, ma non c’è bisogno che i raggi (.125″) e il piatto (.250″) siano esatti, purché si adattino alla fessura. In questo esempio, abbiamo 3 tolleranze bilaterali con le loro deviazioni standard già disponibili. Poiché sono bilaterali, la deviazione standard dalla media sarebbe semplicemente qualsiasi valore di tolleranza + o -. Per i raggi esterni, questo sarebbe .001″ e per la regione centrale piatta questo sarebbe .002″.
Per questo esempio, troviamo la deviazione standard (σ) di ogni sezione usando l’equazione 1. In questa equazione rappresenta la deviazione standard.
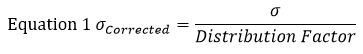
L’ipotesi standard è che la tolleranza di un pezzo rappresenti una distribuzione normale +/- 3. Pertanto, il fattore di distribuzione sarà 3. Usando l’equazione 1 sulla sezione sinistra della figura 1, troviamo che la sua deviazione standard corretta equivale a:
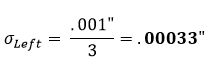
Questo viene poi ripetuto per le sezioni centrale e destra:
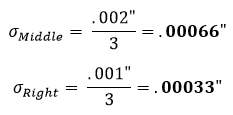
Dopo aver ottenuto queste deviazioni standard, inseriamo i risultati nell’equazione 2 per trovare la deviazione standard della zona di tolleranza. L’equazione 2 è conosciuta come l’equazione della somma delle radici al quadrato.
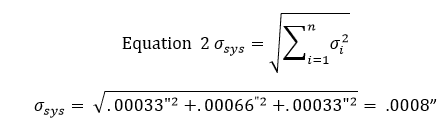
A questo punto, significa che il 68% delle scanalature sarà entro una tolleranza di +/- .0008″. Moltiplicando questa tolleranza per 2 si otterrà una finestra di confidenza del 95%, mentre moltiplicandola per 3 si otterrà una finestra di confidenza del 99%.
Il 68% degli slot sarà entro +/- .0008″
il 95% degli slot sarà compreso entro +/- .0016″
il 99% degli slot sarà compreso entro +/- .0024″
Queste finestre di confidenza sono standard per un insieme di punti dati distribuiti normalmente. Una distribuzione normale standard può essere vista nella figura 2 qui sopra.
L’analisi statistica delle tolleranze dovrebbe essere usata solo per assemblaggi con più di 4 parti con tolleranza. Molti fattori non sono stati presi in considerazione in questa semplice analisi. Questo esempio era per 3 dimensioni bilaterali le cui tolleranze erano rappresentative delle loro deviazioni standard dalle loro medie. Nell’analisi statistica standard delle tolleranze, entrano in gioco altre variabili come gli angoli, il runout e il parallelismo, che richiedono fattori di correzione.
Utilizzare l’analisi del caso peggiore:
L’analisi del caso peggiore è la pratica di sommare tutte le tolleranze di un pezzo per trovare la tolleranza totale del pezzo. Quando si esegue questo tipo di analisi, ogni tolleranza è impostata al suo limite più grande o più piccolo nel suo rispettivo intervallo. Questa tolleranza totale può poi essere confrontata con i limiti di prestazione della parte per assicurarsi che l’assemblaggio sia progettato correttamente. Questo è tipicamente usato per una sola dimensione (solo 1 piano, quindi nessun angolo coinvolto) e per assemblaggi con un piccolo numero di parti.
L’analisi del caso peggiore può anche essere usata quando si sceglie l’utensile da taglio appropriato per il vostro lavoro, poiché la tolleranza dell’utensile può essere aggiunta alla tolleranza della parte per uno scenario peggiore. Una volta che questo scenario è identificato, il macchinista o l’ingegnere può fare le regolazioni appropriate per mantenere il pezzo entro le dimensioni specificate sulla stampa. Va notato che lo scenario peggiore si verifica raramente nella produzione reale. Mentre queste analisi possono essere costose per la produzione, forniscono la pace della mente ai macchinisti garantendo che tutti gli assemblaggi funzioneranno correttamente. Spesso questo metodo richiede tolleranze strette perché l’impilamento totale alle condizioni massime è la caratteristica principale utilizzata nella progettazione. Tolleranze più strette intensificano i costi di produzione a causa dell’aumento della quantità di raschiatura, del tempo di produzione per l’ispezione e del costo delle attrezzature utilizzate su queste parti.
Esempio di scenario peggiore nel contesto della Figura 1:
Trova il limite inferiore di specifica.
Per il raggio dell’angolo sinistro
.125″ – .001″ = .124″
Per la sezione piatta
.250″ – .002″ = .248″
Per il raggio dell’angolo destro
.125″ – .001″ = .124″
Aggiungi tutti questi al limite inferiore delle specifiche:
.124″ + .248″ + .124″ = .496″
Trovare il limite superiore di specifica:
Per il raggio dell’angolo sinistro