Campo gravitazionale uniforme senza resistenza dell’ariaModifica
Questo è il caso “da manuale” del moto verticale di un oggetto che cade per una piccola distanza vicino alla superficie di un pianeta. È una buona approssimazione nell’aria finché la forza di gravità sull’oggetto è molto maggiore della forza di resistenza dell’aria, o equivalentemente la velocità dell’oggetto è sempre molto minore della velocità terminale (vedi sotto).
v ( t ) = v 0 + g t {\displaystyle v(t)=v_{0}+gt\,}
y ( t ) = v 0 t + y 0 + 1 2 g t 2 {displaystyle y(t)=v_{0}t+y_{0}+{frac {1}{2}}gt^{2}}
dove
v 0 {displaystyle v_{0},}
è la velocità iniziale (m/s). v ( t ) {displaystyle v(t)\,}
è la velocità verticale rispetto al tempo (m/s). y 0 {displaystyle y_{0},}
è la quota iniziale (m). y ( t ) {displaystyle y(t)\,}
è l’altitudine rispetto al tempo (m). t {displaystyle t\,}
è il tempo trascorso (s). g {displaystyle g\,}
è l’accelerazione dovuta alla gravità (9,81 m/s2 vicino alla superficie della terra).
Campo gravitazionale uniforme con resistenza dell’ariaModifica
Questo caso, che si applica ai paracadutisti, ai paracadutisti o a qualsiasi corpo di massa, m {\displaystyle m}
, e l’area della sezione trasversale, A {displaystyle A}
, con numero di Reynolds ben al di sopra del numero critico di Reynolds, in modo che la resistenza dell’aria sia proporzionale al quadrato della velocità di caduta, v {displaystyle v}
, ha un’equazione del moto m d v d t = m g – 1 2 ρ C D A v 2 , {displaystyle m{frac {mathrm {d} v}{mathrm {d} t}}=mg-{\frac {1}{2}}\rho C_{\mathrm {D}
dove ρ {displaystyle \rho }
è la densità dell’aria e C D {displaystyle C_{mathrm {D} }}
Assumendo un oggetto che cade da fermo e nessun cambiamento nella densità dell’aria con la quota, la soluzione è: v ( t ) = v ∞ tanh ( g t v ∞ ) , {displaystyle v(t)=v_{\\infty }tanh \left({\frac {gt}{v_{\infty}} a destra),
dove la velocità terminale è data da
v ∞ = 2 m g ρ C D A . {displaystyle v_{{infty }={sqrt {frac {2mg}{rho C_{D}A}}},.}
La velocità dell’oggetto rispetto al tempo può essere integrata nel tempo per trovare la posizione verticale in funzione del tempo:
y = y 0 – v ∞ 2 g ln cosh ( g t v ∞ ) . {displaystyle y=y_{0}-{frac {v_{infty}^{2}}{g}}ln \cosh \left({\frac {gt}{v_{infty}}destra).}
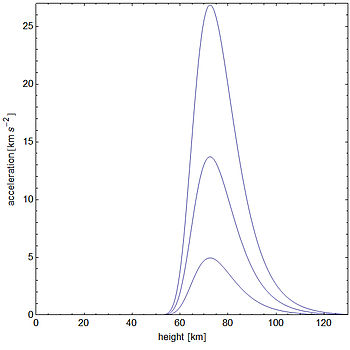
Utilizzando la cifra di 56 m/s per la velocità terminale di un uomo, si trova che dopo 10 secondi sarà caduto 348 metri e avrà raggiunto il 94% della velocità terminale, e dopo 12 secondi sarà caduto 455 metri e avrà raggiunto il 97% della velocità terminale. Tuttavia, quando la densità dell’aria non può essere assunta come costante, come per gli oggetti che cadono da altezze elevate, l’equazione del moto diventa molto più difficile da risolvere analiticamente e una simulazione numerica del moto è solitamente necessaria. La figura mostra le forze che agiscono sui meteoroidi che cadono attraverso l’atmosfera superiore della Terra. Anche i salti HALO, compresi i salti record di Joe Kittinger e Felix Baumgartner, appartengono a questa categoria.
Legge dell’inverso quadrato del campo gravitazionaleModifica
Si può dire che due oggetti nello spazio che orbitano l’uno attorno all’altro in assenza di altre forze sono in caduta libera l’uno attorno all’altro, ad esempio che la Luna o un satellite artificiale “cade attorno” alla Terra, o un pianeta “cade attorno” al Sole. Assumere oggetti sferici significa che l’equazione del moto è governata dalla legge di gravitazione universale di Newton, con soluzioni al problema gravitazionale a due corpi che sono orbite ellittiche che obbediscono alle leggi del moto planetario di Keplero. Questa connessione tra gli oggetti che cadono vicino alla Terra e gli oggetti orbitanti è meglio illustrata dall’esperimento del pensiero, la palla di cannone di Newton.
Il moto di due oggetti che si muovono radialmente uno verso l’altro senza momento angolare può essere considerato un caso speciale di un’orbita ellittica di eccentricità e = 1 (traiettoria ellittica radiale). Questo permette di calcolare il tempo di caduta libera per due oggetti puntiformi su un percorso radiale. La soluzione di questa equazione del moto fornisce il tempo in funzione della separazione:
t ( y ) = y 0 3 2 μ ( y y 0 ( 1 – y y 0 ) + arccos y y 0 ) , {displaystyle t(y)={sqrt {{frac {y_{0}}^{3}}{2\mu }}left({sqrt {{frac {y_{0}} a sinistra(1-{frac {y_{0}}} a destra)}+arccos {sqrt {y_{y_{0}}}}}} a destra),
dove
t {displaystyle t}
è il tempo dopo l’inizio della caduta y {\displaystyle y}
è la distanza tra i centri dei corpi y 0 {displaystyle y_{0}}
è il valore iniziale di y {\displaystyle y}
μ = G ( m 1 + m 2 ) {displaystyle \mu =G(m_{1}+m_{2})}
è il parametro gravitazionale standard.
Sostituendo y = 0 {displaystyle y=0}
otteniamo il tempo di caduta libera.
La separazione in funzione del tempo è data dall’inverso dell’equazione. L’inverso è rappresentato esattamente dalla serie di potenza analitica:
y ( t ) = ∑ n = 1 ∞ ) ] . {\displaystyle y(t)==somma _{n=1}^{infty\left)\destra].}
![{{displaystyle y(t)==sum _{n=1}^{infty }{left\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9efcee875e66a75503356d3f01a17710980518bb)
Valutando questo risultato si ottiene: