La quarta dimensione è un luogo in cui si può viaggiare andando in una direzione perpendicolare alla terza dimensione. Ad un occhio inesperto, questa affermazione non ha assolutamente senso. Come può esistere una direzione perpendicolare ad uno spazio tridimensionale? Per capire meglio questo concetto, dobbiamo farci strada lentamente attraverso tutte le dimensioni e analizzare quali cambiamenti avvengono tra una dimensione e l’altra.

Dimensione zero
La dimensione zero è quella a cui non pensiamo spesso. I punti sono gli unici esseri dimensionali che possono essere correttamente compresi nella dimensione zeroth. Non hanno assolutamente nessuna dimensione, nessuna larghezza, nessuna lunghezza, nessuna altezza. Sono i più piccoli che possano mai essere, ma anche i più grandi che possano mai essere allo stesso tempo.
Come cerchiamo di approfondire la nostra comprensione della quarta dimensione. Possiamo esaminare un cubo in ogni dimensione mentre procediamo. Un cubo nella dimensione zero sarebbe semplicemente un punto. Tutte le sue dimensioni sono le stesse in ogni direzione perché non ce ne sono. Il cubo rappresenta ancora un punto nello spazio, ma questo è il limite del suo potere nella dimensione zero. Ora, passiamo alla 1-D.
Prima dimensione
Il passaggio tra la dimensione zero e la prima dimensione comporta un’estrusione in qualsiasi direzione. Nella prima dimensione, tutto esiste come una linea. L’unica cosa che differisce tra gli oggetti nella prima dimensione è la loro lunghezza. Le linee hanno tutte la stessa larghezza e la stessa altezza, ma la loro lunghezza può essere variata.
Se vuoi fare linee di spessore variabile, allora devi passare a linee bidimensionali. Un cubo nella prima dimensione apparirebbe come una linea con la stessa lunghezza di detto cubo, ma senza valori di larghezza o altezza.
Seconda dimensione
Trasformando un segmento di linea in una direzione perpendicolare alla direzione 1-dimensionale si entra nella seconda dimensione. Tenete questa idea in mente mentre espandiamo la nostra conoscenza dimensionale e notate questa azione perpendicolare ripetuta mentre ci muoviamo attraverso le dimensioni.
Nella seconda dimensione, il nostro cubo può cominciare ad assomigliare ad un cubo, ma solo appena appena. Un cubo esisterebbe come un quadrato nella seconda dimensione. Si può, naturalmente, disegnare una rappresentazione di un cubo 3D in 2 dimensioni, ma non è quello che un cubo sembrerebbe in 2 dimensioni. Piuttosto questa sarebbe semplicemente una rappresentazione della terza dimensione sovrapposta alla seconda.
Lunghezza e larghezza possono essere variate nella seconda dimensione, il che permette forme e geometria di base. Quando ci spostiamo nella terza dimensione, la matematica inizia a diventare più complessa.
Terza dimensione
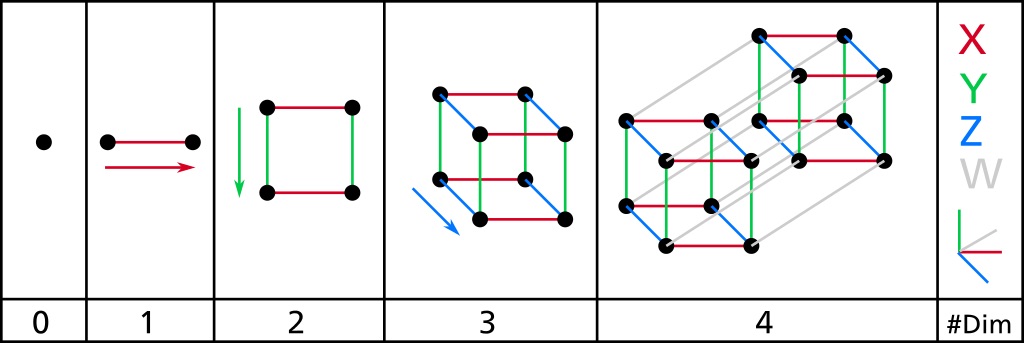
Il cubo della seconda dimensione viene ora estruso in una terza direzione perpendicolare a entrambi i lati del quadrato 2D. Per metterlo in termini cartesiani, il quadrato 2D esisteva nelle direzioni X e Y. Spostandoci nella terza dimensione abbiamo estruso quel quadrato nella direzione Z. La terza dimensione è dove il nostro cubo diventa effettivamente un cubo nel nostro senso tradizionale definito. L’oggetto ha dimensioni di larghezza, lunghezza e altezza.
In tutte le dimensioni, è importante notare che un cubo manterrà tutte le sue proprietà di base in teoria. Tutti gli angoli saranno retti e tutti i lati saranno uguali. Portando un altro principio di dimensioni, possiamo esaminare cosa accadrebbe se il cubo fosse espanso indefinitamente. Quando un cubo nella terza dimensione viene espanso all’infinito, ingloba la totalità dello spazio tridimensionale.
Finora, dovreste probabilmente afferrare queste 3 dimensioni, dopo tutto, sono le dimensioni che associamo più comunemente.
Quarta dimensione
Quando portiamo il cubo nella quarta dimensione, cominciamo a sperimentare una matematica controintuitiva. Estrudiamo il cubo in una direzione perpendicolare a tutte le prime tre. Questo è impossibile nella terza dimensione perché ci sono solo 3 dimensioni in cui il cubo è già espanso. Quando aggiungiamo la quarta dimensione, per mantenere le proprietà del cubo che tutti gli angoli sono di 90 gradi e tutti i lati sono uguali, dobbiamo estrudere in questa nuova dimensione.
I cubi nella quarta dimensione sono tecnicamente chiamati tesseratti. Gli oggetti in 4D differiscono in lunghezza, larghezza, altezza e forza. Sovrapponendo la resistenza a una qualsiasi delle dimensioni precedenti, un oggetto nelle dimensioni successive ha una resistenza pari a 0, o un valore infinitamente piccolo.
Tutti i bordi di un tesseratto sono uguali, e tutti gli angoli sono retti. Questo ha senso in teoria, ma quando cominciamo a immaginare l’aspetto di un tesseratto, siamo vincolati dalla nostra mente tridimensionale. Per vedere un tesseratto, dobbiamo sovrapporre questo oggetto di quarta dimensione alla terza dimensione.
Il modo principale con cui rappresentiamo un tesseratto, o un cubo di quarta dimensione, è proiettandolo nella terza dimensione con la prospettiva. Questa rappresentazione può essere vista qui sotto.
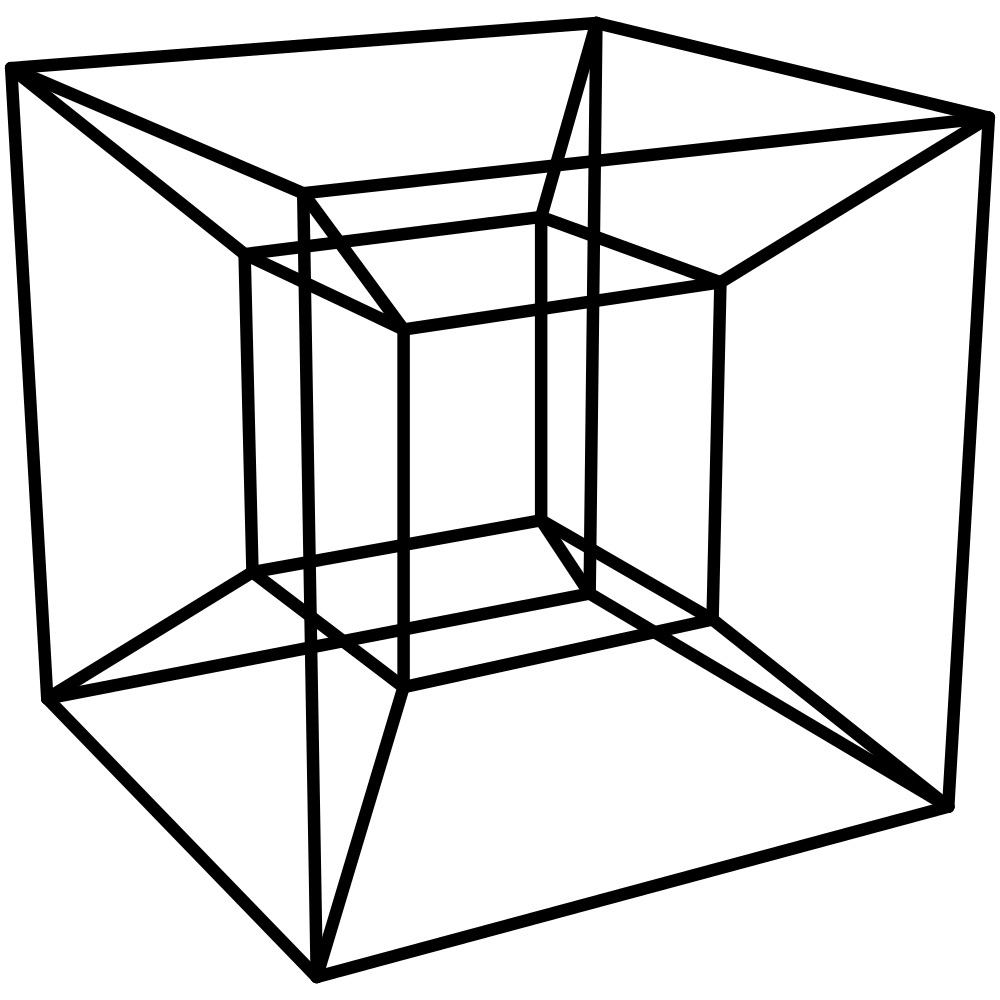
Questa è anche una rappresentazione prospettica di un tesseratto in forma di gif.

Questa rappresentazione non è come appare un cubo 4D, è semplicemente come appare in prospettiva visto dalla terza dimensione. Per riassumere la nostra comprensione della quarta dimensione, gli oggetti in 4D variano in valore per lunghezza, larghezza, altezza e forza. Tutte queste misure dimensionali si estendono in una direzione perpendicolare alle tre precedenti. La larghezza è perpendicolare alla lunghezza, l’altezza è perpendicolare alla larghezza e alla lunghezza, e infine la forza è perpendicolare all’altezza, alla lunghezza e alla larghezza.
Questi concetti sono difficili da afferrare, ma si spera che questo vi dia una buona comprensione generale di come funziona la quarta dimensione e come la interpretiamo dai nostri occhi tridimensionali.
Non ha ancora senso? Lasciate che Carl Sagan ve lo spieghi.