È possibile trasformare una funzione rimpicciolendola? Sì! Una delle tecniche di trasformazione più utili che incontrerete è la compressione verticale.
La compressione verticale ci aiuta a ridurre le funzioni verticalmente.
Ma di quanto? Dipende dal fattore di scala.
Prima di iniziare a immergerci più a fondo in questo argomento, assicuriamoci di essere equipaggiati con le giuste tecniche e conoscenze ripassando i seguenti argomenti:
- Comprendere le comuni funzioni padre che potremmo incontrare.
- Rinfrescare la vostra conoscenza delle trasformazioni verticali e orizzontali.
- Imparare come applicare anche gli allungamenti verticali e orizzontali.
In questo articolo, impareremo come identificare le compressioni verticali date due o più espressioni e grafici di funzioni. Applicheremo anche le nostre conoscenze sulle compressioni verticali graficando diversi tipi di funzioni.
Che cos’è una compressione verticale?
Le compressioni verticali si verificano quando una funzione viene moltiplicata per un fattore di scala razionale. La base del grafico della funzione rimane la stessa quando un grafico viene compresso verticalmente. Solo i valori di uscita saranno influenzati.
Perché non osserviamo cosa succede quando f(x) viene compressa verticalmente con un fattore di scala di 1/2 e 1/4?
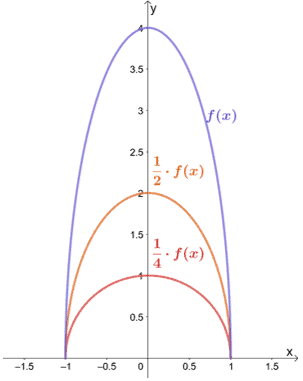
Come ci aspettavamo, quando f(x) viene compressa verticalmente con un fattore di 1/2 e 1/4, anche il grafico viene compresso dello stesso fattore di scala.
In generale, quando una funzione viene compressa verticalmente di a (dove 0 < a < 1), il grafico si restringe dello stesso fattore di scala. Applichiamo il concetto in modo da poter comprimere f(x) = 6|x| + 8 con un fattore di scala di 1/2.
Per comprimere f(x), moltiplichiamo il valore di uscita per 1/2.
1/2 ∙ f(x) = 1/2 (6|x| + 8)
= 3|x| + 4
Ora, cosa succede con le coordinate di una funzione compressa per un fattore di scala di a, dove 0 < a < 1? Se la funzione base passa per il punto (m, n), la funzione compressa verticalmente passerà per il punto (m, an).
Come comprimere verticalmente una funzione? Ora abbiamo capito come la compressione verticale influenza una funzione base. Ora, come applichiamo questa tecnica quando ci viene dato il grafico di una funzione?
Ecco alcuni dei concetti importanti da ricordare quando trasformiamo i grafici e li comprimiamo verticalmente:
- Solo i valori delle coordinate y cambieranno di un fattore di scala di a (controlla se a è una frazione).
- Utilizza i punti critici e alcune coppie ordinate per guidarti nella compressione di un grafico.
- Mantenete l’intercetta/e x del grafico ma anche l’intercetta y diminuirà di un fattore di scala di a.
Perché non proviamo a comprimere y = 4(x- 4) con un fattore di scala di 1/4?
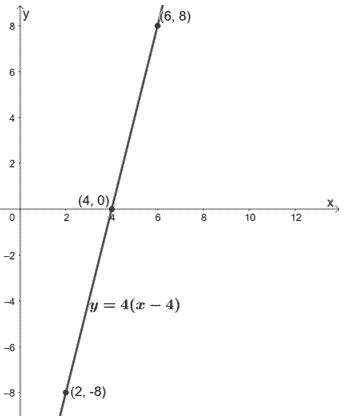
Come abbiamo detto, è importante controllare i punti di riferimento e assicurarsi che possano essere scalati con il giusto fattore. Se vogliamo comprimere y = 4(x- 4) con un fattore di scala di 1/4, avremo i seguenti punti:
- (2, -8) → (2, -2)
- (6, 8) → (6, 2)
- L’intercetta x, (4, 0), rimarrà comunque la stessa.
Una volta che abbiamo alcuni punti per il nuovo grafico compresso, facciamo il grafico della funzione trasformata.
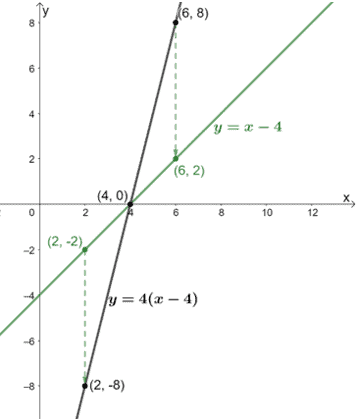
Da questo, possiamo vedere che quando y = 4(x – 4) viene compressa con un fattore di scala di 1/4, la nuova funzione è uguale a y = x – 4.
Possiamo applicare lo stesso processo quando comprimiamo verticalmente altre funzioni. Ma prima, perché non ricapitoliamo quello che abbiamo imparato finora prima di provare altre funzioni e grafici?
Riassunto della definizione di compressione verticale e proprietà
Qui ci sono alcuni importanti promemoria quando si comprime verticalmente il grafico di una data funzione o espressione:
- Quando 0 < a < 1, af(x) restituirà un grafico compresso verticalmente con un fattore di scala di a.
- Applica questo concetto con le coordinate della funzione, così (m, n) diventa (m, an).
- Il valore e la posizione dell’intercetta/e x sono gli stessi.
- Quando f(x) viene compressa verticalmente, il suo dominio rimarrà costante ma il suo intervallo può cambiare.
Siamo ora pronti per provare altri esempi e applicare le nostre nuove conoscenze sulle compressioni verticali. Non dimenticare di rivedere i tuoi appunti!
Esempio 1
La tabella dei valori di f(x) è mostrata qui sotto. Se h(x) = 1/2 ∙ f(x), costruisci una tabella di valori per la funzione h(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 20 | 10 | 4 | 2 | 4 | 10 | 20 |
Soluzione
(1, 2) → (1, 1)
Usa lo stesso ragionamento per completare il resto della tabella dei valori di h(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 10 | 5 | 2 | 1 | 2 | 5 | 10 |
Esempio 2
Usa il grafico mostrato qui sotto per esprimere le relazioni tra i tre.
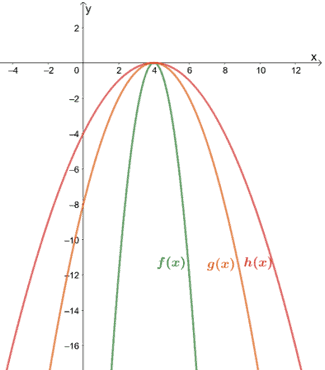
Soluzione
Possiamo andare avanti e controllare alcuni punti di riferimento per osservare le compressioni verticali fatte su ciascuno dei grafici.
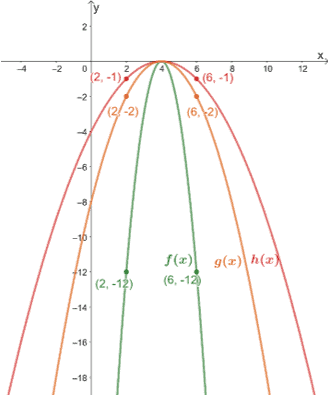
(2, -2) → (2, -12) e (6, -2) → (6, -12)
Dalle due coppie, possiamo vedere che f(x) è il risultato quando g(x) è compresso verticalmente di un fattore di scala 1/6.
(2, -1) → (2, -2) e (6, -1) → (6, -2)
Quindi, h(x) è il risultato quando g(x) è compresso verticalmente di un fattore di scala di 1/2.
c. Osserva le due coppie di punti per trovare il fattore di scala condiviso tra f(x) e h(x).
(2, -1) → (2, -12) e (6, -1) → (6, -12)
Da questo, possiamo vedere che h(x) è il risultato quando f(x) è compresso verticalmente da un fattore di scala di 1/12.
Esempio 3
Traccia la funzione padre di g(x) = 1/4 ∙ √x. Sullo stesso grafico, tracciate g(x) usando le compressioni verticali.
Soluzione
Abbiamo già imparato che la funzione madre delle funzioni di radice quadrata è y = √x. Andiamo avanti e tracciamo prima il grafico di y = √x.
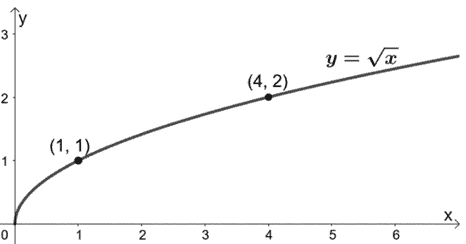
Abbiamo aggiunto alcune coppie ordinate come guide una volta tracciato il grafico di g(x). Poiché vogliamo comprimerla verticalmente, divideremo le coordinate y della funzione madre per 4.
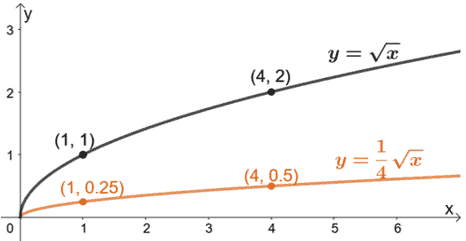
Da qui, abbiamo g(x) rappresentata dal grafico arancione.
Esempio 4
Grafica f(x) = 6 √(9 – x2) trovandone le intercette. Sullo stesso sistema di coordinate, traccia il grafico di g(x) e h(x) date le seguenti condizioni:
- La funzione g(x) è il risultato della compressione verticale di f(x) di un fattore 1/2.
- La funzione h(x) è il risultato della compressione verticale di g(x) di un fattore 1/3.
Soluzione
Come suggerito, andiamo avanti e troviamo le intercette x e y di f(x).
| x | -3 | 0 | 3 |
| f(x) | 0 | 18 | 0 |
Andiamo avanti e tracciamo queste intercette e il grafico di f(x).
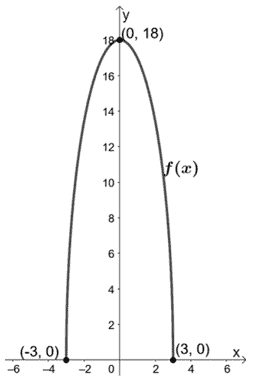
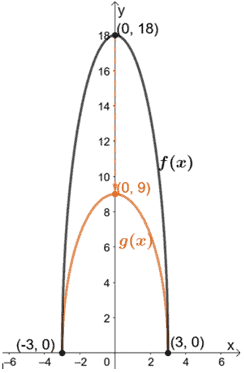
Continuiamo ora a tracciare il grafico di h(x) scalando g(x) verticalmente di 1/3. Questo risulta che h(x) ha un’intercetta y per (0, 3).
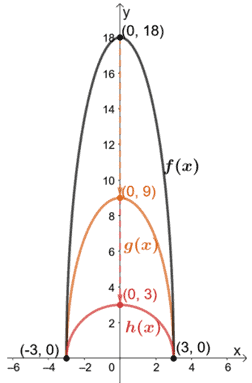
Ora abbiamo le tre funzioni f(x), g(x), e h(x) su un sistema di coordinate. Questo problema conferma anche il fatto che la base del grafico della funzione e le intercette x rimarranno le stesse.
Esempio 5
Descrivi le trasformazioni fatte per ogni coppia di funzioni.
a. g(x) = 3×2 → h(x) = x2/15
b. g(x) = 12x + 4 → h(x) = 3x + 1
c. g(x) = 8|x – 2| – 4 → h(x) = |x -2| – 3
Soluzione
b. Dividendo g(x) per 4 si ottiene (12x + 4)/4 = 3x + 1, quindi h(x) è il risultato della compressione verticale di g(x) con un fattore di scala di 1/4.
Domande pratiche
- La tabella dei valori di f(x) è mostrata sotto. Se h(x) = 1/3∙ f(x), costruisci una tabella di valori per la funzione h(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 30 | 15 | 6 | 3 | 6 | 15 | 30 |
2. Usa il grafico mostrato sotto per esprimere le relazioni tra i tre.
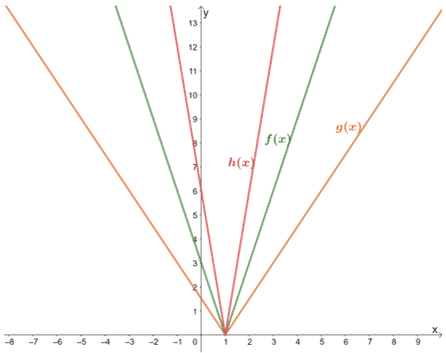
a. Qual è la relazione condivisa tra g(x) e f(x)?
b. Qual è la relazione condivisa tra g(x) e h(x)?
c. Qual è la relazione condivisa tra f(x) e h(x)?
3. Traccia il grafico della funzione padre di g(x) = 1/3 ∙ x2. Sullo stesso grafico, tracciate g(x) usando compressioni verticali.
- La funzione g(x) è il risultato della compressione verticale di f(x) di un fattore 1/4.
- La funzione h(x) è il risultato della compressione verticale di g(x) di un fattore 1/2.
5. Descrivi le trasformazioni fatte per ogni coppia di funzioni.
a. g(x) = 2×2 → h(x) = x2/8
b. g(x) = 36x + 9 → h(x) = 4x + 1
c. g(x) = 6|x + 3| – 6 → h(x) = |x + 3| – 1