Definizione dell’equazione di Schrödinger

L’equazione di Schrödinger, talvolta chiamata equazione d’onda di Schrödinger, è un’equazione differenziale parziale.Utilizza il concetto di conservazione dell’energia (energia cinetica + energia potenziale = energia totale) per ottenere informazioni sul comportamento di un elettrone legato a un nucleo, permettendo di calcolare la funzione d’onda dell’elettrone, Ψ.

La soluzione dell’equazione di Schrödinger ci dà Ψ e Ψ2.Con questi si ottengono i numeri quantici e le forme e gli orientamenti degli orbitali che caratterizzano gli elettroni in un atomo o in una molecola.

L’equazione di Schrödinger dà soluzioni esatte solo per nuclei con un solo elettrone: H, He+, Li2+, Be3+, B4+, C5+, ecc.In linguaggio matematico, si dice che le soluzioni analitiche per Ψ sono possibili solo per sistemi a un elettrone.Per tutti gli altri atomi, ioni e molecole, non sono possibili soluzioni analitiche per Ψ; si utilizzano quindi metodi di calcolo approssimativi, come l’approssimazione orbitale e il teorema di variazione.

C’è un’equazione di Schrödinger dipendente dal tempo e un’equazione di Schrödinger indipendente dal tempo.

L’equazione indipendente dal tempo considera lo stato quantico dell’elettrone immutabile, quindi considera l’elettrone come un’onda fissa.

L’equazione indipendente dal tempo permette di trovare le densità degli elettroni (cioè le dimensioni e le forme degli orbitali atomici e molecolari) usando Ψ2, il quadrato della funzione d’onda.

Gli orbitali p qui sotto sono esempi di Ψ2:

L’equazione diSchrödinger indipendente dal tempo

L’equazione di Schrödinger indipendente dal tempo può essere espressa in stenografia matematica altamente compressa come:

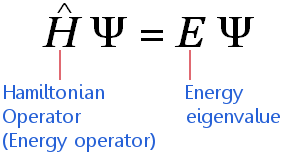
L’equazione si applica agli elettroni che viaggiano a velocità non relativistiche. L’equazione dice:

L’equazione indipendente dal tempo può essere scritta in qualsiasi sistema di coordinate adatto, come le coordinate cartesiane (x,y,z).Per gli atomi idrogenici, le coordinate polari sferiche sono più adatte, quindi:

è la costante di Planck ridotta,

m è la massa dell’elettrone,

è l’operatore Laplaciano,

Ψ è la funzione d’onda,

V è l’energia potenziale,

E è l’autovalore di energia,

(r) indica che le quantità sono funzioni di coordinate polari sferiche (r, θ, φ)

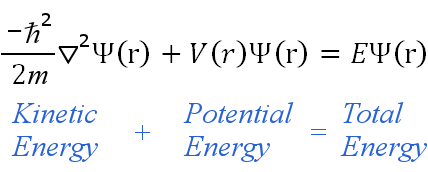
I vincoli portano alla quantizzazione

L’equazione viene risolta per trovare Ψ.I vincoli posti alla risoluzione dell’equazione producono una quantizzazione – cioè le soluzioni trovate per Ψ sono limitate a certi valori e tutti gli altri valori sono proibiti.

Questi vincoli sono:

– Ψ e la sua prima derivata parziale devono essere continui.

– Ψ deve essere normalizzabile: questo significa che c’è il 100% di probabilità che l’elettrone sia da qualche parte nell’universo.Per un Ψ reale valutato, la normalizzazione richiede che:

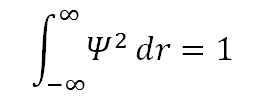
– All’aumentare della distanza dal nucleo, l’elettrone si stacca e non è più legato.cioè all’aumentare di r → ∞, H → H+ + e-.

La funzione d’onda produce numeri quantici

La funzione d’onda dell’elettrone esiste in tre dimensioni, quindi le soluzioni dell’equazione di Schrödinger hanno tre parti, che si ottengono esplicitamente con un metodo di risoluzione delle equazioni differenziali parziali chiamato separazione delle variabili. Facendo questo, otteniamo:

Ψ(r, θ, φ) = R(r) P(θ) F(φ)

Si scopre che le soluzioni per Ψ sono possibili solo quando:

– In R(r), una costante, chiamata n, ha valori 1, 2, 3, 4,….

– In P(θ), una costante, chiamata l, ha valori 0, 1, 2, 3,…(n-1)

– In F(φ), una costante, chiamata ml, ha valori -l, (l+1),…0…, (l+1), l

E così dalla funzione d’onda Ψ l’equazione di Schrödinger ha fornito i tre numeri quantici che caratterizzano il comportamento degli elettroni in un atomo.

– n: il numero quantico principale

– l: il numero quantico del momento angolare orbitale

– ml: il numero quantico magnetico

La funzione d’onda produce forme e dimensioni degli orbitali

Ψ2, la densità di probabilità, definisce le forme e le dimensioni degli orbitali elettronici.