La ricerca sperimentale, spesso considerata il “gold standard” nei disegni di ricerca, è uno dei disegni di ricerca più rigorosi. In questo disegno, una o più variabili indipendenti sono manipolate dal ricercatore (come trattamenti), i soggetti sono assegnati casualmente a diversi livelli di trattamento (assegnazione casuale), e i risultati dei trattamenti sui risultati (variabili dipendenti) sono osservati. La forza unica della ricerca sperimentale è la sua validità interna (causalità) dovuta alla sua capacità di collegare causa ed effetto attraverso la manipolazione del trattamento, mentre si controlla l’effetto spurio della variabile estranea.
La ricerca sperimentale è più adatta alla ricerca esplicativa (piuttosto che alla ricerca descrittiva o esplorativa), dove l’obiettivo dello studio è quello di esaminare le relazioni causa-effetto. Funziona bene anche per la ricerca che coinvolge un insieme relativamente limitato e ben definito di variabili indipendenti che possono essere manipolate o controllate. La ricerca sperimentale può essere condotta in laboratorio o sul campo. Gli esperimenti di laboratorio, condotti in ambienti di laboratorio (artificiali), tendono ad avere un’alta validità interna, ma questo ha il costo di una bassa validità esterna (generalizzabilità), perché l’ambiente artificiale (laboratorio) in cui lo studio è condotto potrebbe non riflettere il mondo reale. Gli esperimenti sul campo, condotti sul campo, come in un’organizzazione reale, e alti in termini di validità interna ed esterna. Ma tali esperimenti sono relativamente rari, a causa delle difficoltà associate alla manipolazione dei trattamenti e al controllo degli effetti estranei in un contesto di campo.
La ricerca sperimentale può essere raggruppata in due grandi categorie: disegni sperimentali veri e propri e disegni quasi-sperimentali. Entrambi i disegni richiedono la manipolazione del trattamento, ma mentre i veri esperimenti richiedono anche l’assegnazione casuale, i quasi-sperimentali no. A volte, ci riferiamo anche alla ricerca non sperimentale, che non è realmente un disegno di ricerca, ma un termine onnicomprensivo che include tutti i tipi di ricerca che non impiegano la manipolazione del trattamento o l’assegnazione casuale, come la ricerca con sondaggio, la ricerca osservazionale e gli studi di correlazione.
Concetti di base
Gruppi di trattamento e di controllo. Nella ricerca sperimentale, ad alcuni soggetti viene somministrato uno o più stimoli sperimentali chiamati trattamento (il gruppo di trattamento) mentre ad altri soggetti non viene dato tale stimolo (il gruppo di controllo). Il trattamento può essere considerato di successo se i soggetti del gruppo di trattamento sono più favorevoli alle variabili di risultato rispetto ai soggetti del gruppo di controllo. Possono essere somministrati più livelli di stimolo sperimentale, nel qual caso, ci può essere più di un gruppo di trattamento. Per esempio, per testare gli effetti di un nuovo farmaco destinato a trattare una certa condizione medica come la demenza, se un campione di pazienti affetti da demenza è diviso a caso in tre gruppi, con il primo gruppo che riceve un alto dosaggio del farmaco, il secondo gruppo che riceve un basso dosaggio, e il terzo gruppo che riceve un placebo come una pillola di zucchero (gruppo di controllo), allora i primi due gruppi sono gruppi sperimentali e il terzo gruppo è un gruppo di controllo. Dopo aver somministrato il farmaco per un periodo di tempo, se le condizioni dei soggetti del gruppo sperimentale sono migliorate significativamente più dei soggetti del gruppo di controllo, possiamo dire che il farmaco è efficace. Possiamo anche confrontare le condizioni dei gruppi sperimentali ad alto e basso dosaggio per determinare se la dose alta è più efficace di quella bassa.
Manipolazione del trattamento. I trattamenti sono la caratteristica unica della ricerca sperimentale che distingue questo disegno da tutti gli altri metodi di ricerca. La manipolazione del trattamento aiuta a controllare la “causa” nelle relazioni causa-effetto. Naturalmente, la validità della ricerca sperimentale dipende da quanto bene è stato manipolato il trattamento. La manipolazione del trattamento deve essere controllata usando pretest e test pilota prima dello studio sperimentale. Tutte le misurazioni condotte prima che il trattamento venga somministrato sono chiamate misure di pretest, mentre quelle condotte dopo il trattamento sono misure di posttest.
Selezione e assegnazione casuale. La selezione casuale è il processo di estrazione casuale di un campione da una popolazione o da una struttura di campionamento. Questo approccio è tipicamente impiegato nella ricerca per sondaggio e assicura che ogni unità della popolazione abbia una possibilità positiva di essere selezionata nel campione. L’assegnazione casuale è invece un processo di assegnazione casuale dei soggetti ai gruppi sperimentali o di controllo. Questa è una pratica standard nella vera ricerca sperimentale per assicurare che i gruppi di trattamento siano simili (equivalenti) tra loro e al gruppo di controllo, prima della somministrazione del trattamento. La selezione casuale è legata al campionamento ed è quindi più strettamente legata alla validità esterna (generalizzabilità) dei risultati. Tuttavia, l’assegnazione casuale è legata al disegno, ed è quindi più legata alla validità interna. È possibile avere sia la selezione che l’assegnazione casuale in una ricerca sperimentale ben progettata, ma la ricerca quasi-sperimentale non comporta né selezione né assegnazione casuale.
Le minacce alla validità interna. Sebbene i disegni sperimentali siano considerati più rigorosi di altri metodi di ricerca in termini di validità interna delle loro inferenze (in virtù della loro capacità di controllare le cause attraverso la manipolazione del trattamento), essi non sono immuni da minacce alla validità interna. Alcune di queste minacce alla validità interna sono descritte di seguito, nel contesto di uno studio sull’impatto di un programma speciale di tutoraggio di matematica per il miglioramento delle abilità matematiche degli studenti delle scuole superiori.
- La minaccia storica è la possibilità che gli effetti osservati (variabili dipendenti) siano causati da eventi estranei o storici piuttosto che dal trattamento sperimentale. Per esempio, il miglioramento del punteggio di matematica post recupero degli studenti potrebbe essere stato causato dalla loro preparazione per un esame di matematica nella loro scuola, piuttosto che dal programma di recupero di matematica.
- La minaccia della maturazione si riferisce alla possibilità che gli effetti osservati siano causati dalla maturazione naturale dei soggetti (ad es, un miglioramento generale nella loro capacità intellettuale di comprendere concetti complessi) piuttosto che dal trattamento sperimentale.
- La minaccia del test è una minaccia nei disegni pre-post in cui le risposte post-test dei soggetti sono condizionate dalle loro risposte pre-test. Per esempio, se gli studenti ricordano le loro risposte dalla valutazione del pretest, possono tendere a ripeterle nell’esame posttest. Non condurre un pretest può aiutare ad evitare questa minaccia.
- La minaccia della strumentazione, che si verifica anche nei progetti pre-post, si riferisce alla possibilità che la differenza tra i punteggi del pretest e del posttest non sia dovuta al programma di recupero della matematica, ma a cambiamenti nel test somministrato, come il posttest che ha un grado di difficoltà maggiore o minore del pretest.
- La minaccia di mortalità si riferisce alla possibilità che i soggetti possano abbandonare lo studio a tassi diversi tra il gruppo di trattamento e quello di controllo a causa di una ragione sistematica, come ad esempio il fatto che gli abbandoni siano per lo più studenti che hanno ottenuto un punteggio basso nel pretest. Se gli studenti a basso rendimento abbandonano, i risultati del posttest saranno artificialmente gonfiati dalla preponderanza di studenti ad alto rendimento.
- La minaccia di regressione, chiamata anche regressione alla media, si riferisce alla tendenza statistica della performance complessiva di un gruppo su una misura durante un posttest a regredire verso la media di quella misura piuttosto che nella direzione prevista. Per esempio, se i soggetti hanno ottenuto un punteggio elevato in un pretest, avranno la tendenza a ottenere un punteggio inferiore nel posttest (più vicino alla media) perché i loro punteggi elevati (lontano dalla media) durante il pretest era probabilmente un’aberrazione statistica. Questo problema tende ad essere più prevalente nei campioni non casuali e quando le due misure sono imperfettamente correlate.
Disegni sperimentali a due gruppi
I disegni sperimentali più semplici sono quelli a due gruppi che coinvolgono un gruppo di trattamento e uno di controllo, e sono ideali per testare gli effetti di una singola variabile indipendente che può essere manipolata come trattamento. I due disegni di base a due gruppi sono il disegno del gruppo di controllo pretest-posttest e il disegno del gruppo di controllo posttest-only, mentre le varianti possono includere disegni di covarianza. Questi disegni sono spesso rappresentati usando una notazione standardizzata del disegno, dove R rappresenta l’assegnazione casuale dei soggetti ai gruppi, X rappresenta il trattamento somministrato al gruppo di trattamento, e O rappresenta le osservazioni pretest o posttest della variabile dipendente (con pedici diversi per distinguere tra le osservazioni pretest e posttest dei gruppi di trattamento e di controllo).
Pretest-posttest control group design . In questo disegno, i soggetti sono assegnati in modo casuale ai gruppi di trattamento e di controllo, sottoposti a una misurazione iniziale (pretest) delle variabili dipendenti di interesse, al gruppo di trattamento viene somministrato un trattamento (che rappresenta la variabile indipendente di interesse), e le variabili dipendenti vengono nuovamente misurate (posttest). La notazione di questo disegno è mostrata nella Figura 10.1.

Figura 10.1. Disegno del gruppo di controllo pretest-posttest
L’effetto E del trattamento sperimentale nel disegno pretest posttest è misurato come la differenza nei punteggi posttest e pretest tra il gruppo di trattamento e quello di controllo:
E = (O 2 – O 1 ) – (O 4 – O 3 )
L’analisi statistica di questo disegno comporta una semplice analisi della varianza (ANOVA) tra il gruppo di trattamento e quello di controllo. Il disegno pretest posttest gestisce diverse minacce alla validità interna, come la maturazione, il test e la regressione, poiché ci si può aspettare che queste minacce influenzino entrambi i gruppi di trattamento e di controllo in modo simile (casuale). La minaccia della selezione è controllata attraverso l’assegnazione casuale. Tuttavia, possono esistere ulteriori minacce alla validità interna. Per esempio, la mortalità può essere un problema se ci sono tassi di abbandono diversi tra i due gruppi, e la misurazione del pretest può influenzare la misurazione del posttest (specialmente se il pretest introduce argomenti o contenuti insoliti).
Posttest-only control group design . Questo disegno è una versione più semplice del disegno pretest-posttest in cui le misurazioni del pretest sono omesse. La notazione del disegno è mostrata nella Figura 10.2.

Figura 10.2. L’effetto del trattamento è misurato semplicemente come la differenza nei punteggi del posttest tra i due gruppi:
E = (O 1 – O 2 )
L’analisi statistica appropriata di questo disegno è anche un’analisi della varianza a due gruppi (ANOVA). La semplicità di questo disegno lo rende più attraente del disegno pretest-posttest in termini di validità interna. Questo disegno controlla la maturazione, il test, la regressione, la selezione e l’interazione pretest-posttest, anche se la minaccia di mortalità può continuare ad esistere.
Disegni di covarianza. A volte, le misure delle variabili dipendenti possono essere influenzate da variabili estranee chiamate covariate. Le covariate sono quelle variabili che non sono di interesse centrale per uno studio sperimentale, ma dovrebbero comunque essere controllate in un disegno sperimentale al fine di eliminare il loro potenziale effetto sulla variabile dipendente e quindi consentire una rilevazione più accurata degli effetti delle variabili indipendenti di interesse. I disegni sperimentali discussi in precedenza non controllavano tali covarianti. Un disegno di covarianza (chiamato anche disegno di variabile concomitante) è un tipo speciale di disegno di gruppo di controllo pretest posttest dove la misura pretest è essenzialmente una misura delle covariate di interesse piuttosto che quella delle variabili dipendenti. La notazione del disegno è mostrata nella Figura 10.3, dove C rappresenta le covariate:

Figura 10.3. Disegno di covarianza
Perché la misura del pretest non è una misura della variabile dipendente, ma piuttosto una covariata, l’effetto del trattamento è misurato come la differenza nei punteggi del posttest tra il gruppo di trattamento e quello di controllo come:
E = (O 1 – O 2 )
A causa della presenza di covariate, la giusta analisi statistica di questo disegno è un’analisi di covarianza a due gruppi (ANCOVA). Questo disegno ha tutti i vantaggi del disegno di solo post-test, ma con una validità interna dovuta al controllo delle covarianti. I disegni di covarianza possono anche essere estesi al disegno di gruppo di controllo pretest-posttest. 
Disegni fattoriali
I disegni a due gruppi sono inadeguati se la vostra ricerca richiede la manipolazione di due o più variabili indipendenti (trattamenti). In questi casi, avrete bisogno di disegni a quattro o più gruppi. Tali disegni, abbastanza popolari nella ricerca sperimentale, sono comunemente chiamati disegni fattoriali. Ogni variabile indipendente in questo disegno è chiamata fattore, e ogni suddivisione di un fattore è chiamata livello. I disegni fattoriali permettono al ricercatore di esaminare non solo l’effetto individuale di ogni trattamento sulle variabili dipendenti (chiamati effetti principali), ma anche il loro effetto congiunto (chiamati effetti di interazione).
Il disegno fattoriale più basilare è un disegno fattoriale 2 x 2, che consiste in due trattamenti, ciascuno con due livelli (come alto/basso o presente/assente). Per esempio, diciamo che vuoi confrontare i risultati di apprendimento di due diversi tipi di tecniche di istruzione (istruzione in classe e online), e vuoi anche esaminare se questi effetti variano con il tempo di istruzione (1,5 o 3 ore a settimana). In questo caso, avete due fattori: tipo di istruzione e tempo di istruzione; ciascuno con due livelli (in classe e online per il tipo di istruzione, e 1,5 e 3 ore/settimana per il tempo di istruzione), come mostrato nella Figura 8.1. Se si desidera aggiungere un terzo livello di tempo di istruzione (diciamo 6 ore/settimana), allora il secondo fattore sarà composto da tre livelli e si avrà un disegno fattoriale 2 x 3. D’altra parte, se si desidera aggiungere un terzo fattore come il lavoro di gruppo (presente contro assente), si avrà un disegno fattoriale 2 x 2 x 2. In questa notazione, ogni numero rappresenta un fattore, e il valore di ogni fattore rappresenta il numero di livelli in quel fattore.

Figura 10.4. Disegno fattoriale 2 x 2
I disegni fattoriali possono anche essere rappresentati usando una notazione di disegno, come quella mostrata nel pannello di destra della Figura 10.4. R rappresenta l’assegnazione casuale dei soggetti ai gruppi di trattamento, X rappresenta i gruppi di trattamento stessi (i pedici di X rappresentano il livello di ogni fattore), e O rappresentano le osservazioni della variabile dipendente. Si noti che il disegno fattoriale 2 x 2 avrà quattro gruppi di trattamento, corrispondenti alle quattro combinazioni dei due livelli di ciascun fattore. Corrispondentemente, il disegno 2 x 3 avrà sei gruppi di trattamento, e il disegno 2 x 2 x 2 avrà otto gruppi di trattamento. Come regola generale, ogni cella in un disegno fattoriale dovrebbe avere una dimensione minima del campione di 20 (questa stima è derivata dai calcoli della potenza di Cohen basati su dimensioni medie dell’effetto). Quindi un disegno fattoriale 2 x 2 x 2 richiede una dimensione minima totale del campione di 160 soggetti, con almeno 20 soggetti in ogni cella. Come potete vedere, il costo della raccolta dei dati può aumentare sostanzialmente con più livelli o fattori nel vostro disegno fattoriale. A volte, a causa di limiti di risorse, alcune celle in tali disegni fattoriali possono non ricevere alcun trattamento, che sono chiamati disegni fattoriali incompleti. Tali disegni incompleti danneggiano la nostra capacità di trarre inferenze sui fattori incompleti.
In un disegno fattoriale, si dice che esiste un effetto principale se la variabile dipendente mostra una differenza significativa tra più livelli di un fattore, a tutti i livelli di altri fattori. Nessun cambiamento nella variabile dipendente attraverso i livelli dei fattori è il caso nullo (linea di base), da cui si valutano gli effetti principali. Nell’esempio precedente, si può vedere un effetto principale del tipo di istruzione, del tempo di istruzione o di entrambi sui risultati di apprendimento. Un effetto di interazione esiste quando l’effetto delle differenze in un fattore dipende dal livello di un secondo fattore. Nel nostro esempio, se l’effetto del tipo di istruzione sui risultati di apprendimento è maggiore per 3 ore/settimana di tempo di istruzione che per 1,5 ore/settimana, allora possiamo dire che c’è un effetto di interazione tra tipo di istruzione e tempo di istruzione sui risultati di apprendimento. Si noti che la presenza di effetti di interazione domina e rende irrilevanti gli effetti principali, e non è significativo interpretare gli effetti principali se gli effetti di interazione sono significativi.
Disegni sperimentali ibridi
I disegni ibridi sono quelli che sono formati dalla combinazione di caratteristiche di disegni più consolidati. Tre di questi disegni ibridi sono il disegno a blocchi randomizzati, il disegno a quattro gruppi di Salomone e il disegno a repliche commutate.
Disegno a blocchi randomizzati. Si tratta di una variazione del disegno di gruppo di controllo post-test-only o pretest-post-test in cui la popolazione dei soggetti può essere raggruppata in sottogruppi relativamente omogenei (chiamati blocchi) all’interno dei quali l’esperimento viene replicato. Per esempio, se si vuole replicare lo stesso disegno post-test-only tra studenti universitari e professionisti che lavorano a tempo pieno (due blocchi omogenei), i soggetti in entrambi i blocchi sono divisi a caso tra gruppo di trattamento (che riceve lo stesso trattamento) o gruppo di controllo (vedi Figura 10.5). Lo scopo di questo disegno è quello di ridurre il “rumore” o la varianza nei dati che può essere attribuibile alle differenze tra i blocchi in modo che l’effetto reale di interesse possa essere rilevato più accuratamente.
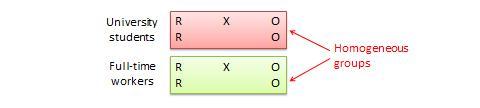
Figura 10.5. Disegno a blocchi randomizzati.
Disegno a quattro gruppi di Salomone. In questo disegno, il campione è diviso in due gruppi di trattamento e due gruppi di controllo. Un gruppo di trattamento e un gruppo di controllo ricevono il pretest e gli altri due gruppi no. Questo disegno rappresenta una combinazione di disegno di gruppo di controllo pretest-only e pretest-posttest, ed è destinato a testare il potenziale effetto di distorsione della misurazione del pretest sulle misure posttest che tende a verificarsi nei disegni pretest-posttest ma non nei disegni posttest only. La notazione del disegno è mostrata nella Figura 10.6.

Figura 10.6. Disegno a quattro gruppi di Salomone
Disegno a replicazione commutata. Questo è un disegno a due gruppi implementato in due fasi con tre ondate di misurazione. Il gruppo di trattamento nella prima fase serve come gruppo di controllo nella seconda fase, e il gruppo di controllo nella prima fase diventa il gruppo di trattamento nella seconda fase, come illustrato nella Figura 10.7. In altre parole, il disegno originale viene ripetuto o replicato temporalmente con i ruoli di trattamento/controllo scambiati tra i due gruppi. Alla fine dello studio, tutti i partecipanti avranno ricevuto il trattamento durante la prima o la seconda fase. Questo disegno è più fattibile in contesti organizzativi in cui i programmi organizzativi (ad esempio, la formazione dei dipendenti) sono implementati in modo graduale o sono ripetuti a intervalli regolari.
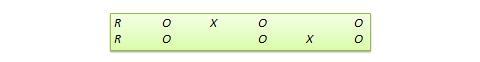
Figura 10.7. Disegno di replica commutata.
Disegni quasi sperimentali
I disegni quasi sperimentali sono quasi identici ai veri disegni sperimentali, ma mancano di un ingrediente chiave: l’assegnazione casuale. Per esempio, un’intera sezione della classe o un’organizzazione è usata come gruppo di trattamento, mentre un’altra sezione della stessa classe o un’organizzazione diversa nello stesso settore è usata come gruppo di controllo. Questa mancanza di assegnazione casuale si traduce potenzialmente in gruppi che non sono equivalenti, come ad esempio un gruppo che possiede una maggiore padronanza di un certo contenuto rispetto all’altro gruppo, ad esempio in virtù del fatto che ha avuto un insegnante migliore in un semestre precedente, il che introduce la possibilità di bias di selezione. I disegni quasi-sperimentali sono quindi inferiori ai veri disegni sperimentali nella validità dell’intervallo a causa della presenza di una varietà di minacce legate alla selezione, come la minaccia di selezione-maturazione (i gruppi di trattamento e di controllo maturano a ritmi diversi), la minaccia di selezione-storia (i gruppi di trattamento e di controllo hanno un impatto diverso da eventi estranei o storici), minaccia di regressione della selezione (i gruppi di trattamento e di controllo che regrediscono verso la media tra il pretest e il posttest a tassi diversi), minaccia di selezione-strumentazione (i gruppi di trattamento e di controllo che rispondono in modo diverso alla misurazione), selezione-test (i gruppi di trattamento e di controllo che rispondono in modo diverso al pretest), e selezione-mortalità (i gruppi di trattamento e di controllo che mostrano tassi di abbandono diversi). Date queste minacce alla selezione, è generalmente preferibile evitare i disegni quasi-sperimentali il più possibile.
Molti veri disegni sperimentali possono essere convertiti in disegni quasi-sperimentali omettendo l’assegnazione casuale. Per esempio, la versione quasi-equivalente del disegno di gruppo di controllo pretest-posttest è chiamata disegno a gruppi non equivalenti (NEGD), come mostrato nella Figura 10.8, con l’assegnazione casuale R sostituita dall’assegnazione non equivalente (non casuale) N . Allo stesso modo, la versione quasi sperimentale del disegno di replicazione commutata è chiamata disegno di replicazione commutata non equivalente (vedi Figura 10.9).

Figura 10.8. Disegno NEGD.
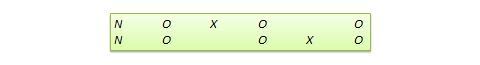
Figura 10.9. Disegno di replicazione commutato non equivalente.
Inoltre, ci sono un bel po’ di disegni non equivalenti unici senza corrispondenti cugini veri disegni sperimentali. Alcuni dei più utili di questi disegni sono discussi di seguito.
Disegno di discontinuità di regressione (RD). Questo è un disegno pretest-posttest non equivalente in cui i soggetti sono assegnati al trattamento o al gruppo di controllo in base a un punteggio di cutoff su una misura pre-programma. Per esempio, i pazienti che sono gravemente malati possono essere assegnati a un gruppo di trattamento per testare l’efficacia di un nuovo farmaco o protocollo di trattamento e quelli che sono leggermente malati sono assegnati al gruppo di controllo. In un altro esempio, gli studenti che sono in ritardo nei punteggi dei test standardizzati possono essere selezionati per un programma di recupero destinato a migliorare le loro prestazioni, mentre quelli che ottengono un punteggio elevato in tali test non vengono selezionati dal programma di recupero. La notazione del progetto può essere rappresentata come segue, dove C rappresenta il punteggio di cutoff:
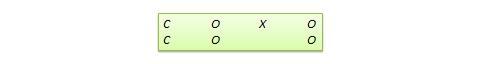
Figura 10.10. Disegno RD.
A causa dell’uso di un punteggio di cutoff, è possibile che i risultati osservati siano una funzione del punteggio di cutoff piuttosto che del trattamento, il che introduce una nuova minaccia alla validità interna. Tuttavia, l’uso del punteggio di cutoff assicura anche che le risorse limitate o costose siano distribuite alle persone che ne hanno più bisogno piuttosto che in modo casuale in una popolazione, permettendo contemporaneamente un trattamento quasi sperimentale. I punteggi del gruppo di controllo nel disegno RD non servono come punto di riferimento per confrontare i punteggi del gruppo di trattamento, data la non equivalenza sistematica tra i due gruppi. Piuttosto, se non c’è discontinuità tra i punteggi pretest e posttest nel gruppo di controllo, ma tale discontinuità persiste nel gruppo di trattamento, allora questa discontinuità è vista come prova dell’effetto del trattamento. Questo disegno, mostrato nella Figura 10.11, è molto simile al disegno standard NEGD (pretest-posttest), con una differenza fondamentale: il punteggio del pretest viene raccolto dopo la somministrazione del trattamento. Un’applicazione tipica di questo disegno è quando un ricercatore viene coinvolto per testare l’efficacia di un programma (ad esempio, un programma educativo) dopo che il programma è già iniziato e i dati del pretest non sono disponibili. In tali circostanze, l’opzione migliore per il ricercatore è spesso quella di utilizzare un’altra misura preregistrata, come la media dei voti degli studenti prima dell’inizio del programma, come proxy per i dati del pretest. Una variante del progetto del proxy pretest consiste nell’utilizzare il ricordo post-test dei dati del pretest da parte dei soggetti, che può essere soggetto a distorsioni nel ricordo, ma può comunque fornire una misura del guadagno percepito o del cambiamento nella variabile dipendente.
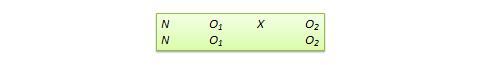
Figura 10.11. Disegno di pretest proxy.
Disegno di campioni separati pretest-posttest. Questo disegno è utile se non è possibile raccogliere dati pretest e posttest dagli stessi soggetti per qualche motivo. Come mostrato nella Figura 10.12, ci sono quattro gruppi in questo disegno, ma due gruppi provengono da un singolo gruppo non equivalente, mentre gli altri due gruppi provengono da un diverso gruppo non equivalente. Per esempio, si vuole testare la soddisfazione dei clienti con un nuovo servizio online che viene implementato in una città ma non in un’altra. In questo caso, i clienti della prima città servono come gruppo di trattamento e quelli della seconda città costituiscono il gruppo di controllo. Se non è possibile ottenere misure pretest e posttest dagli stessi clienti, è possibile misurare la soddisfazione del cliente in un momento, implementare il nuovo programma di servizi e misurare la soddisfazione del cliente (con un diverso gruppo di clienti) dopo l’implementazione del programma. La soddisfazione dei clienti viene misurata anche nel gruppo di controllo negli stessi momenti del gruppo di trattamento, ma senza l’implementazione del nuovo programma. Il disegno non è particolarmente forte, perché non si possono esaminare i cambiamenti nel punteggio di soddisfazione di ogni specifico cliente prima e dopo l’implementazione, ma si possono solo esaminare i punteggi medi di soddisfazione dei clienti. Nonostante la minore validità interna, questo disegno può ancora essere un modo utile per raccogliere dati quasi sperimentali quando i dati pretest e posttest non sono disponibili dagli stessi soggetti.

Figura 10.12. Disegno di campioni separati pretest-posttest.
Disegno di variabile dipendente non equivalente (NEDV). Si tratta di un disegno quasi sperimentale pre-post a gruppo unico con due misure di risultato, dove ci si aspetta che una misura sia teoricamente influenzata dal trattamento e l’altra no. Per esempio, se si sta progettando un nuovo curriculum di calcolo per gli studenti delle scuole superiori, è probabile che questo curriculum influenzi i punteggi di calcolo post-test degli studenti ma non quelli di algebra. Tuttavia, i punteggi post-test di algebra possono ancora variare a causa di fattori estranei come la storia o la maturazione. Quindi, i punteggi pre-post di algebra possono essere usati come misura di controllo, mentre quelli del calcolo pre-post possono essere trattati come misura di trattamento. La notazione del disegno, mostrata nella Figura 10.13, indica il singolo gruppo con un singolo N, seguito dal pretest O 1 e dal posttest O 2 per calcolo e algebra per lo stesso gruppo di studenti. Questo disegno è debole in termini di validità interna, ma il suo vantaggio sta nel non dover utilizzare un gruppo di controllo separato.
Un’interessante variazione del disegno NEDV è un disegno NEDV corrispondente al modello, che impiega più variabili di risultato e una teoria che spiega quanto ogni variabile sarà influenzata dal trattamento. Il ricercatore può quindi esaminare se la previsione teorica trova corrispondenza nelle osservazioni reali. Questa tecnica di pattern-matching, basata sul grado di corrispondenza tra i modelli teorici e quelli osservati, è un modo potente di alleviare i problemi di validità interna del disegno originale NEDV.
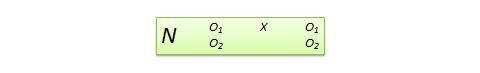
Figura 10.13. Disegno NEDV.
Pericoli della ricerca sperimentale
La ricerca sperimentale è uno dei disegni di ricerca più difficili e non dovrebbe essere presa alla leggera. Questo tipo di ricerca è spesso il migliore con una moltitudine di problemi metodologici. In primo luogo, anche se la ricerca sperimentale richiede teorie per inquadrare le ipotesi da testare, gran parte della ricerca sperimentale attuale è ateoretica. Senza teorie, le ipotesi testate tendono ad essere ad hoc, possibilmente illogiche e senza senso. In secondo luogo, molti degli strumenti di misurazione usati nella ricerca sperimentale non sono testati per l’affidabilità e la validità, e sono incomparabili tra gli studi. Di conseguenza, anche i risultati generati utilizzando tali strumenti sono incomparabili. In terzo luogo, molte ricerche sperimentali usano disegni di ricerca inappropriati, come variabili dipendenti irrilevanti, nessun effetto di interazione, nessun controllo sperimentale, e stimoli non equivalenti tra i gruppi di trattamento. I risultati di tali studi tendono a mancare di validità interna e sono altamente sospetti. Quarto, i trattamenti (compiti) usati nella ricerca sperimentale possono essere diversi, incomparabili e incoerenti tra gli studi e talvolta inappropriati per la popolazione dei soggetti. Per esempio, ai soggetti studenti universitari viene spesso chiesto di fingere di essere manager di marketing e di eseguire un complesso compito di allocazione del budget in cui non hanno alcuna esperienza o competenza. L’uso di questi compiti inappropriati introduce nuove minacce alla validità interna (cioè, la performance del soggetto può essere un artefatto del contenuto o della difficoltà dell’impostazione del compito), genera risultati che non sono interpretabili e privi di significato, e rende impossibile l’integrazione dei risultati tra gli studi.
Il disegno di trattamenti sperimentali adeguati è un compito molto importante nel disegno sperimentale, perché il trattamento è la raison d’etre del metodo sperimentale, e non deve mai essere affrettato o trascurato. Per progettare un compito adeguato e appropriato, i ricercatori dovrebbero utilizzare compiti prevalidati, se disponibili, condurre controlli sulla manipolazione del trattamento per verificare l’adeguatezza di tali compiti (interrogando i soggetti dopo aver eseguito il compito assegnato), condurre test pilota (ripetutamente, se necessario) e, in caso di dubbio, utilizzare compiti più semplici e familiari per il campione intervistato rispetto a quelli complessi o poco familiari.
In sintesi, questo capitolo ha introdotto concetti chiave nel metodo di ricerca del disegno sperimentale e ha introdotto una varietà di veri disegni sperimentali e quasi sperimentali. Anche se questi disegni variano ampiamente in termini di validità interna, i disegni con minore validità interna non dovrebbero essere trascurati e a volte possono essere utili in circostanze specifiche e contingenze empiriche.