Sviluppo della distribuzione di Boltzmann
I metodi statistici diventano un modo più preciso per studiare la natura quando il numero di particelle è grande. Così ci aspettiamo che la descrizione delle velocità delle molecole in un gas sia di fatto la distribuzione più probabile, dato che abbiamo a che fare con numeri di particelle nell’intervallo del numero di Avogadro. Ma questa distribuzione più probabile (la distribuzione di Maxwell-Boltzmann) è soggetta a vincoli, cioè che il numero di particelle è costante e che l’energia totale è costante (conservazione dell’energia). Massimizzare la distribuzione di probabilità soggetta a questi vincoli in generale è un compito matematico formidabile (vedi Richtmyer, et al., per esempio). Un modo per avvicinarsi alla soluzione in modo più intuitivo è quello di trattare un esempio fisico che conosciamo – vale a dire la fisica di un’atmosfera sotto l’influenza della gravità come si riflette nella formula barometrica. La seguente trattazione segue lo sviluppo di Rohlf.
In questo approccio facciamo uso del fatto che l’energia cinetica media delle molecole può essere espressa in termini di temperatura cinetica. Inoltre, sappiamo che la conservazione dell’energia in questo caso comporta solo il bilanciamento dell’energia cinetica e dell’energia potenziale gravitazionale, finché trattiamo l’atmosfera come un gas ideale.
Dall’espressione della temperatura cinetica
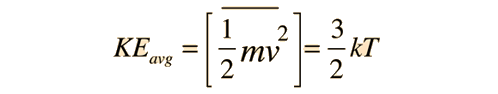
abbiamo un’espressione sperimentalmente testata per l’energia cinetica molecolare. Nella formula barometrica:
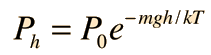
abbiamo una descrizione di un sistema di gas ideale che può essere usata per aiutare a sviluppare un argomento di plausibilità per la distribuzione della velocità di Maxwell. I passi di questo processo sono i seguenti:
Relare la velocità delle particelle all’altezza.
Relare il flusso delle particelle alla distribuzione della velocità.
Relare la distribuzione della velocità alla formula barometrica.
Calcolare la distribuzione della velocità e normalizzarla.
Per una direzione nello spazio questo processo produce l’espressione:

e quando tutte le direzioni di velocità sono incluse, diventa la relazione di distribuzione della velocità di Maxwell:
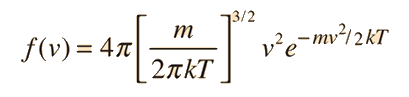 |
Perché questa relazione è sbilanciata verso velocità maggiori mentre quella direttamente sopra non lo è? |
Bisogna notare che sebbene abbiamo usato una situazione fisica dipendente dalla gravità per ottenere la distribuzione delle velocità, la gravità non appare nel risultato finale. Cioè, il risultato ottenuto è generale e non contiene g. La formula barometrica è stata semplicemente usata come un costrutto per mettere in relazione la distribuzione di velocità con i vincoli di energia e numero di particelle.