Un test t è un test statistico che viene utilizzato per confrontare le medie di due gruppi. È spesso usato nei test di ipotesi per determinare se un processo o un trattamento ha effettivamente un effetto sulla popolazione di interesse, o se due gruppi sono diversi l’uno dall’altro.
Vuoi sapere se la lunghezza media dei petali dei fiori di iris differisce a seconda della loro specie. Trovate due specie diverse di iris che crescono in un giardino e misurate 25 petali di ogni specie. Potete testare la differenza tra questi due gruppi usando un test t.
- L’ipotesi nulla (H0) è che la vera differenza tra queste medie di gruppo sia zero.
- L’ipotesi alternativa (Ha) è che la vera differenza sia diversa da zero.
Quando usare un test t
Un test t può essere usato solo quando si confrontano le medie di due gruppi (un confronto a coppie). Se vuoi confrontare più di due gruppi, o se vuoi fare più confronti a coppie, usa un test ANOVA o un test post-hoc.
Il t-test è un test parametrico di differenza, il che significa che fa le stesse assunzioni sui tuoi dati degli altri test parametrici. Il test t assume che i tuoi dati:
- sono indipendenti
- sono (approssimativamente) distribuiti normalmente.
- hanno una quantità simile di varianza all’interno di ogni gruppo confrontato (cioè omogeneità della varianza)
Se i tuoi dati non soddisfano queste ipotesi, puoi provare un’alternativa non parametrica al test t, come il test Wilcoxon Signed-Rank per dati con varianze disuguali.
Quale tipo di t-test dovrei usare?
Quando scegliete un t-test, dovrete considerare due cose: se i gruppi da confrontare provengono da una sola popolazione o da due popolazioni diverse, e se volete testare la differenza in una direzione specifica.
Test a un campione, a due campioni o a coppie?
- Se i gruppi provengono da una singola popolazione (ad esempio misurando prima e dopo un trattamento sperimentale), esegui un t-test a coppie.
- Se i gruppi provengono da due popolazioni diverse (ad esempio due specie diverse, o persone di due città diverse), esegui un t-test a due campioni (noto anche come t-test indipendente).
- Se c’è un gruppo da confrontare contro un valore standard (ad es.Ad esempio, confrontando l’acidità di un liquido con un pH neutro di 7, si esegue un t-test a un campione.
Test a una o due code?
- Se vi interessa solo sapere se le due popolazioni sono diverse tra loro, eseguite un t-test a due code.
- Se volete sapere se la media di una popolazione è maggiore o minore dell’altra, eseguite un t-test a una coda.
Nel tuo test per stabilire se la lunghezza dei petali differisce in base alla specie:
- Le tue osservazioni provengono da due popolazioni separate (specie separate), quindi esegui un t-test a due campioni.
- Non ti interessa la direzione della differenza, ma solo se c’è una differenza, quindi scegli di usare un t-test a due code.
Eseguire un t-test
Il test t stima la vera differenza tra due medie di gruppo usando il rapporto tra la differenza tra le medie di gruppo e l’errore standard di entrambi i gruppi. Puoi calcolarlo manualmente usando una formula, o usare un software di analisi statistica.
Formula del test t
La formula per il test t a due campioni (noto anche come test t di Student) è mostrata qui sotto.
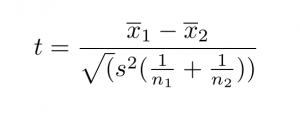
In questa formula, t è il valore t, x1 e x2 sono le medie dei due gruppi da confrontare, s2 è l’errore standard dei due gruppi, e n1 e n2 sono il numero di osservazioni in ciascuno dei gruppi.
Un valore t più grande mostra che la differenza tra le medie del gruppo è maggiore dell’errore standard raggruppato, indicando una differenza più significativa tra i gruppi.
Puoi confrontare il tuo valore t calcolato con i valori in un grafico dei valori critici per determinare se il tuo valore t è maggiore di quello che ci si aspetterebbe dal caso. Se è così, puoi rifiutare l’ipotesi nulla e concludere che i due gruppi sono effettivamente diversi.
Funzione t-test nel software statistico
La maggior parte dei software statistici (R, SPSS, ecc.) include una funzione t-test. Questa funzione incorporata prenderà i vostri dati grezzi e calcolerà il valore t. Poi lo confronta con il valore critico e calcola un valore p. In questo modo potete vedere rapidamente se i vostri gruppi sono statisticamente diversi.
Nel vostro confronto delle lunghezze dei petali dei fiori, decidete di eseguire il vostro t-test usando R. Il codice assomiglia a questo:
Scaricate il set di dati per fare pratica da soli.
Serie di dati campione
Interpretare i risultati del test
Se si esegue il test t per l’ipotesi del fiore in R, si riceverà il seguente output:


L’output fornisce:
- una spiegazione di ciò che viene confrontato, chiamato dati nella tabella di output.
- Il valore t: -33,719. Notate che è negativo; questo va bene! Nella maggior parte dei casi, ci interessa solo il valore assoluto della differenza, o la distanza da 0. Non importa quale direzione.
- I gradi di libertà: 30.196. I gradi di libertà sono legati alla dimensione del campione e mostrano quanti punti dati ‘liberi’ sono disponibili nel test per fare confronti. Maggiori sono i gradi di libertà, meglio funzionerà il vostro test statistico.
- Il p-value: 2.2e-16 (cioè 2.2 con 15 zeri davanti). Questo descrive la probabilità di vedere un valore t grande come questo per caso.
- Una dichiarazione dell’ipotesi alternativa (Ha). In questo test, l’Ha è che la differenza non è 0.
- L’intervallo di confidenza del 95%. Questo è l’intervallo di numeri all’interno del quale la vera differenza nei mezzi sarà il 95% delle volte. Questo può essere cambiato dal 95% se volete un intervallo più grande o più piccolo, ma il 95% è molto comunemente usato.
- La lunghezza media dei petali per ogni gruppo.
Presentare i risultati di un test t
Quando si riportano i risultati del test t, i valori più importanti da includere sono il valore t, il valore p e i gradi di libertà del test. Questi comunicheranno al vostro pubblico se la differenza tra i due gruppi è statisticamente significativa (vale a dire che è improbabile che sia avvenuta per caso).
Potete anche includere le statistiche riassuntive per i gruppi confrontati, cioè la media e la deviazione standard. In R, il codice per calcolare la media e la deviazione standard dai dati si presenta così:
flower.data %>%
group_by(Species) %>%
summarize(mean_length = mean(Petal.Length),
sd_length = sd(Petal.Length))
Nel nostro esempio, riporteresti i risultati in questo modo:
Domande frequenti sui test t
Un t-test è un test statistico che confronta le medie di due campioni. Viene utilizzato nei test d’ipotesi, con un’ipotesi nulla che la differenza nelle medie di gruppo sia zero e un’ipotesi alternativa che la differenza nelle medie di gruppo sia diversa da zero.
Un t-test misura la differenza tra le medie di gruppo divisa per l’errore standard aggregato delle due medie di gruppo.
In questo modo, calcola un numero (il valore t) che illustra l’ampiezza della differenza tra le due medie di gruppo confrontate, e stima la probabilità che questa differenza esista solo per caso (valore p).
La tua scelta del t-test dipende dal fatto che tu stia studiando un gruppo o due gruppi, e se ti interessa la direzione della differenza nelle medie di gruppo.
Se stai studiando un gruppo, usa un t-test a coppie per confrontare la media del gruppo nel tempo o dopo un intervento, o usa un t-test a un campione per confrontare la media del gruppo con un valore standard. Se state studiando due gruppi, usate un t-test a due campioni.
Se volete sapere solo se esiste una differenza, usate un test a due code. Se vuoi sapere se la media di un gruppo è maggiore o minore dell’altra, usa un test a una coda a sinistra o a destra.
Un t-test a un campione è usato per confrontare una singola popolazione con un valore standard (per esempio, per determinare se la durata media della vita di una specifica città è diversa dalla media del paese).
Un t-test appaiato è usato per confrontare una singola popolazione prima e dopo un intervento sperimentale o in due momenti diversi (per esempio, misurando le prestazioni degli studenti in un test prima e dopo l’insegnamento del materiale).
Un t-test non dovrebbe essere usato per misurare le differenze tra più di due gruppi, perché la struttura dell’errore di un t-test sottostima l’errore reale quando si confrontano molti gruppi.
Se vuoi confrontare le medie di più gruppi contemporaneamente, è meglio usare un altro test statistico come l’ANOVA o un test post-hoc.
