La investigación experimental, a menudo considerada como el «estándar de oro» en los diseños de investigación, es uno de los más rigurosos de todos los diseños de investigación. En este diseño, el investigador manipula una o más variables independientes (como tratamientos), los sujetos son asignados aleatoriamente a diferentes niveles de tratamiento (asignación aleatoria) y se observan los resultados de los tratamientos sobre los resultados (variables dependientes). La fuerza única de la investigación experimental es su validez interna (causalidad) debido a su capacidad para vincular la causa y el efecto a través de la manipulación del tratamiento, al tiempo que se controla el efecto espurio de las variables extrañas.
La investigación experimental es más adecuada para la investigación explicativa (que para la investigación descriptiva o exploratoria), donde el objetivo del estudio es examinar las relaciones causa-efecto. También funciona bien para la investigación que implica un conjunto relativamente limitado y bien definido de variables independientes que pueden ser manipuladas o controladas. La investigación experimental puede llevarse a cabo en entornos de laboratorio o de campo. Los experimentos de laboratorio, realizados en entornos de laboratorio (artificiales), tienden a tener una alta validez interna, pero a costa de una baja validez externa (generalizabilidad), porque el entorno artificial (de laboratorio) en el que se realiza el estudio puede no reflejar el mundo real. Los experimentos de campo, realizados en entornos de campo como en una organización real, tienen una alta validez interna y externa. Pero tales experimentos son relativamente raros, debido a las dificultades asociadas con la manipulación de los tratamientos y el control de los efectos extraños en un entorno de campo.
La investigación experimental puede agruparse en dos grandes categorías: diseños experimentales verdaderos y diseños cuasi-experimentales. Ambos diseños requieren la manipulación del tratamiento, pero mientras que los experimentos verdaderos también requieren la asignación aleatoria, los cuasi-experimentos no. A veces, también nos referimos a la investigación no experimental, que no es realmente un diseño de investigación, sino un término que incluye todos los tipos de investigación que no emplean la manipulación del tratamiento o la asignación aleatoria, como la investigación por encuesta, la investigación observacional y los estudios correlacionales.
Conceptos básicos
Grupos de tratamiento y de control. En la investigación experimental, a algunos sujetos se les administra uno o más estímulos experimentales denominados tratamiento (el grupo de tratamiento ) mientras que a otros sujetos no se les administra dicho estímulo (el grupo de control ). El tratamiento puede considerarse exitoso si los sujetos del grupo de tratamiento obtienen una puntuación más favorable en las variables de resultado que los sujetos del grupo de control. Pueden administrarse múltiples niveles de estímulo experimental, en cuyo caso puede haber más de un grupo de tratamiento. Por ejemplo, para probar los efectos de un nuevo fármaco destinado a tratar una determinada afección médica como la demencia, si una muestra de pacientes con demencia se divide aleatoriamente en tres grupos, en los que el primer grupo recibe una dosis alta del fármaco, el segundo grupo recibe una dosis baja y el tercer grupo recibe un placebo como una píldora de azúcar (grupo de control), entonces los dos primeros grupos son grupos experimentales y el tercer grupo es un grupo de control. Tras administrar el fármaco durante un periodo de tiempo, si el estado de los sujetos del grupo experimental mejora significativamente más que el de los sujetos del grupo de control, podemos decir que el fármaco es eficaz. También podemos comparar las condiciones de los grupos experimentales de dosis alta y baja para determinar si la dosis alta es más efectiva que la dosis baja.
Manipulación del tratamiento. Los tratamientos son la característica única de la investigación experimental que diferencia este diseño de todos los demás métodos de investigación. La manipulación del tratamiento ayuda a controlar la «causa» en las relaciones causa-efecto. Naturalmente, la validez de la investigación experimental depende de lo bien que se haya manipulado el tratamiento. La manipulación del tratamiento debe comprobarse mediante pruebas previas y pruebas piloto antes del estudio experimental. Todas las mediciones realizadas antes de administrar el tratamiento se denominan medidas pretest , mientras que las realizadas después del tratamiento son medidas postest.
Selección y asignación aleatorias. La selección aleatoria es el proceso de extraer aleatoriamente una muestra de una población o de un marco de muestreo. Este enfoque se suele emplear en la investigación con encuestas y garantiza que cada unidad de la población tenga una probabilidad positiva de ser seleccionada en la muestra. La asignación aleatoria es, sin embargo, un proceso de asignación aleatoria de sujetos a grupos experimentales o de control. Se trata de una práctica habitual en la investigación experimental real para garantizar que los grupos de tratamiento sean similares (equivalentes) entre sí y con el grupo de control, antes de la administración del tratamiento. La selección aleatoria está relacionada con el muestreo y, por lo tanto, está más estrechamente relacionada con la validez externa (generalizabilidad) de los resultados. Sin embargo, la asignación aleatoria está relacionada con el diseño y, por tanto, está más relacionada con la validez interna. Es posible tener tanto la selección como la asignación aleatoria en una investigación experimental bien diseñada, pero la investigación cuasi-experimental no implica ni la selección ni la asignación aleatoria.
Amenazas a la validez interna. Aunque los diseños experimentales se consideran más rigurosos que otros métodos de investigación en cuanto a la validez interna de sus inferencias (en virtud de su capacidad para controlar las causas mediante la manipulación del tratamiento), no son inmunes a las amenazas a la validez interna. Algunas de estas amenazas a la validez interna se describen a continuación, en el contexto de un estudio del impacto de un programa especial de tutoría de recuperación de matemáticas para mejorar las habilidades matemáticas de los estudiantes de secundaria.
- La amenaza de la historia es la posibilidad de que los efectos observados (variables dependientes) sean causados por eventos extraños o históricos en lugar de por el tratamiento experimental. Por ejemplo, la mejora de la puntuación en matemáticas de los estudiantes después de la recuperación puede haber sido causada por su preparación para un examen de matemáticas en su escuela, en lugar del programa de recuperación de matemáticas.
- La amenaza de maduración se refiere a la posibilidad de que los efectos observados sean causados por la maduración natural de los sujetos (por ejemplo, una mejora general en su capacidad intelectual para comprender conceptos complejos) en lugar del tratamiento experimental.
- La amenaza de la prueba es una amenaza en los diseños pre-post en los que las respuestas de los sujetos en la prueba posterior están condicionadas por sus respuestas en la prueba previa. Por ejemplo, si los estudiantes recuerdan sus respuestas de la evaluación pretest, pueden tender a repetirlas en el examen postest. No realizar un pretest puede ayudar a evitar esta amenaza.
- La amenaza de instrumentación , que también se da en los diseños pre-post, se refiere a la posibilidad de que la diferencia entre las puntuaciones del pretest y del postest no se deba al programa de matemáticas de recuperación, sino a los cambios en el examen administrado, como que el postest tenga un grado de dificultad mayor o menor que el pretest.
- La amenaza de mortalidad se refiere a la posibilidad de que los sujetos abandonen el estudio en tasas diferenciales entre los grupos de tratamiento y de control debido a una razón sistemática, como que los abandonos fueran en su mayoría estudiantes que obtuvieron una puntuación baja en la prueba previa. Si los estudiantes de bajo rendimiento abandonan, los resultados de la prueba posterior estarán artificialmente inflados por la preponderancia de los estudiantes de alto rendimiento.
- La amenaza de regresión, también llamada regresión a la media, se refiere a la tendencia estadística del rendimiento general de un grupo en una medida durante una prueba posterior a retroceder hacia la media de esa medida en lugar de hacerlo en la dirección prevista. Por ejemplo, si los sujetos obtuvieron una puntuación alta en una prueba previa, tenderán a obtener una puntuación más baja en la prueba posterior (más cerca de la media) porque sus altas puntuaciones (alejadas de la media) durante la prueba previa fueron posiblemente una aberración estadística. Este problema tiende a ser más frecuente en las muestras no aleatorias y cuando las dos medidas están imperfectamente correlacionadas.
Diseños experimentales de dos grupos
Los diseños experimentales verdaderos más simples son los de dos grupos que implican un grupo de tratamiento y un grupo de control, y son ideales para probar los efectos de una única variable independiente que puede ser manipulada como tratamiento. Los dos diseños básicos de dos grupos son el diseño de grupo de control pretest-postest y el diseño de grupo de control postest, mientras que las variaciones pueden incluir diseños de covarianza. Estos diseños suelen representarse utilizando una notación de diseño estandarizada, en la que R representa la asignación aleatoria de los sujetos a los grupos, X representa el tratamiento administrado al grupo de tratamiento y O representa las observaciones pretest o postest de la variable dependiente (con diferentes subíndices para distinguir entre las observaciones pretest y postest de los grupos de tratamiento y control).
Diseño de grupo de control pretest-postest . En este diseño, los sujetos se asignan aleatoriamente a los grupos de tratamiento y control, se someten a una medición inicial (pretest) de las variables dependientes de interés, se administra al grupo de tratamiento un tratamiento (que representa la variable independiente de interés) y se miden de nuevo las variables dependientes (postest). La notación de este diseño se muestra en la Figura 10.1.

Figura 10.1. Diseño de grupo de control pretest-postest
El efecto E del tratamiento experimental en el diseño pretest postest se mide como la diferencia en las puntuaciones postest y pretest entre los grupos de tratamiento y control:
E = (O 2 – O 1 ) – (O 4 – O 3 )
El análisis estadístico de este diseño implica un simple análisis de la varianza (ANOVA) entre los grupos de tratamiento y control. El diseño pretest postest maneja varias amenazas a la validez interna, como la maduración, la prueba y la regresión, ya que se puede esperar que estas amenazas influyan en los grupos de tratamiento y de control de manera similar (aleatoria). La amenaza de selección se controla mediante la asignación aleatoria. Sin embargo, pueden existir otras amenazas para la validez interna. Por ejemplo, la mortalidad puede ser un problema si hay tasas de abandono diferenciales entre los dos grupos, y la medición del pretest puede sesgar la medición del postest (especialmente si el pretest introduce temas o contenidos inusuales).
Diseño de grupo de control de sólo postest . Este diseño es una versión más sencilla del diseño pretest-postest en la que se omiten las mediciones del pretest. La notación del diseño se muestra en la Figura 10.2.

Figura 10.2. Diseño de grupo de control sólo postest.
El efecto del tratamiento se mide simplemente como la diferencia en las puntuaciones postest entre los dos grupos:
E = (O 1 – O 2 )
El análisis estadístico apropiado de este diseño es también un análisis de varianza (ANOVA) de dos grupos. La simplicidad de este diseño lo hace más atractivo que el diseño pretest-postest en términos de validez interna. Este diseño controla la maduración, la prueba, la regresión, la selección y la interacción pretest-postest, aunque la amenaza de mortalidad puede seguir existiendo.
Diseños de covarianza . En ocasiones, las medidas de las variables dependientes pueden verse influidas por variables extrañas denominadas covariables . Las covariables son aquellas variables que no son de interés central para un estudio experimental, pero que, sin embargo, deben ser controladas en un diseño experimental para eliminar su efecto potencial sobre la variable dependiente y, por tanto, permitir una detección más precisa de los efectos de las variables independientes de interés. Los diseños experimentales analizados anteriormente no controlaban dichas covariables. Un diseño de covarianza (también llamado diseño de variables concomitantes) es un tipo especial de diseño de grupo de control pretest-postest en el que la medida pretest es esencialmente una medida de las covariables de interés en lugar de la de las variables dependientes. La notación del diseño se muestra en la Figura 10.3, donde C representa las covariables:

Figura 10.3. Diseño de covarianza
Debido a que la medida del pretest no es una medida de la variable dependiente, sino una covariable, el efecto del tratamiento se mide como la diferencia en las puntuaciones del postest entre los grupos de tratamiento y control como:
E = (O 1 – O 2 )
Debido a la presencia de covariables, el análisis estadístico correcto de este diseño es un análisis de covarianza de dos grupos (ANCOVA). Este diseño tiene todas las ventajas del diseño de sólo postest, pero con validez interna debido al control de las covariables. Los diseños de covarianza también pueden extenderse al diseño de grupo de control pretest-postest. 
Diseños factoriales
Los diseños de dos grupos son inadecuados si su investigación requiere la manipulación de dos o más variables independientes (tratamientos). En tales casos, necesitaría diseños de cuatro o más grupos. Estos diseños, muy populares en la investigación experimental, se denominan comúnmente diseños factoriales. Cada variable independiente en este diseño se llama factor, y cada subdivisión de un factor se llama nivel. Los diseños factoriales permiten al investigador examinar no sólo el efecto individual de cada tratamiento sobre las variables dependientes (denominados efectos principales), sino también su efecto conjunto (denominados efectos de interacción).
El diseño factorial más básico es un diseño factorial 2 x 2, que consiste en dos tratamientos, cada uno con dos niveles (como alto/bajo o presente/ausente). Por ejemplo, digamos que quiere comparar los resultados de aprendizaje de dos tipos diferentes de técnicas de instrucción (instrucción en clase y en línea), y también quiere examinar si estos efectos varían con el tiempo de instrucción (1,5 o 3 horas por semana). En este caso, tiene dos factores: el tipo de instrucción y el tiempo de instrucción; cada uno con dos niveles (en clase y en línea para el tipo de instrucción, y 1,5 y 3 horas/semana para el tiempo de instrucción), como se muestra en la Figura 8.1. Si desea añadir un tercer nivel de tiempo de instrucción (digamos 6 horas/semana), entonces el segundo factor constará de tres niveles y tendrá un diseño factorial 2 x 3. Por otra parte, si desea añadir un tercer factor, como el trabajo en grupo (presente frente a ausente), tendrá un diseño factorial 2 x 2 x 2. En esta notación, cada número representa un factor, y el valor de cada factor representa el número de niveles en ese factor.

Figura 10.4. Diseño factorial 2 x 2
Los diseños factoriales también pueden representarse utilizando una notación de diseño, como la que se muestra en el panel derecho de la Figura 10.4. R representa la asignación aleatoria de los sujetos a los grupos de tratamiento, X representa los propios grupos de tratamiento (los subíndices de X representan el nivel de cada factor), y O representa las observaciones de la variable dependiente. Observe que el diseño factorial 2 x 2 tendrá cuatro grupos de tratamiento, correspondientes a las cuatro combinaciones de los dos niveles de cada factor. En consecuencia, el diseño 2 x 3 tendrá seis grupos de tratamiento, y el diseño 2 x 2 x 2 tendrá ocho grupos de tratamiento. Como regla general, cada celda de un diseño factorial debe tener un tamaño de muestra mínimo de 20 (esta estimación se deriva de los cálculos de potencia de Cohen basados en tamaños de efecto medios). Así, un diseño factorial 2 x 2 x 2 requiere un tamaño de muestra total mínimo de 160 sujetos, con al menos 20 sujetos en cada celda. Como puede ver, el coste de la recogida de datos puede aumentar sustancialmente con más niveles o factores en su diseño factorial. A veces, debido a la limitación de recursos, algunas celdas de estos diseños factoriales pueden no recibir ningún tratamiento, lo que se denomina diseños factoriales incompletos. Dichos diseños incompletos perjudican nuestra capacidad para extraer inferencias sobre los factores incompletos.
En un diseño factorial, se dice que existe un efecto principal si la variable dependiente muestra una diferencia significativa entre múltiples niveles de un factor, en todos los niveles de otros factores. Ningún cambio en la variable dependiente a través de los niveles de los factores es el caso nulo (línea de base), a partir del cual se evalúan los efectos principales. En el ejemplo anterior, puede ver un efecto principal del tipo de instrucción, del tiempo de instrucción o de ambos sobre los resultados del aprendizaje. Existe un efecto de interacción cuando el efecto de las diferencias en un factor depende del nivel de un segundo factor. En nuestro ejemplo, si el efecto del tipo de instrucción en los resultados del aprendizaje es mayor para 3 horas/semana de tiempo de instrucción que para 1,5 horas/semana, entonces podemos decir que hay un efecto de interacción entre el tipo de instrucción y el tiempo de instrucción en los resultados del aprendizaje. Tenga en cuenta que la presencia de efectos de interacción domina y hace que los efectos principales sean irrelevantes, y no tiene sentido interpretar los efectos principales si los efectos de interacción son significativos.
Diseños experimentales híbridos
Los diseños híbridos son aquellos que se forman combinando características de diseños más establecidos. Tres de estos diseños híbridos son el diseño de bloques aleatorizados, el diseño de cuatro grupos de Salomón y el diseño de réplicas cambiadas.
Diseño de bloques aleatorizados. Se trata de una variación del diseño de grupo de control postest o pretest-postest en el que la población de sujetos puede agruparse en subgrupos relativamente homogéneos (llamados bloques ) dentro de los cuales se replica el experimento. Por ejemplo, si desea replicar el mismo diseño de sólo postest entre estudiantes universitarios y profesionales que trabajan a tiempo completo (dos bloques homogéneos), los sujetos de ambos bloques se dividen aleatoriamente entre el grupo de tratamiento (que recibe el mismo tratamiento) o el grupo de control (véase la figura 10.5). El propósito de este diseño es reducir el «ruido» o la varianza de los datos que puede atribuirse a las diferencias entre los bloques, de modo que el efecto real de interés pueda detectarse con mayor precisión.
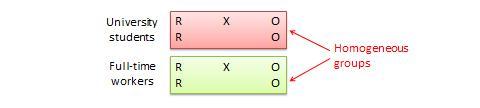
Figura 10.5. Diseño de bloques aleatorios.
Diseño de cuatro grupos de Salomón . En este diseño, la muestra se divide en dos grupos de tratamiento y dos grupos de control. Un grupo de tratamiento y un grupo de control reciben el pretest, y los otros dos grupos no. Este diseño representa una combinación de diseño de grupo de control de sólo postest y de pretest-postest, y está pensado para probar el potencial efecto de sesgo de la medición del pretest en las medidas del postest que tiende a ocurrir en los diseños de pretest-postest pero no en los diseños de sólo postest. La notación del diseño se muestra en la Figura 10.6.

Figura 10.6. Diseño de cuatro grupos de Solomon
Diseño de replicación conmutada . Se trata de un diseño de dos grupos implementado en dos fases con tres olas de medición. El grupo de tratamiento en la primera fase sirve como grupo de control en la segunda fase, y el grupo de control en la primera fase se convierte en el grupo de tratamiento en la segunda fase, como se ilustra en la Figura 10.7. En otras palabras, el diseño original se repite o replica temporalmente con los roles de tratamiento/control intercambiados entre los dos grupos. Al final del estudio, todos los participantes habrán recibido el tratamiento durante la primera o la segunda fase. Este diseño es más factible en contextos organizativos en los que los programas de la organización (por ejemplo, la formación de los empleados) se implementan por fases o se repiten a intervalos regulares.
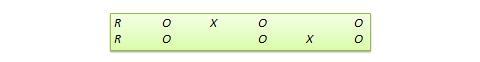
Figura 10.7. Diseño de replicación conmutada.
Diseños cuasi experimentales
Los diseños cuasi experimentales son casi idénticos a los verdaderos diseños experimentales, pero les falta un ingrediente clave: la asignación aleatoria. Por ejemplo, una sección entera de la clase o una organización se utiliza como grupo de tratamiento, mientras que otra sección de la misma clase o una organización diferente en la misma industria se utiliza como grupo de control. Esta falta de asignación aleatoria puede dar lugar a grupos no equivalentes, como por ejemplo que un grupo tenga un mayor dominio de un determinado contenido que el otro, por ejemplo por haber tenido un mejor profesor en un semestre anterior, lo que introduce la posibilidad de un sesgo de selección. Los diseños cuasi-experimentales son, por tanto, inferiores a los verdaderos diseños experimentales en cuanto a la validez del intervalo, debido a la presencia de una serie de amenazas relacionadas con la selección, como la amenaza de selección-maduración (los grupos de tratamiento y de control maduran a ritmos diferentes), la amenaza de selección-historia (los grupos de tratamiento y de control sufren un impacto diferencial por acontecimientos extraños o históricos), amenaza de selección-regresión (los grupos de tratamiento y de control retroceden hacia la media entre el pretest y el postest a ritmos diferentes), amenaza de selección-instrumentación (los grupos de tratamiento y de control responden de forma diferente a la medición), selección-prueba (los grupos de tratamiento y de control responden de forma diferente al pretest) y selección-mortalidad (los grupos de tratamiento y de control muestran tasas de abandono diferenciales). Dadas estas amenazas de selección, generalmente es preferible evitar los diseños cuasi-experimentales en la mayor medida posible.
Muchos diseños experimentales verdaderos pueden convertirse en diseños cuasi-experimentales omitiendo la asignación aleatoria. Por ejemplo, la versión cuasiequivalente del diseño de grupo de control pretest-postest se denomina diseño de grupos no equivalentes (NEGD), como se muestra en la Figura 10.8, con la asignación aleatoria R sustituida por la asignación no equivalente (no aleatoria) N . Asimismo, la versión cuasi experimental del diseño de replicación conmutada se denomina diseño de replicación conmutada no equivalente (véase la Figura 10.9).

Figura 10.8. Diseño NEGD.
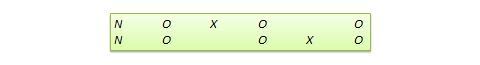
Figura 10.9. Diseño de replicación conmutada no equivalente.
Diseño de regresión-discontinuidad (RD) . Se trata de un diseño pretest-postest no equivalente en el que los sujetos se asignan al grupo de tratamiento o al de control en función de una puntuación de corte en una medida previa al programa. Por ejemplo, los pacientes que están gravemente enfermos pueden ser asignados a un grupo de tratamiento para probar la eficacia de un nuevo fármaco o protocolo de tratamiento y los que están levemente enfermos son asignados al grupo de control. En otro ejemplo, los estudiantes que van retrasados en las puntuaciones de los exámenes estandarizados pueden ser seleccionados para un programa curricular de recuperación destinado a mejorar su rendimiento, mientras que los que obtienen puntuaciones altas en dichos exámenes no son seleccionados para el programa de recuperación. La notación del diseño puede representarse como sigue, donde C representa la puntuación de corte:
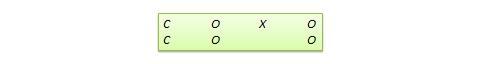
Figura 10.10. Diseño de DR.
Debido al uso de una puntuación de corte, es posible que los resultados observados sean una función de la puntuación de corte y no del tratamiento, lo que introduce una nueva amenaza para la validez interna. Sin embargo, el uso de la puntuación de corte también garantiza que los recursos limitados o costosos se distribuyan entre las personas que más los necesitan y no de forma aleatoria en una población, permitiendo al mismo tiempo un tratamiento cuasi-experimental. Las puntuaciones del grupo de control en el diseño RD no sirven como punto de referencia para comparar las puntuaciones del grupo de tratamiento, dada la no equivalencia sistemática entre los dos grupos. Más bien, si no hay discontinuidad entre las puntuaciones del pretest y el postest en el grupo de control, pero dicha discontinuidad persiste en el grupo de tratamiento, entonces esta discontinuidad se considera una prueba del efecto del tratamiento.
Diseño de pretest aproximado . Este diseño, que se muestra en la Figura 10.11, es muy similar al diseño NEGD estándar (pretest-postest), con una diferencia crítica: la puntuación del pretest se recoge después de la administración del tratamiento. Una aplicación típica de este diseño es cuando se trae a un investigador para que pruebe la eficacia de un programa (por ejemplo, un programa educativo) después de que el programa haya comenzado y los datos de la prueba previa no estén disponibles. En tales circunstancias, la mejor opción para el investigador suele ser utilizar una medida diferente pregrabada, como el promedio de calificaciones de los estudiantes antes del inicio del programa, como sustituto de los datos de la prueba previa. Una variación del diseño de la prueba previa indirecta es utilizar el recuerdo de los sujetos después de la prueba de los datos de la prueba previa, que puede estar sujeto a un sesgo de recuerdo, pero sin embargo puede proporcionar una medida de la ganancia percibida o el cambio en la variable dependiente.
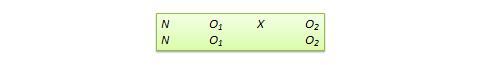
Figura 10.11. Diseño de pretest proxy.
Diseño de muestras pretest-postest separadas . Este diseño es útil si no es posible recoger datos de pretest y postest de los mismos sujetos por alguna razón. Como se muestra en la Figura 10.12, hay cuatro grupos en este diseño, pero dos grupos provienen de un único grupo no equivalente, mientras que los otros dos grupos provienen de un grupo no equivalente diferente. Por ejemplo, se quiere probar la satisfacción de los clientes con un nuevo servicio en línea que se implementa en una ciudad pero no en otra. En este caso, los clientes de la primera ciudad constituyen el grupo de tratamiento y los de la segunda el grupo de control. Si no es posible obtener medidas previas y posteriores de los mismos clientes, se puede medir la satisfacción del cliente en un momento dado, implementar el nuevo programa de servicio y medir la satisfacción del cliente (con un conjunto diferente de clientes) después de la implementación del programa. La satisfacción del cliente también se mide en el grupo de control en los mismos momentos que en el grupo de tratamiento, pero sin la implementación del nuevo programa. El diseño no es especialmente sólido, porque no se pueden examinar los cambios en la puntuación de satisfacción de ningún cliente específico antes y después de la implantación, sino que sólo se pueden examinar las puntuaciones medias de satisfacción de los clientes. A pesar de la menor validez interna, este diseño puede seguir siendo una forma útil de recopilar datos cuasi-experimentales cuando no se dispone de datos pretest y postest de los mismos sujetos.

Figura 10.12. Diseño de muestras separadas pretest-postest.
Diseño de variable dependiente no equivalente (NEDV) . Se trata de un diseño cuasi-experimental pre-post de un solo grupo con dos medidas de resultado, donde se espera teóricamente que una medida esté influenciada por el tratamiento y la otra no. Por ejemplo, si está diseñando un nuevo plan de estudios de cálculo para estudiantes de secundaria, es probable que este plan de estudios influya en las puntuaciones de cálculo de los estudiantes después de la prueba, pero no en las de álgebra. Sin embargo, las puntuaciones de álgebra después de la prueba pueden variar debido a factores externos como la historia o la maduración. Por lo tanto, las puntuaciones de álgebra anteriores a la prueba pueden utilizarse como medida de control, mientras que las de cálculo anteriores a la prueba pueden tratarse como medida de tratamiento. La notación del diseño, mostrada en la Figura 10.13, indica el grupo único mediante una sola N , seguida de la prueba previa O 1 y la prueba posterior O 2 para cálculo y álgebra para el mismo grupo de estudiantes. Este diseño es débil en cuanto a la validez interna, pero su ventaja radica en no tener que utilizar un grupo de control separado.
Una variación interesante del diseño NEDV es un diseño NEDV de coincidencia de patrones , que emplea múltiples variables de resultado y una teoría que explica en qué medida cada variable se verá afectada por el tratamiento. El investigador puede entonces examinar si la predicción teórica se corresponde con las observaciones reales. Esta técnica de emparejamiento de patrones, basada en el grado de correspondencia entre los patrones teóricos y los observados, es una forma poderosa de aliviar las preocupaciones de validez interna en el diseño NEDV original.
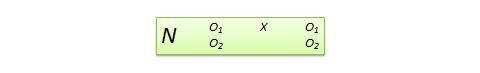
Figura 10.13. Diseño NEDV.
Peligros de la investigación experimental
La investigación experimental es uno de los diseños de investigación más difíciles, y no debe tomarse a la ligera. Este tipo de investigación suele ser el mejor con una multitud de problemas metodológicos. En primer lugar, aunque la investigación experimental requiere teorías para enmarcar las hipótesis que se pondrán a prueba, gran parte de la investigación experimental actual es ateórica. Sin teorías, las hipótesis que se prueban tienden a ser ad hoc, posiblemente ilógicas y sin sentido. En segundo lugar, muchos de los instrumentos de medición utilizados en la investigación experimental no se someten a pruebas de fiabilidad y validez, y no son comparables entre los distintos estudios. En consecuencia, los resultados generados con dichos instrumentos tampoco son comparables. En tercer lugar, muchas investigaciones experimentales utilizan diseños de investigación inadecuados, como variables dependientes irrelevantes, ausencia de efectos de interacción, ausencia de controles experimentales y estímulos no equivalentes entre los grupos de tratamiento. Los resultados de estos estudios tienden a carecer de validez interna y son muy sospechosos. En cuarto lugar, los tratamientos (tareas) utilizados en la investigación experimental pueden ser diversos, incomparables e inconsistentes entre los estudios y, a veces, inapropiados para la población de sujetos. Por ejemplo, a menudo se pide a los estudiantes universitarios que simulen ser directores de marketing y que realicen una compleja tarea de asignación de presupuestos en la que no tienen experiencia ni conocimientos. El uso de estas tareas inapropiadas, introduce nuevas amenazas a la validez interna (es decir, el rendimiento del sujeto puede ser un artefacto del contenido o la dificultad de la configuración de la tarea), genera hallazgos que no son interpretables y carecen de sentido, y hace imposible la integración de los hallazgos a través de los estudios.
El diseño de tratamientos experimentales adecuados es una tarea muy importante en el diseño experimental, porque el tratamiento es la razón de ser del método experimental, y nunca debe ser apresurado o descuidado. Para diseñar una tarea adecuada y apropiada, los investigadores deben utilizar tareas prevalidadas si están disponibles, realizar comprobaciones de manipulación del tratamiento para verificar la adecuación de dichas tareas (informando a los sujetos después de realizar la tarea asignada), realizar pruebas piloto (repetidas, si es necesario) y, en caso de duda, utilizar tareas más sencillas y familiares para la muestra de encuestados que tareas complejas o desconocidas.
En resumen, en este capítulo se han introducido conceptos clave en el método de investigación del diseño experimental y se han presentado diversos diseños experimentales y cuasi-experimentales reales. Aunque estos diseños varían ampliamente en cuanto a su validez interna, los diseños con menor validez interna no deben pasarse por alto y a veces pueden ser útiles bajo circunstancias específicas y contingencias empíricas.