El apilamiento de tolerancias, también conocido como apilamiento de tolerancias, se refiere a la combinación de varias tolerancias de dimensiones de piezas. Después de identificar una tolerancia en la dimensión de una pieza, es importante probar si esa tolerancia funcionaría con las tolerancias de la herramienta: el extremo superior o el extremo inferior. Una pieza o ensamblaje puede sufrir imprecisiones cuando sus tolerancias se apilan de forma incorrecta.
La importancia de las tolerancias
Las tolerancias influyen directamente en el coste y el rendimiento de un producto. Las tolerancias más ajustadas hacen que una pieza mecanizada sea más difícil de fabricar y, por tanto, suele ser más cara. Teniendo esto en cuenta, es importante encontrar un equilibrio entre la fabricabilidad de la pieza, su funcionalidad y su coste.
Consejos para el éxito del apilamiento de tolerancias
Evite el uso de tolerancias que sean innecesariamente pequeñas
Como se ha dicho anteriormente, las tolerancias más estrictas conducen a un mayor coste de fabricación ya que la pieza es más difícil de hacer. Este mayor coste se debe a menudo a la mayor cantidad de piezas desechadas que pueden producirse cuando las dimensiones se encuentran fuera de tolerancia. El coste de los portaherramientas de alta calidad y de las herramientas con tolerancias más estrictas también puede ser un gasto añadido.
Además, las tolerancias innecesariamente pequeñas conducirán a tiempos de fabricación más largos, ya que se realiza más trabajo para asegurar que la pieza cumple con los criterios estrictos durante el mecanizado, y después del mecanizado en el proceso de inspección.
Tenga cuidado de no sobredimensionar una pieza
Cuando se etiqueta una tolerancia superior e inferior en cada característica de una pieza, el sobredimensionamiento puede convertirse en un problema. Por ejemplo, una fresa de radio de esquina con radios de esquina derecha e izquierda podría tener una tolerancia de +/- 0,001″, y el plano entre ellos tiene una tolerancia de 0,002″. En este caso, la ventana de tolerancia para el diámetro de la fresa sería de +/- 0,004″, pero a menudo se calcula mal durante el dimensionamiento de la pieza. Además, la colocación de una tolerancia en esta llamada causaría que se sobredimensionara, y por lo tanto la dimensión de referencia «REF» debe dejarse para tomar el lugar de la tolerancia.
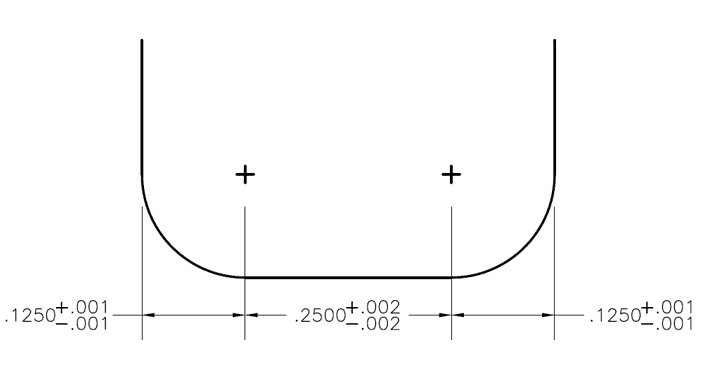
Figura 1: Forma de la ranura creada por una fresa de radio de esquina
Utilizar el análisis estadístico de tolerancias:
El análisis estadístico analiza la probabilidad de que las tres tolerancias estén por debajo o por encima de la anchura de la ranura dimensionada, basándose en una desviación estándar. Esta probabilidad está representada por una función de densidad de probabilidad normal, que puede verse en la figura 2 a continuación. Combinando todas las probabilidades de las diferentes piezas y dimensiones de un diseño, podemos determinar la probabilidad de que una pieza tenga un problema, o falle por completo, basándonos en las dimensiones y la tolerancia de las piezas. Generalmente este método de análisis sólo se utiliza para conjuntos con cuatro o más tolerancias.
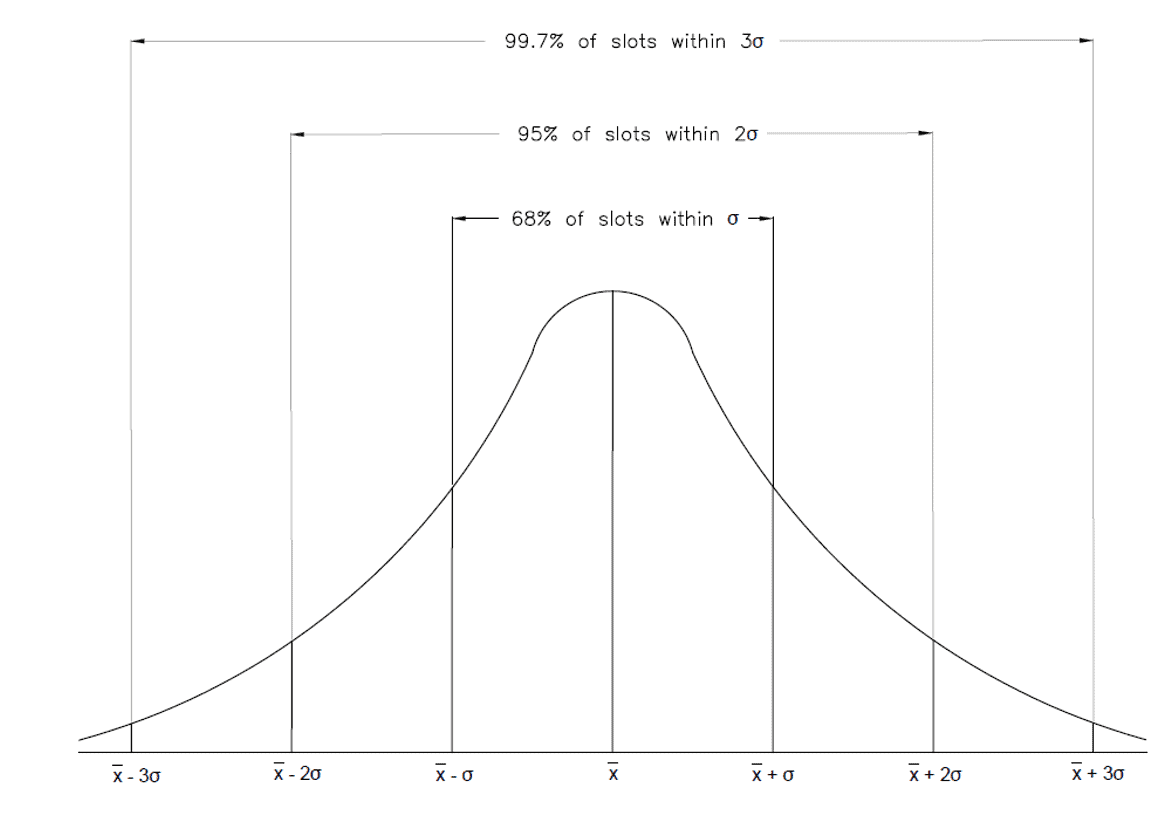
Figura 2: Apilamiento de tolerancias: Distribución normal
Antes de iniciar un análisis estadístico de tolerancias, debe calcular o elegir un factor de distribución de tolerancias. La distribución normal es 3 . Esto significa que la mayoría de los datos (o en este caso las tolerancias) estarán dentro de 3 desviaciones estándar de la media. Las desviaciones estándar de todas las tolerancias deben ser divididas por este factor de distribución de tolerancia para normalizarlas de una distribución de 3 a una distribución de 1 . Una vez hecho esto, se puede tomar la raíz de la suma al cuadrado para hallar la desviación estándar del conjunto.
Piensa en ello como si una taza de café se hiciera con 3 granos de diferente tamaño. Para hacer una deliciosa taza de café, primero hay que moler todos los granos del mismo tamaño para poder añadirlos al filtro de café. En este caso, los granos son las desviaciones estándar, el molinillo es el factor de distribución de la tolerancia y el filtro de café es la ecuación de la suma cuadrada de la raíz. Esto es necesario porque algunas tolerancias pueden tener diferentes factores de distribución basados en la estrechez del rango de tolerancia.
El método de análisis estadístico se utiliza si hay un requisito de que la ranura debe ser de 0,500″ de ancho con una tolerancia de +/- 0,003″, pero no hay necesidad de que los radios (,125″) y el plano (,250″) sean exactos siempre que encajen dentro de la ranura. En este ejemplo, tenemos 3 tolerancias bilaterales con sus desviaciones estándar ya disponibles. Como son bilaterales, la desviación estándar de la media sería simplemente el valor de la tolerancia + o -. Para los radios exteriores, esto sería 0,001″ y para la región plana media sería 0,002″.
Para este ejemplo, vamos a encontrar la desviación estándar (σ) de cada sección utilizando la ecuación 1. En esta ecuación representa la desviación estándar.
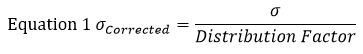
La suposición estándar es que la tolerancia de una pieza representa una distribución normal de +/- 3. Por lo tanto, el factor de distribución será 3. Utilizando la ecuación 1 en la sección izquierda de la figura 1, encontramos que su desviación estándar corregida equivale a:
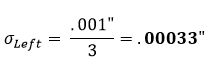
Esto se repite entonces para las secciones media y derecha:
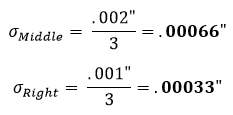
Después de llegar a estas desviaciones estándar, introducimos los resultados en la ecuación 2 para encontrar la desviación estándar de la zona de tolerancia. La ecuación 2 se conoce como la ecuación de la suma de la raíz al cuadrado.
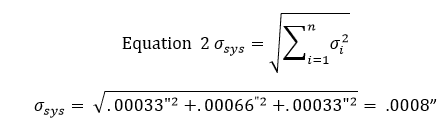
En este punto, significa que el 68% de las ranuras estarán dentro de una tolerancia de +/- .0008″. Si se multiplica esta tolerancia por 2 se obtendrá una ventana de confianza del 95%, mientras que si se multiplica por 3 se obtendrá una ventana de confianza del 99%.
68% de las ranuras estarán dentro de +/- .0008″
95% de las ranuras estarán dentro de +/- .0016″
99% de las ranuras estarán dentro de +/- .0024″
Estas ventanas de confianza son estándar para un conjunto de puntos de datos con distribución normal. Una distribución normal estándar puede verse en la Figura 2 de arriba.
El análisis estadístico de la tolerancia sólo debe utilizarse para conjuntos con más de 4 piezas toleradas. En este sencillo análisis no se han tenido en cuenta muchos factores. Este ejemplo era para 3 dimensiones bilaterales cuyas tolerancias eran representativas de sus desviaciones estándar de sus medias. En el análisis estadístico de tolerancia estándar, entran en juego otras variables como los ángulos, la excentricidad y el paralelismo, que requieren factores de corrección.
Utilice el análisis del peor caso:
El análisis del peor caso es la práctica de sumar todas las tolerancias de una pieza para encontrar la tolerancia total de la pieza. Al realizar este tipo de análisis, cada tolerancia se establece en su límite más grande o más pequeño en su rango respectivo. Esta tolerancia total puede entonces compararse con los límites de rendimiento de la pieza para asegurarse de que el conjunto está diseñado correctamente. Esto se utiliza típicamente para una sola dimensión (Sólo 1 plano, por lo tanto no hay ángulos involucrados) y para los conjuntos con un pequeño número de piezas.
El análisis del peor caso también se puede utilizar al elegir la herramienta de corte adecuada para su trabajo, ya que la tolerancia de la herramienta se puede añadir a la tolerancia de las piezas para un peor escenario. Una vez identificado este escenario, el maquinista o el ingeniero pueden realizar los ajustes adecuados para mantener la pieza dentro de las dimensiones especificadas en la impresión. Hay que tener en cuenta que el peor de los casos rara vez se da en la producción real. Aunque estos análisis pueden ser costosos para la fabricación, proporcionan tranquilidad a los maquinistas al garantizar que todos los conjuntos funcionarán correctamente. A menudo, este método requiere tolerancias estrictas porque el apilado total en condiciones máximas es la característica principal utilizada en el diseño. Las tolerancias más estrictas intensifican los costes de fabricación debido a la mayor cantidad de raspado, el tiempo de producción para la inspección y el coste del utillaje utilizado en estas piezas.
Ejemplo del peor caso en el contexto de la Figura 1:
Encuentra el límite inferior de la especificación.
Para el radio de la esquina izquierda
.125″ – .001″ = .124″
Para la sección plana
.250″ – .002″ = .248″
Para el radio de la esquina derecha
.125″ – .001″ = .124″
Suma todo esto al límite inferior de la especificación:
.124″ + .248″ + .124″ = .496″
Encuentra el límite superior de especificación:
Para el radio de la esquina izquierda