Objectivos de Aprendizagem
- Para utilizar gráficos para analisar a cinética de uma reacção.
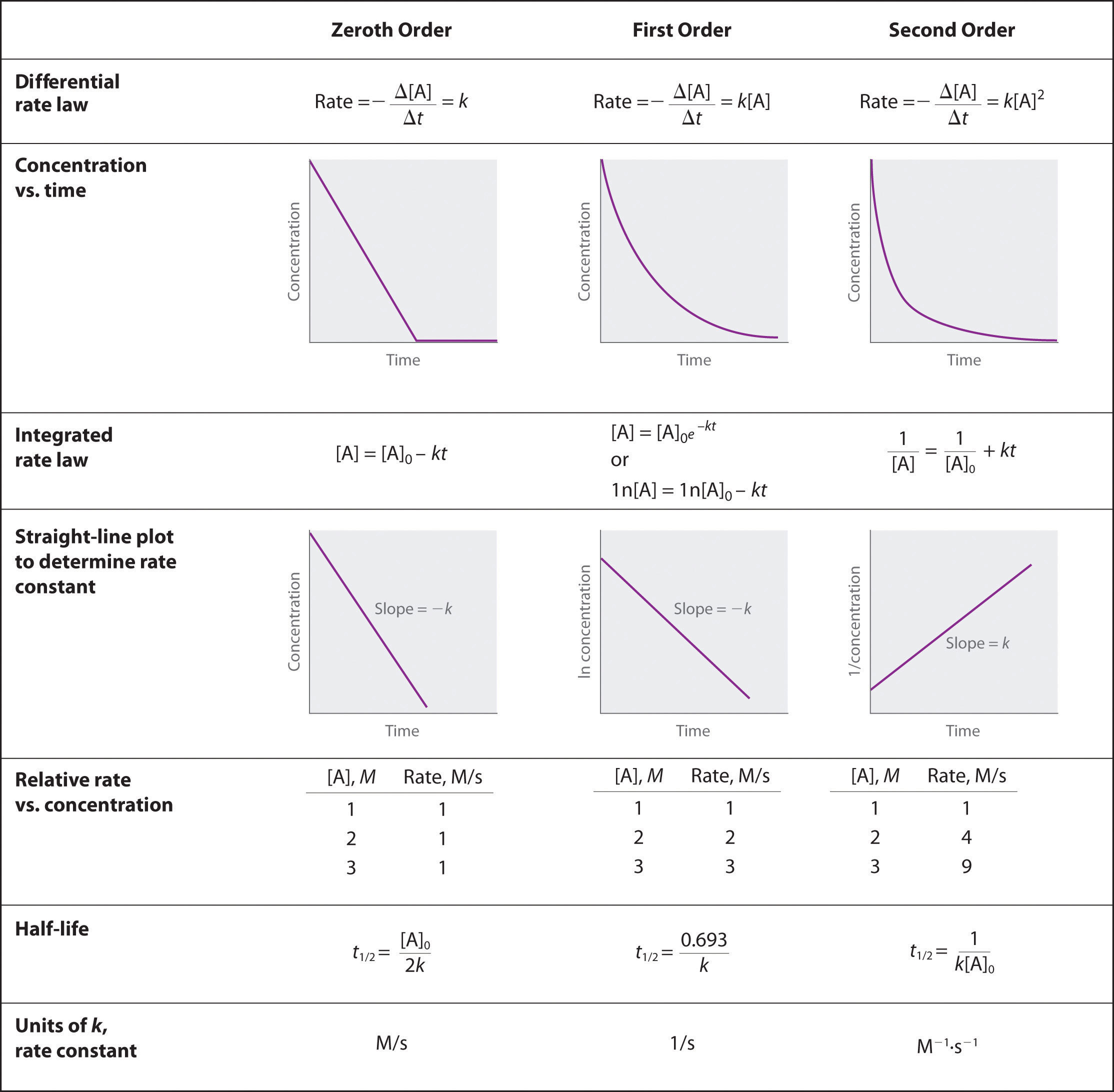
Aprendeu que a lei de taxa integrada para cada tipo comum de reacção (zeroth, primeira, ou segunda ordem num único reagente) pode ser traçada como uma linha recta. A utilização destas parcelas oferece uma alternativa aos métodos descritos para mostrar como a concentração do reagente muda com o tempo e determinar a ordem da reacção. Ilustraremos a utilização destes gráficos considerando a decomposição térmica do gás NO2 a temperaturas elevadas, que ocorre de acordo com a seguinte reacção:
\
Dados experimentais para esta reacção a 330°C estão listados na Tabela \PageIndex (1); são fornecidos como , ln, e 1/ versus tempo para corresponder às leis de taxa integrada para reacções de zeroth-, primeira, e segunda ordem, respectivamente.
| Time (s) | (M) | ln | 1/ (M-1) |
|---|---|---|---|
| 0 | 1.00 × 10-2 | -4.605 | 100 |
| 60 | 6.83 × 10-3 | -4.986 | 146 |
| 120 | 5.18 × 10-3 | -5.263 | 193 |
| 180 | 4.18 × 10-3 | -5.477 | 239 |
| 240 | 3.50 × 10-3 | -5.655 | 286 |
| 300 | 3.01 × 10-3 | -5.806 | 332 |
| 360 | 2,64 × 10-3 | -5.937 | 379 |
As concentrações reais de NO2 são traçadas versus tempo em parte (a) na Figura {1}(PageIndex{1}). Porque a parcela de versus t não é uma linha recta, sabemos que a reacção não é de ordem zerótica em NO2. Um gráfico de ln versus t (parte (b) na Figura \PageIndex{1}}) mostra-nos que a reacção não é de primeira ordem em NO2 porque uma reacção de primeira ordem daria uma linha recta. Tendo eliminado o comportamento de ordem zero e primeira ordem, construímos um gráfico de 1/ versus t (parte (c) na Figura \PageIndex{1})). Este gráfico é uma linha recta, indicando que a reacção é de segunda ordem em NO2.
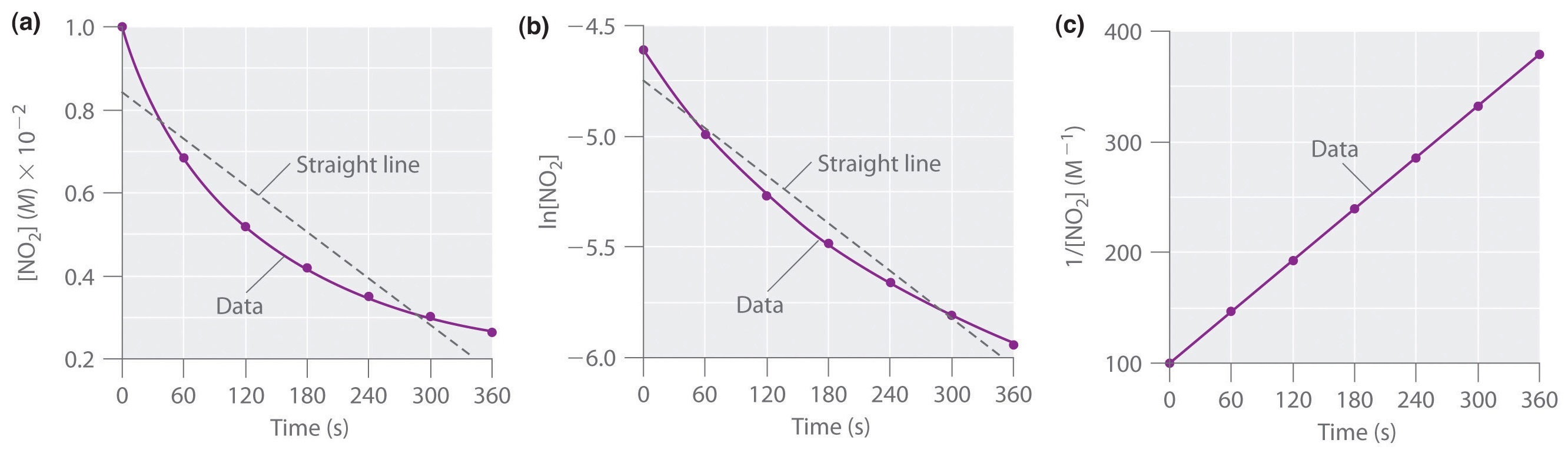
Acabámos de determinar a ordem de reacção utilizando dados de uma única experiência, traçando a concentração do reagente em função do tempo. Devido às formas características das linhas mostradas na Figura \PageIndex (2), os gráficos podem ser utilizados para determinar a ordem de reacção de uma reacção desconhecida. Em contraste, o método das taxas iniciais exigia múltiplas experiências a diferentes concentrações de NO2, bem como taxas iniciais precisas de reacção, que podem ser difíceis de obter para reacções rápidas.
Exemplo \\(\PageIndex{1})
p>Dinitrogen pentoxide (N2O5) decompõe-se em NO2 e O2 a temperaturas relativamente baixas na reacção seguinte:
\
Esta reacção é realizada numa solução de CCl4 a 45°C. As concentrações de N2O5 em função do tempo estão listadas na tabela seguinte, juntamente com os logaritmos naturais e as concentrações recíprocas de N2O5. Traçar um gráfico da concentração versus t, concentração ln versus t, e 1/concentração versus t e depois determinar a lei da taxa e calcular a constante da taxa.
| Time (s) | (M) | ln | 1/ (M-1) |
|---|---|---|---|
| 0 | 0.0365 | -3.310 | 27.4 |
| 600 | 0.0274 | -3.597 | 36.5 |
| 1200 | 0.0206 | -3.882 | 48.5 |
| 1800 | 0.0157 | -4.154 | 63.7 |
| 2400 | 0.0117 | -4.448 | 85.5 |
| 3000 | 0.00860 | -4.756 | 116 |
| 3600 | 0.00640 | -5.051 | 156 |
Dado: equação química equilibrada, tempos de reacção, e concentrações
Asked for: gráfico de dados, lei de taxas, e constante de taxas
Estratégia:
A Utilizar os dados da tabela para traçar separadamente a concentração, o logaritmo natural da concentração, e o recíproco da concentração (o eixo vertical) versus tempo (o eixo horizontal). Comparar os gráficos com os da Figura \PageIndex (1) para determinar a ordem da reacção.
B Escrever a lei da taxa para a reacção. Utilizando os dados apropriados da tabela e o gráfico linear correspondente à lei de taxa para a reacção, calcular a inclinação da linha traçada para obter a constante de taxa para a reacção.
Solução
A Aqui estão as parcelas de versus t, ln versus t, e 1/ versus t:
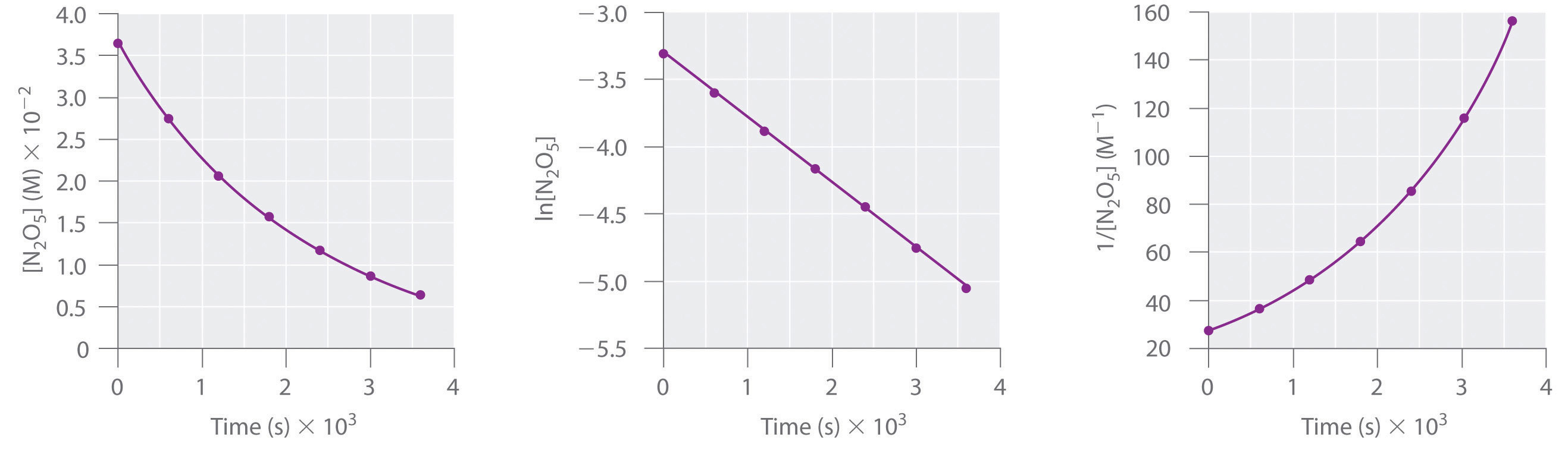
O gráfico de ln versus t dá uma linha recta, enquanto que as parcelas de versus t e 1/ versus t não dão. Isto significa que a decomposição de N2O5 é de primeira ordem em .
B A lei de taxa para a reacção é portanto
taxa = k
Calcular a constante de taxa é simples porque sabemos que a inclinação da parcela de ln versus t para uma reacção de primeira ordem é -k. Podemos calcular a inclinação usando quaisquer dois pontos que se encontrem na linha da parcela de ln versus t. Usando os pontos para t = 0 e 3000 s,
Thus k = 4,820 × 10-4 s-1.
Exercicio \(\PageIndex{1})
p>1,3-Butadieno (CH2=CH-CH=CH2; C4H6) é uma molécula orgânica volátil e reactiva utilizada na produção de borracha. Acima da temperatura ambiente, reage lentamente para formar produtos. As concentrações de C4H6 em função do tempo a 326°C estão listadas na tabela seguinte, juntamente com a ln e as concentrações recíprocas. Gráficos dos dados como concentração versus t, concentração ln versus t, e 1/concentração versus t. Em seguida, determinar a ordem de reacção em C4H6, a lei de taxas, e a constante de taxas para a reacção.
| Time (s) | (M) | ln | 1/ (M-1) |
|---|---|---|---|
| 0 | 1.72 × 10-2 | -4.063 | 58.1 |
| 900 | 1.43 × 10-2 | -4.247 | 69.9 |
| 1800 | 1.23 × 10-2 | -4.398 | 81.3 |
| 3600 | 9.52 × 10-3 | -4.398 | -4.398654 | 105 |
| 6000 | 7.30 × 10-3 | -4.920 | 137 |
Resposta
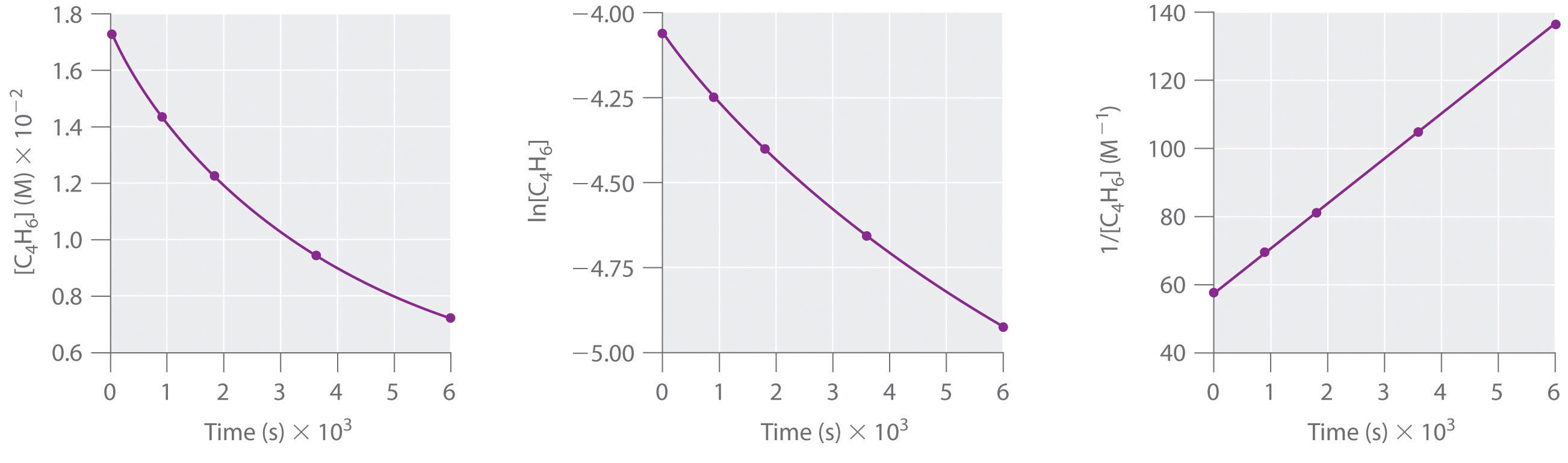
ordem de segundos em C4H6; taxa = k2; k = 1,3 × 10-2 M-1-s-1
Resumo
Para uma reacção de ordem zerot, um gráfico da concentração de qualquer reagente versus tempo é uma linha recta com um declive de -k. Para uma reacção de primeira ordem, um gráfico do logaritmo natural da concentração de um reagente versus tempo é uma linha recta com um declive de -k. Para uma reacção de segunda ordem, um gráfico do inverso da concentração de um reagente versus tempo é uma linha recta com uma inclinação de k.