Análise de Factores é um procedimento estatístico para descrever as inter-relações entre um número de variáveis observadas. A análise de factores é utilizada para medir variáveis que não podem ser medidas directamente, para resumir grandes quantidades de dados, e para desenvolver e testar teorias. Existem duas grandes categorias de análise de factores: exploratória e confirmatória. As técnicas de análise de factores exploratórios têm uma história muito mais longa do que as técnicas de análise de factores confirmatórios. As diferenças nas abordagens levam a diferentes utilizações (por exemplo, desenvolvimento teórico versus confirmação teórica).
Purposes
Análise de factores tem três objectivos fundamentais. Em primeiro lugar, é útil para medir construções que não podem ser prontamente observadas na natureza. Por exemplo, não podemos ouvir, ver, cheirar, provar, ou tocar a inteligência, mas pode ser inferido a partir da avaliação de variáveis observáveis, tais como o desempenho em testes de capacidade específica. A análise de factores também é útil no desenvolvimento de escalas para medir atitudes ou outras construções latentes, avaliando respostas a perguntas específicas. Em segundo lugar, a análise de factores é útil para resumir uma grande quantidade de observações num menor número de factores. Por exemplo, existem milhares de descritores de personalidade na língua inglesa. Através da análise de factores, os investigadores têm conseguido reduzir o número de factores distintos necessários para descrever a estrutura da personalidade. Em terceiro lugar, a análise de factores é útil para fornecer provas da validade da construção (por exemplo, validade factorial, convergente e discriminante). Por exemplo, se certas variáveis observáveis estiverem teoricamente relacionadas entre si, então a análise de factores deve demonstrar estas relações teóricas, demonstrando simultaneamente que as mesmas variáveis não estão razoavelmente relacionadas com variáveis de outros factores latentes. Todas estas três utilizações da análise de factores podem ser empregadas no desenvolvimento e teste de teorias psicológicas.
Modelo de Factores Básicos
O problema básico da análise de factores toma um número de variáveis observáveis e explica as suas inter-relações de uma forma análoga a uma equação de regressão. O modelo de factor comum é uma equação de regressão na qual os factores comuns actuam como preditores das variáveis X observadas. O modelo básico de factores é representado na Equação 1.
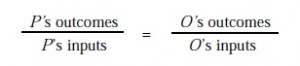
Nesta equação, X é a matriz das variáveis observadas, L é a matriz das cargas de factores ou pesos de regressão, f é a matriz dos factores comuns, e u é a matriz dos resíduos. O objectivo é explicar as inter-relações entre as variáveis X através dos factores comuns, f, e os termos de erro residual, chamados unicidade. A variância em X é dividida em componentes comuns e específicos. Ao contrário da regressão, porém, os preditores, f, são desconhecidos.
Para fornecer um exemplo fictício deste problema, suponha-se que se pede a vários supervisores que avaliem a relevância de seis características de personalidade para o desempenho efectivo do trabalho por parte dos subordinados. As características avaliadas são organizadas, sistemáticas, descuidadas, criativas,
intelectuais, e imaginativas. O quadro 1 apresenta a matriz de correlação hipotética para estas variáveis. O problema da análise de factores é explicar as relações entre estas variáveis com menos de seis factores latentes subjacentes. Organizadas, sistemáticas e descuidadas estão todas correlacionadas umas com as outras, mas não estão correlacionadas com criativas, intelectuais e imaginativas. Da mesma forma, criativo, intelectual e imaginativo estão todos correlacionados uns com os outros, mas não estão correlacionados com organizado, sistemático, e descuidado. Existem dois conjuntos de correlações que reflectem dois factores subjacentes.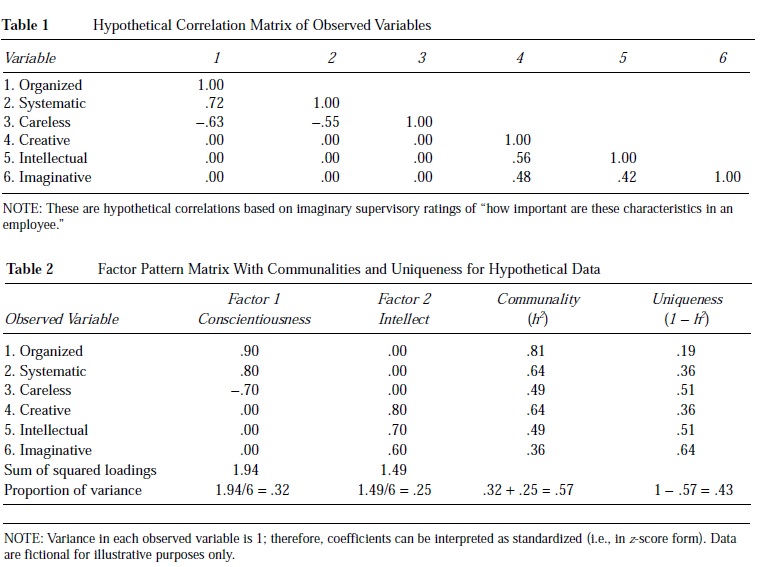
Quadro 2 representa a matriz de padrões de factores para estas variáveis e os factores latentes correspondentes. Os coeficientes de padrão no Quadro 2 (colunas 2 e 3) são as correlações das variáveis observadas com os factores. Matrizes de padrões ou de carregamento diferentes apresentarão tipos diferentes de correlações (por exemplo, correlações de Pearson, correlações parciais).
A comunalidade (h2) na coluna 4 do Quadro 2 representa a variância que a variável tem em comum com os factores que representa. A comunalidade é análoga a uma correlação múltipla ao quadrado em regressão. A singularidade na coluna 5 representa a variância específica de uma variável e não contabilizada pelo factor. A unicidade é análoga à variância residual na variável observada após a contabilização dos factores. As seis variáveis fictícias representam dois factores não observáveis, cada factor representando 36% a 81% da variância nas variáveis observadas.
Além da variância associada às variáveis observadas, a solução de análise de factores descreve a variância nos próprios factores. A soma das cargas ao quadrado (SSL) para um conjunto de variáveis descreve a variância de cada factor. Antes de qualquer transformação nos carregamentos de factores ter ocorrido, estes SSLs são chamados valores próprios. Idealmente, um pequeno número de factores será responsável por uma grande quantidade da variância nas variáveis observadas. A tabela 2 mostra que os factores representam 32% e 25%, para um total de 57% da variância nas variáveis observadas. Os restantes 43% da variância nas variáveis observadas não são comuns aos factores.
Análise de Factores Explicativos
Tipicamente, o objectivo da análise de factores exploratórios (AAE) é deixar os dados determinar as inter-relações entre um conjunto de variáveis. Embora um investigador que utilize AAE possa ter uma teoria que relacione as variáveis entre si, existem relativamente poucas restrições ao modelo de factor básico de uma AAE. Este tipo de análise tem sido útil no desenvolvimento e debate teórico há mais de um século.
Análise de factores explicativos é particularmente apropriada nas fases iniciais do desenvolvimento teórico e nas fases iniciais do desenvolvimento em escala ou teste. Em primeiro lugar, a AAE é útil na redução de dados quando as inter-relações entre variáveis não são especificadas de antemão. Um investigador que utiliza AAE faz uso do raciocínio indutivo, retirando uma série de observações e desenvolvendo a teoria a partir dessas observações. No exemplo das características dos funcionários com elevado desempenho, seis variáveis de personalidade foram, em última análise, reduzidas a dois factores. Para análises subsequentes, então, apenas duas variáveis precisam de ser discutidas, em vez das seis variáveis originais. A redução dos dados é particularmente útil para aliviar as preocupações de multicolinearidade (correlações demasiado elevadas) entre um conjunto de preditores. Um segundo benefício da AAE é a capacidade de detectar um factor geral. Quando são analisados vários testes de capacidade cognitiva específica, um factor geral tende a emergir, juntamente com vários factores específicos. Na avaliação da inteligência, por exemplo, todos os testes de capacidade correlacionam em certa medida com o factor geral de inteligência, ou g.
Finalmente, a AAE é particularmente útil na escala ou no desenvolvimento de testes porque permite ao investigador determinar a dimensionalidade do teste e detectar cargas cruzadas (correlações de variáveis com mais do que um factor). Os carregamentos cruzados não são geralmente desejáveis. No desenvolvimento em escala, é vantajoso ter itens que se relacionam apenas com um factor. Para o exemplo anterior, as três variáveis que representam a conscienciosidade não fazem cargas cruzadas sobre o intelecto e vice-versa.
Análise de Factores Confirmativos
O objectivo da análise de factores confirmativos (CFA) é testar hipóteses teoricamente derivadas, dado um conjunto de dados. O modelo de factor básico da Equação 1 ainda é relevante, mas são impostas certas restrições dado o modelo teórico particular que está a ser testado. Por exemplo, a partir do exemplo anterior, poder-se-ia usar CFA para impor restrições ao padrão de factores de modo a que não sejam permitidas cargas cruzadas. Desenvolvido durante os anos 60, o CFA é um desenvolvimento estatístico mais recente que o EFA (desenvolvido em 1904).
Análise do factor de confirmação é particularmente útil num processo de raciocínio dedutivo. É possível testar hipóteses específicas quando se utiliza CFA. Por exemplo, um investigador pode abordar o significado estatístico de cargas de factores individuais. No exemplo anterior, dada a correlação relativamente pequena, poder-se-ia determinar com certeza estatística o grau em que a variável observada, imaginativa, está correlacionada com o factor latente, intelecto.
Com CFA, é possível testar a hipótese de que dois factores versus apenas um factor (ou qualquer outra combinação numérica) estão subjacentes a um conjunto de dados. Na AAE, os investigadores confiam nas regras do polegar e da intuição, que podem desviar o investigador, mas na AAE, os modelos podem ser explicitamente comparados através de testes estatísticos de hipóteses nulas. Outra utilização do CFA é avaliar a equivalência de partes do modelo do factor básico dentro de um dado conjunto de dados. Por exemplo, pode fazer-se a hipótese de que todas as variáveis observadas para o intelecto estão igualmente relacionadas com o intelecto. Com CFA, a equivalência destas relações pode ser testada impondo restrições às cargas no modelo do factor básico (isto é, L na Equação 1).
É também importante determinar se os resultados de uma análise de factores são semelhantes entre grupos demográficos. A análise de factores confirmativa permite testar a invariância – isto é, a equivalência da estrutura dos factores, cargas, singularidades – entre diferentes grupos (por exemplo, étnico, sexo, cultural) de indivíduos. Um investigador pode estar interessado em saber se a mesma estrutura hipotética de factores surgiria se as respostas dos supervisores dos trabalhadores da indústria transformadora fossem comparadas com as respostas dos supervisores dos trabalhadores dos serviços. Pode acontecer que a variável observada não esteja relacionada com os factores latentes da mesma forma para os dois grupos. Por exemplo, a sistemática do indicador observado pode estar menos relacionada com a consciência do factor para os trabalhadores dos serviços do que para os trabalhadores da indústria transformadora. Num CFA que está a testar a equivalência de cargas de factores, um investigador pode testar a hipótese de que as correlações dos dois grupos são as mesmas ou diferentes.
A análise de factores confirmativa tem maior flexibilidade no controlo do que o EFA. Com CFA, alguns factores podem ser especificados como oblíquos (correlacionados uns com os outros), enquanto outros são especificados como ortogonais (não correlacionados uns com os outros). Dentro de uma única AAE, os factores são interpretados como oblíquos ou ortogonais, mas não como uma combinação dos dois. Além disso, a CFA permite ao investigador impor de forma flexível restrições adicionais sujeitas à teoria (por exemplo, permitindo uma singularidade correlacionada). Contudo, uma vantagem da AAE é que não são necessários tais constrangimentos teóricos ou especificações. Portanto, se não existirem, então a AAE pode ser uma melhor escolha.
- Gorsuch, R. L. (2003). Análise dos factores. Em J. A. Schinka & W. F. Velicer (Eds.), Handbook of psychology: Métodos de investigação em psicologia (Vol. 2, pp. 143-164). Hoboken, NJ: Wiley.
- Hurley, A. E., Scandura, T. A., Schriesheim, C. A., Brannick, M. T., Seers, A., Vandenberg, R. J., & Williams, L. J. (1997). Análise exploratória e confirmatória de factores: Orientações, questões, e alternativas. Journal of Organizational Behavior, 18, 667-683.
- Lance, C. E., & Vandenberg, R. J. (2002). Análise do factor de confirmação. Em F. Drasgow & N. Schmitt (Eds.), Measuring and analyzing behavior in organizations: Avanços na medição e análise de dados (pp. 221254). São Francisco: Jossey-Bass.
- Preacher, K. J., & MacCallum, R. C. (2003). Reparação da máquina de análise do factor eléctrico do Tom Swift. Understanding Statistics, 2, 13-43.
- Thompson, B. (2004). Análise exploratória e confirmatória de factores: Compreensão de conceitos e aplicações. Washington, DC: American Psychological Association.
- Vandenberg, R. J., & Lance, C. E. (2000). Uma revisão e síntese da literatura sobre invariância de medições: Sugestões, práticas, e recomendações para a investigação organizacional. Métodos de Investigação Organizacional, 3, 4-69.