Tolerance stacking, também conhecido como tolerance stack-up, refere-se à combinação de várias tolerâncias de dimensão de peças. Depois de uma tolerância ser identificada na dimensão de uma peça, é importante testar se essa tolerância funcionaria com as tolerâncias da ferramenta: ou a extremidade superior ou inferior. Uma peça ou montagem pode estar sujeita a imprecisões quando as suas tolerâncias são empilhadas incorrectamente.
A importância das tolerâncias
Tolerâncias influenciam directamente o custo e o desempenho de um produto. Tolerâncias mais apertadas tornam uma peça maquinada mais difícil de fabricar e, portanto, muitas vezes mais cara. Tendo isto em mente, é importante encontrar um equilíbrio entre a manufacturabilidade da peça, a sua funcionalidade e o seu custo.
Tips for Successful Tolerance Stacking
Avoid Using Tolerances that are Unnecessarily Small
Como foi dito acima, tolerâncias mais apertadas levam a um custo de fabrico mais elevado uma vez que a peça é mais difícil de fabricar. Este custo mais elevado deve-se frequentemente ao aumento da quantidade de peças sucateadas que podem ocorrer quando se verifica que as dimensões estão fora de tolerância. O custo de suportes de ferramentas de alta qualidade e de ferramentas com tolerâncias mais apertadas também pode ser uma despesa adicional.
Adicionalmente, tolerâncias desnecessariamente pequenas levarão a tempos de fabrico mais longos, à medida que mais trabalho é feito para assegurar que a peça cumpre critérios rigorosos durante a maquinagem, e após a maquinagem no processo de inspecção.
Sejam cuidadosos para não sobredimensionar uma peça
Quando uma tolerância superior e inferior é rotulada em cada característica de uma peça, o sobredimensionamento pode tornar-se um problema. Por exemplo, um moinho de ponta de canto com raios de canto direito e esquerdo pode ter uma tolerância de +/- .001″, e o plano entre eles tem uma tolerância de .002″. Neste caso, a janela de tolerância para o diâmetro da fresa seria de +/- .004″, mas é muitas vezes mal calculada durante o dimensionamento da peça. Além disso, a colocação de uma tolerância nesta chamada faria com que ela fosse sobredimensionada, pelo que a dimensão de referência “REF” deve ser deixada para ocupar o lugar da tolerância.
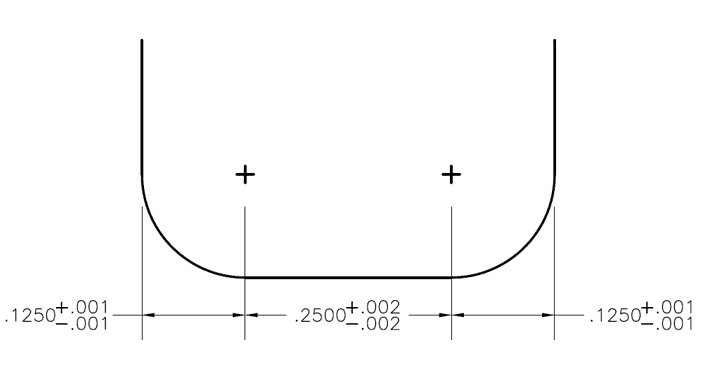p>Figure 1: Forma da ranhura criada por uma fresa de extremidade de raio de canto Análise de Tolerância Estatística de Utilização:
Análise estatística analisa a probabilidade de as três tolerâncias estarem abaixo ou acima da largura da ranhura dimensionada, com base num desvio padrão. Esta probabilidade é representada por uma função de densidade de probabilidade normal, que pode ser vista na figura 2 abaixo. Ao combinar todas as probabilidades das diferentes peças e dimensões num desenho, podemos determinar a probabilidade de uma peça ter um problema, ou falhar completamente, com base nas dimensões e tolerância das peças. Geralmente este método de análise só é utilizado para montagens com quatro ou mais tolerâncias.
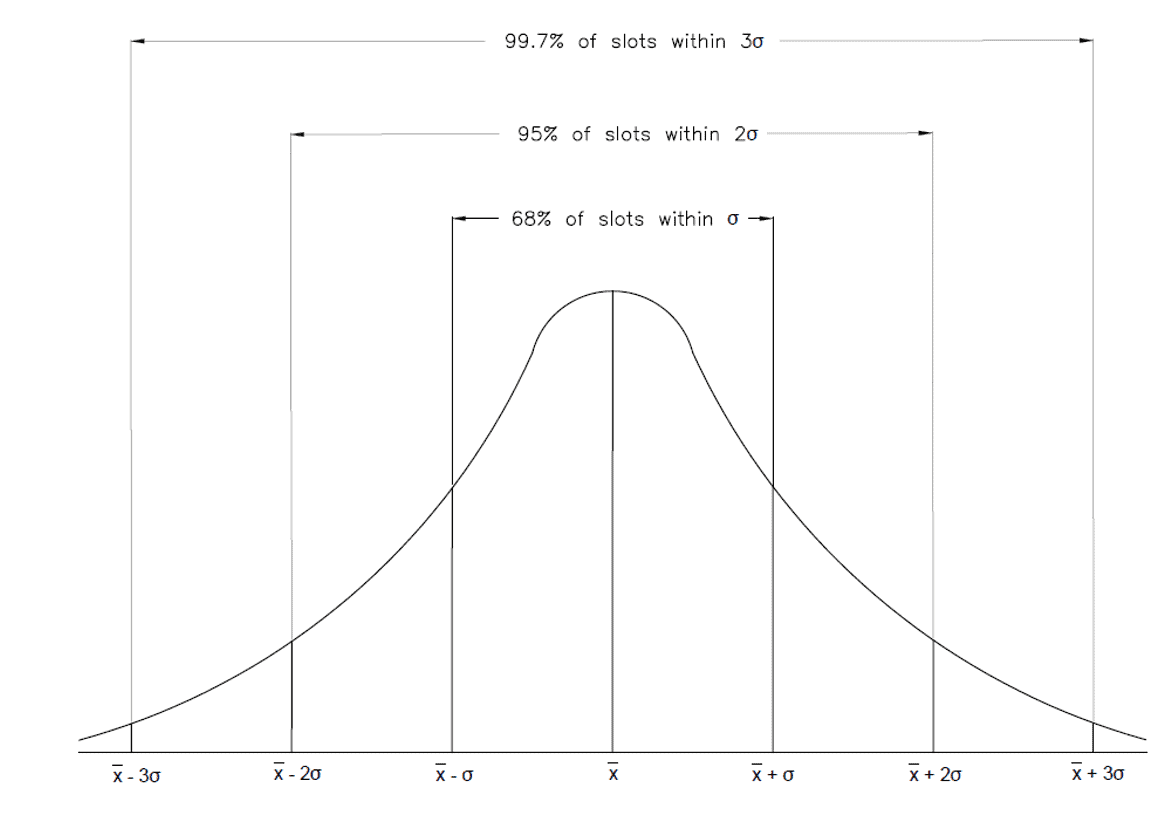
Figura 2: Empilhamento de Tolerância: Distribuição normal
Antes de iniciar uma análise de tolerância estatística, deve calcular ou escolher um factor de distribuição de tolerância. A distribuição padrão é de 3 . Isto significa que a maioria dos dados (ou neste caso tolerâncias) estará dentro de 3 desvios padrão da média. Os desvios padrão de todas as tolerâncias devem ser divididos por este factor de distribuição de tolerância para os normalizar de uma distribuição de 3 para uma distribuição de 1 . Uma vez feito isto, a soma da raiz ao quadrado pode ser tomada para encontrar o desvio padrão do conjunto.
p>Pense nisto como uma chávena de café a ser feita com 3 grãos de tamanho diferente. Para fazer uma deliciosa chávena de joe, é necessário moer primeiro todos os grãos no mesmo tamanho para que possam ser adicionados ao filtro de café. Neste caso, os grãos são os desvios padrão, o moinho é o factor de distribuição de tolerância, e o filtro de café é a equação da soma da raiz ao quadrado. Isto é necessário porque algumas tolerâncias podem ter diferentes factores de distribuição com base na estanquicidade do intervalo de tolerância.
O método de análise estatística é utilizado se houver a exigência de que a ranhura tenha uma largura de .500″ com uma tolerância de +/- .003″, mas não há necessidade de que os raios (.125″) e o plano (.250″) sejam exactos desde que encaixem dentro da ranhura. Neste exemplo, temos 3 tolerâncias bilaterais com os seus desvios padrão já disponíveis. Uma vez que são bilaterais, o desvio padrão da média seria simplesmente qualquer que seja o valor + ou – de tolerância. Para os raios exteriores, isto seria .001″ e para a região média plana isto seria .002″.
Para este exemplo, vamos encontrar o desvio padrão (σ) de cada secção usando a equação 1. Nesta equação representa o desvio-padrão.
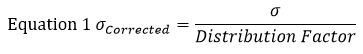
A suposição padrão é que uma tolerância de peça representa uma distribuição +/- 3 normal. Por conseguinte, o factor de distribuição será 3. Utilizando a equação 1 na secção esquerda da figura 1, verificamos que o seu desvio padrão corrigido equivale a:
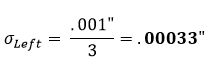
Isto é então repetido para as secções central e direita:
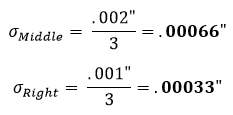
Após chegarmos a estes desvios padrão, introduzimos os resultados na equação 2 para encontrar o desvio padrão da zona de tolerância. A equação 2 é conhecida como a equação da soma raiz quadrada.
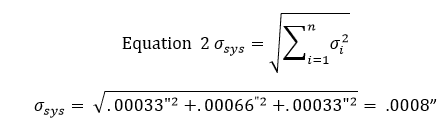
Neste ponto, significa que 68% das ranhuras estarão dentro de uma tolerância de +/- .0008″. Multiplicar esta tolerância por 2 resultará numa janela de confiança de 95%, onde multiplicá-la por 3 resultará numa janela de confiança de 99%.
68% das ranhuras estarão dentro de +/- .0008″
95% das ranhuras estarão dentro de +/- .0016″
99% das ranhuras estarão dentro de +/- .0024″
Estas janelas de confiança são padrão para um conjunto normal de pontos de dados distribuídos. Uma distribuição normal normal pode ser vista na Figura 2 acima.
Análise de tolerância estatística só deve ser utilizada para conjuntos com mais de 4 peças toleradas. Muitos factores não foram tidos em conta nesta análise simples. Este exemplo foi para 3 dimensões bilaterais cujas tolerâncias eram representativas dos seus desvios padrão em relação aos seus meios. Na análise de tolerância estatística padrão, outras variáveis entram em jogo, tais como ângulos, runout, e paralelismo, que requerem factores de correcção.
Use Worst Case Analysis:
Worst case analysis is the practice of adding up all the tolerances of a part to find the total part tolerance. Ao executar este tipo de análise, cada tolerância é definida para o seu maior ou menor limite na sua respectiva gama. Esta tolerância total pode então ser comparada com os limites de desempenho da peça para garantir que a montagem é concebida correctamente. Isto é tipicamente utilizado para apenas 1 dimensão (apenas 1 plano, portanto sem ângulos envolvidos) e para montagens com um pequeno número de peças.
Análise de caso perdido também pode ser utilizada ao escolher a ferramenta de corte apropriada para o seu trabalho, uma vez que a tolerância da ferramenta pode ser adicionada à tolerância das peças para um cenário de pior caso. Uma vez identificado este cenário, o maquinista ou engenheiro pode fazer os ajustes apropriados para manter a peça dentro das dimensões especificadas na impressão. Deve notar-se que o pior cenário raramente ocorre na produção real. Embora estas análises possam ser dispendiosas para o fabrico, proporciona tranquilidade aos maquinistas, garantindo que todas as montagens funcionarão correctamente. Muitas vezes este método requer tolerâncias apertadas porque o empilhamento total em condições máximas é a característica principal utilizada na concepção. Tolerâncias mais apertadas intensificam os custos de fabrico devido ao aumento da quantidade de raspagem, tempo de produção para inspecção, e custo de ferramentas utilizadas nestas peças.
Exemplo do pior cenário no contexto da Figura 1:
Conte o limite inferior de especificação.
Para o raio do canto esquerdo
.125″ – .001″ = .124″
Para a secção plana
.250″ – .002″ = .248″
Para o raio do canto direito
.125″ – .001″ = .124″
Adicionar todos estes juntos ao limite inferior de especificação:
.124″ + .248″ + .124″ = .496″
Limite de especificação superior:
Para o raio do canto esquerdo