A quarta dimensão é um lugar para onde se pode viajar, indo numa direcção perpendicular à terceira dimensão. Para o olho destreinado, esta afirmação não faz absolutamente nenhum sentido. Como poderia haver uma direcção que seja perpendicular a um espaço tridimensional? A fim de melhor compreender este conceito, temos de trabalhar lentamente em todas as dimensões e analisar que mudanças estão a ser feitas entre cada uma.

Zeroth Dimension
A dimensão zeroth é aquela em que não pensamos muitas vezes. Os pontos são os únicos seres dimensionais que podem ser correctamente compreendidos na dimensão zeroth. Eles não têm absolutamente nenhuma dimensão, nenhuma largura, nenhum comprimento, nenhuma altura. São os mais pequenos que alguma vez poderiam ser, mas também os maiores que poderiam ser ao mesmo tempo.
Como procuramos aprofundar a nossa compreensão da quarta dimensão. Podemos examinar um cubo em cada dimensão à medida que progredimos. Um cubo na dimensão zeroth seria simplesmente um ponto. Todas as suas dimensões são as mesmas em todas as direcções porque não há nenhuma. O cubo ainda representa um ponto no espaço, mas essa é a extensão do seu poder na dimensão zeroth. Agora, vamos avançar para 1-D.
Primeira dimensão
A transição entre a dimensão zeroth e a primeira dimensão envolve uma extrusão em qualquer direcção. Na primeira dimensão, tudo existe como uma linha. A única coisa que difere entre os objectos na primeira dimensão é o seu comprimento. Todas as linhas têm a mesma largura e a mesma altura, mas o seu comprimento pode ser variado.
Se quiser fazer linhas com espessuras variáveis, então tem de se mover para linhas bidimensionais. Um cubo na primeira dimensão pareceria uma linha com o mesmo comprimento do referido cubo, mas sem valores de largura ou altura.
Segunda dimensão
Transformar um segmento de linha numa direcção perpendicular à direcção 1-dimensional leva-o para a segunda dimensão. Tenha esta ideia em mente à medida que expandimos o nosso conhecimento dimensional e reparamos nesta acção perpendicular repetida à medida que nos movemos através das dimensões.
Na segunda dimensão, o nosso cubo pode começar a parecer-se com um cubo, mas apenas por pouco. Um cubo existiria como um quadrado na segunda dimensão. Pode-se, claro, desenhar uma representação de um cubo 3D em 2 dimensões, mas não é assim que um cubo se pareceria em 2 dimensões. Pelo contrário, isto seria simplesmente uma representação da terceira dimensão sobreposta à segunda.
Comprimento e largura podem ser variados na segunda dimensão, o que permite formas e geometria básicas. Quando avançamos para a terceira dimensão, a matemática começa a tornar-se mais complexa.
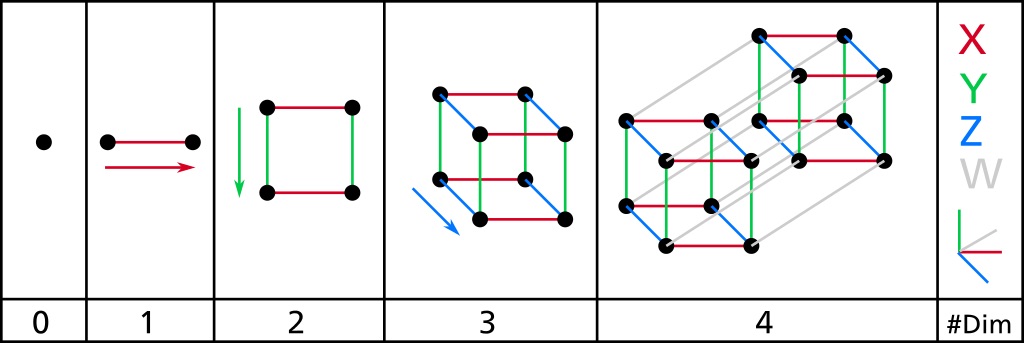
Terceira dimensão
O cubo da segunda dimensão é agora extrudido numa terceira direcção perpendicular a ambos os lados do quadrado 2D. Para colocar isto em termos cartesianos, o quadrado 2D existia nas direcções X e Y. Passando para a terceira dimensão, extrude-se esse quadrado na direcção Z. A terceira dimensão é onde o nosso cubo se torna de facto um cubo no nosso sentido tradicional definido. O objecto tem dimensões de largura, comprimento, e altura.
Através de todas as dimensões, é importante notar que um cubo irá manter todas as suas propriedades básicas em teoria. Todos os ângulos serão rectos e todos os lados serão os mesmos. Introduzindo outro princípio de dimensões, podemos examinar o que ocorreria se o cubo fosse expandido indefinidamente. Quando um cubo na terceira dimensão é expandido ao infinito, ele engloba a totalidade do espaço tridimensional.
Até agora, é provável que se deva compreender estas 3 dimensões, afinal, são as dimensões com as quais mais frequentemente nos associamos.
Quarta Dimensão
Quando trazemos o cubo para a quarta dimensão, começamos a experimentar alguma matemática contraintuitiva. Extruímos o cubo numa direcção perpendicular a todas as três primeiras. Isto é impossível dentro da terceira dimensão, porque existem apenas 3 dimensões nas quais o cubo já está expandido. Quando adicionamos a quarta dimensão, para manter as propriedades do cubo de todos os ângulos sendo 90 graus e sendo todos os lados iguais, temos de extrudir nesta nova dimensão.
Cubos na quarta dimensão são tecnicamente chamados tesseracts. Os objectos em 4D diferem em comprimento, largura, altura e comprimento. A sobreposição do comprimento em qualquer das dimensões anteriores dá a um objecto nas dimensões seguintes um comprimento 0, ou um valor infinitamente pequeno.
Todos os bordos de um tesseract são iguais, e todos os ângulos são rectos. Isto faz sentido em teoria, mas quando começamos a imaginar como seria um tesseract, ficamos presos pelas nossas mentes tridimensionais. Para ver um tesseract, temos de sobrepor este objecto tesseract na terceira dimensão.
A principal forma de representarmos um tesseract, ou cubo na quarta dimensão, é projectando-o na terceira dimensão com perspectiva. Esta representação pode ser vista abaixo.
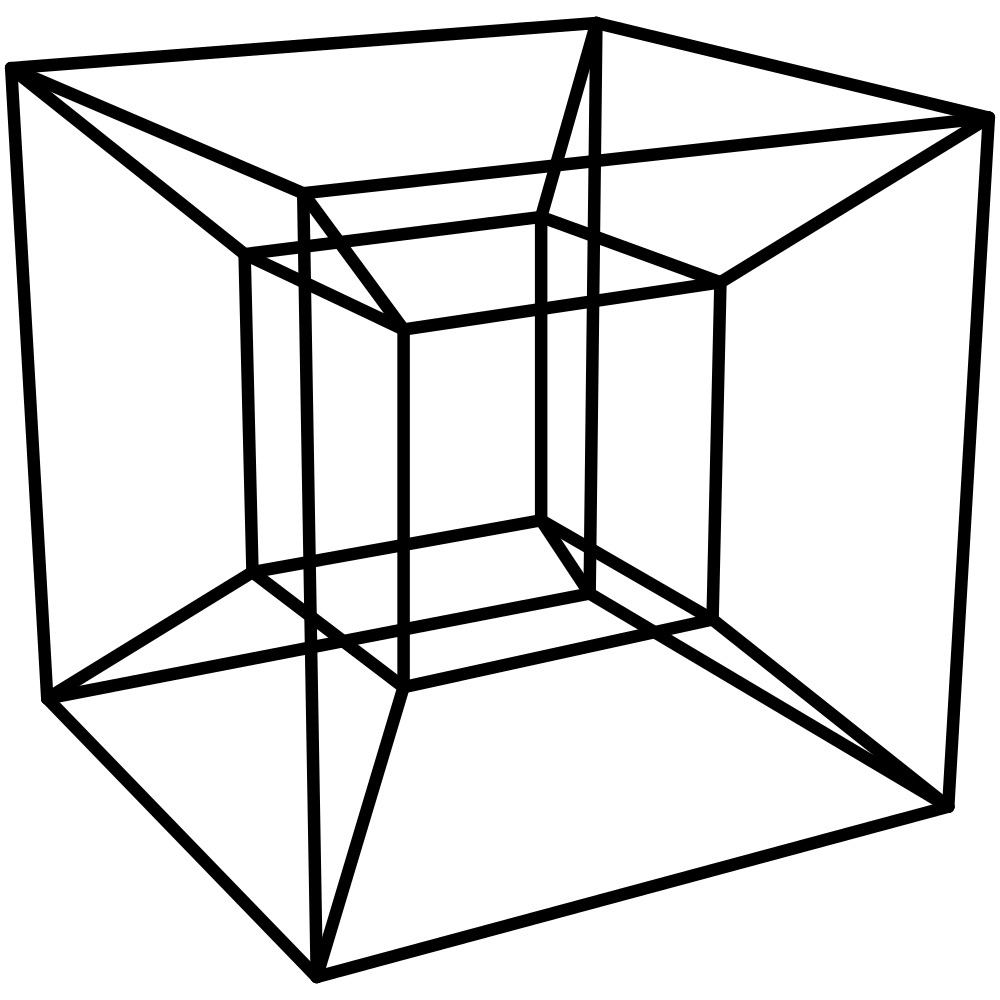
Esta é também uma representação em perspectiva de um tesseract na forma gif.

Esta representação não é o aspecto de um cubo 4D, é simplesmente o que se parece em perspectiva visto da terceira dimensão. Para resumir a nossa compreensão da quarta dimensão, os objectos em 4D variam em valor por comprimento, largura, altura e comprimento. Todas estas medidas dimensionais estendem-se numa direcção perpendicular às três anteriores. A largura é perpendicular ao comprimento, a altura é perpendicular à largura e ao comprimento, e finalmente, o comprimento é perpedicular à altura, ao comprimento, e à largura.
Estes conceitos são difíceis de compreender mas, esperemos, isto dá-lhe uma boa compreensão geral de como funciona a quarta dimensão e como a interpretamos a partir dos nossos olhos tridimensionais.
P>P>P>Painda não faz qualquer sentido? Deixe que Carl Sagan lhe explique.