Ever gráficos que parecem iguais, mas um é mais esticado verticalmente do que o outro? Tudo isto graças à técnica de transformação a que chamamos estiramento vertical.
Estiramento vertical num gráfico puxará o gráfico original para fora por um determinado factor de escala.
Quando uma função de base é multiplicada por um determinado factor, podemos imediatamente fazer o gráfico da nova função aplicando o estiramento vertical.
Antes de mergulharmos mais fundo nesta técnica de transformação, é melhor rever os seus conhecimentos sobre os seguintes tópicos:
- Ubviamente, compreender as funções parentais comuns que poderemos encontrar.
- Refresca os seus conhecimentos sobre as transformações verticais e horizontais.
Fique à vontade para clicar nos links para refrescar os seus conhecimentos sobre estes tópicos essenciais. Vamos agora discutir a terceira técnica de transformação: estiramento vertical.
O que é um estiramento vertical?
Estiramento vertical ocorre quando um gráfico de base é multiplicado por um determinado factor superior a 1, o que resulta no gráfico ser puxado para fora mas mantendo os valores de entrada (ou x). Quando uma função é esticada verticalmente, esperamos que os valores y do seu gráfico estejam mais afastados do eixo x.
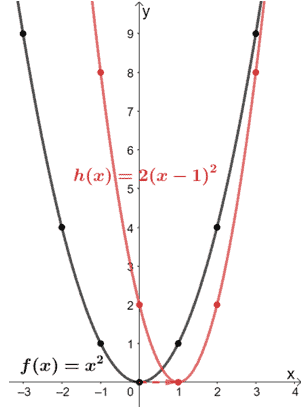
O gráfico abaixo mostra o gráfico de f(x) e as suas transformações. Porque não observamos como f(x) é transformado quando multiplicamos os valores de saída por um factor de 3 e 6?
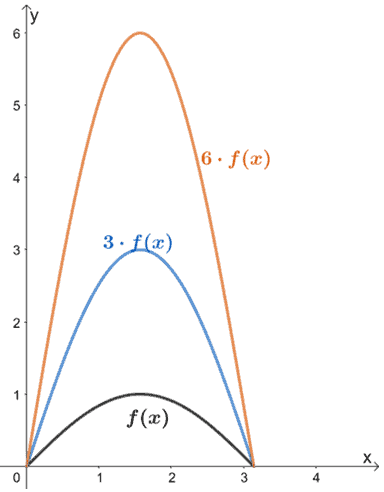
Quando f(x) é multiplicado por factores de escala de 3 e 6, o seu gráfico estica-se pelos mesmos factores de escala. Também podemos ver que os seus valores de entrada (x para este caso) permanecem os mesmos; apenas os valores para y foram afectados quando esticamos f(x) verticalmente.
Como generalizamos esta regra? Quando temos |a| > 1, a – f(x) irá esticar a função base por um factor de escala de a. Os valores de entrada permanecerão os mesmos, portanto os pontos de coordenadas do gráfico serão agora (x, ay).
Isto significa que se f(x) = 5x + 1 é esticado verticalmente por um factor de 5, a nova função será equivalente a 5 – f(x). Assim, a função resultante é 5(5x + 1) = 25x + 5.
Como esticar verticalmente uma função?
Quando se dá o gráfico de uma função, podemos esticá-la verticalmente puxando a curva para fora com base no factor de escala dado. Eis algumas coisas a lembrar quando esticamos verticalmente funções:
- Segurar que os valores para x permanecem os mesmos, para que a base da curva não mude.
- Isto significa que ao aplicar estiramentos verticais sobre um gráfico de base, os seus intercepção x permanecerão os mesmos.
- Tome nota dos novos pontos críticos, tais como o novo ponto máximo do gráfico.
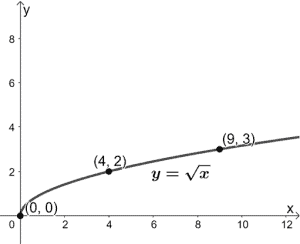
Porque não tentamos esticar verticalmente a função y = √x por um factor de 2?
Incluímos alguns pontos-guia realçando como também mudam quando fazemos o gráfico da nova função y = 2√x. O que é que esperamos do novo gráfico?
, ainda vai começar na origem, as coordenadas y vão aumentar por um factor de 2, e o gráfico vai esticar-se por um factor de 2.
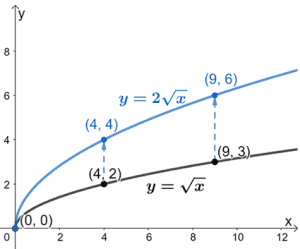
O gráfico acima mostra como podemos esticar verticalmente o gráfico de y =√x por um factor de 2 ao gráfico y = 2√x também.
Podemos aplicar o mesmo processo ao esticar verticalmente diferentes tipos de funções e gráficos. Antes de tentarmos outros exemplos, porque não resumimos o que aprendemos até agora sobre estiramento vertical?
Resumo da definição e propriedades do estiramento vertical
Agora aprendemos sobre o efeito de escalar uma função por um factor positivo, a. Abaixo estão alguns indicadores importantes a lembrar quando lidamos com estiramentos verticais nos gráficos:
- Um estiramento vertical ocorre apenas quando o factor de escala é superior a 1.
- Transporte as coordenadas y para o mesmo factor de escala.
- Retenha a posição dos interceptores x.
- A função estiramento vertical terá o mesmo domínio e uma nova gama.
Vamos manter estes avisos úteis em mente quando resolvermos as questões após esta secção. Pronto? Vamos começar a aplicar esta técnica de transformação!
Exemplo 1
A função, g(x), é obtida por estiramento vertical f(x) = x2 + 1 por um factor de escala de 3. Qual das seguintes é a expressão correcta para g(x)?
- g(x) = 3×2 + 1
- g(x) = x2 + 3
- g(x) = 3×2 + 3
- g(x) = 3(x + 1)2
Solução
Quando esticamos uma função verticalmente, multiplicamos a função de base pelo seu factor de escala. Assim, temos g(x) = 3 – f(x). Vamos certificar-nos de distribuir 3 a cada um dos termos em f(x).
g(x) = 3(x2 + 1)
==3×2 + 3
Isto significa que a expressão correcta para g(x) é 3×2 + 3.
Exemplo 2
A tabela de valores para f(x) é mostrada abaixo. Se g(x) = 4-f(x), construir uma tabela de valores para a função g(x).
| x | -6 | -4 | -2 | 2 | 4 | 6 |
| f(x) | 9 | 4 | 1 | 1 | 4 | 9 |
Solução
Desde g(x) = 4-f(x), a função g(x) é esticada verticalmente por um factor de escala de 4. O que é que isto significa para a sua tabela de valores? 9 =
Multiplicamos cada valor de f(x) por 4 para encontrar os valores de saída para g(x). Note-se que os valores para as coordenadas-x permanecerão os mesmos.
| x | -6 | -4 | -2 | 2 | 4 | 6 |
| g(x) | 36 | 16 | 4 | 4 | 16 | 36 |
Exemplo 3
Preencher os espaços em branco para que as seguintes afirmações sejam verdadeiras, dado que f(x) = |x|.
- Se g(x) = 4|x|, a função g(x) é esticada verticalmente por um factor de escala de ________.
- Se o gráfico de f(x) é esticado verticalmente por um factor de 2 para atingir h(x), então h(x) = ___ ∙ f(x).
- Se o gráfico de f(x) for esticado verticalmente por um factor 3, a expressão para h(x) é ________.
Solução
- Comparando g(x) e f(x), temos g(x) = 4 ∙ f(x). Isto significa que a função g(x) é esticada verticalmente por um factor de 4.
- esticar f(x) verticalmente por um factor de 2 resultará em h(x) ser igual a 2 vezes f(x).
- Esticar f(x) verticalmente por um factor de 3 resultará em h(x) ser igual a 3 vezes f(x). Assim, h(x) = 3|x|.
Exemplo 4
Observar as duas funções mostradas abaixo e relacionar h(x) com g(x).
p>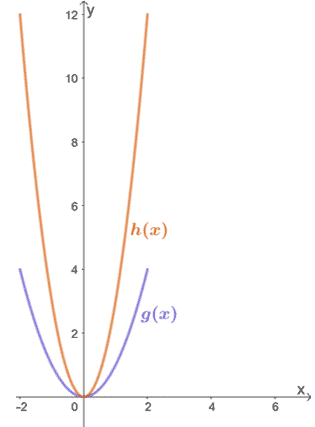
Solução
Apenas por inspecção, podemos ver que h(x) resulta do estiramento vertical de g(x). Para encontrar o factor pelo qual h(x) foi esticado, vamos inspeccionar alguns valores correspondentes para g(x) → h(x).
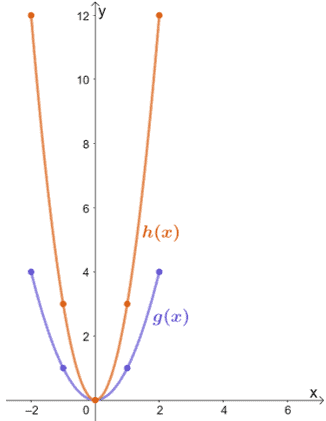
- (0, 0) → (0, 0)
- (1, 1) → (1, 3)
- (2, 4) → (1, 12)
Vemos que a coordenada y de h(x) é três vezes a de g(x) para cada par de pontos. Isto significa que h(x) = 3 ∙ g(x), portanto h(x) é o resultado de g(x) ser esticado verticalmente por um factor de escala de 3,
Exemplo 5
A função, A(x), modela a distância (em km) percorrida pelo carro A durante um período de tempo (em horas).
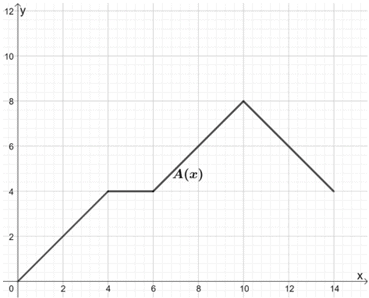
Jack quis comparar este modelo com B(x), cujo movimento segue o mesmo padrão, mas o carro observado pode cobrir duas vezes a distância de A(x). Use o gráfico de A(x) para esboçar o gráfico de B(x).
Solução
Desde B(x) = 2 ∙ A(x), esticamos verticalmente o gráfico de A(x) por um factor de escala de 2.
Para isso, podemos tomar nota de alguns pontos do gráfico e encontrar os seus valores correspondentes para B(x). Para encontrar os novos pares encomendados, vamos multiplicar cada y-coordenado por 2,
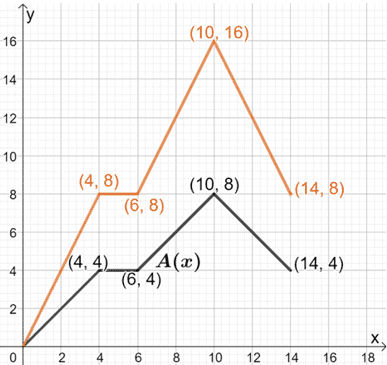
Podemos ligar estes pontos para formar B(x). Tenha em mente que a forma de A(x) e a sua base devem permanecer as mesmas.
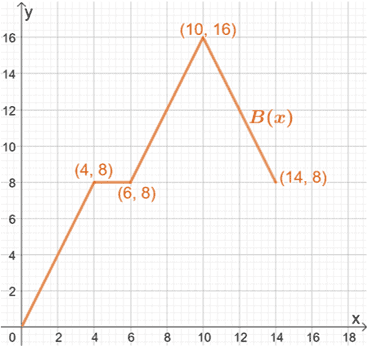
Hence, temos o gráfico final para B(x), como mostrado acima.
Exemplo 6
Observar as duas funções mostradas abaixo e relacionar h(x) com g(x). Qual é a expressão para h(x)?
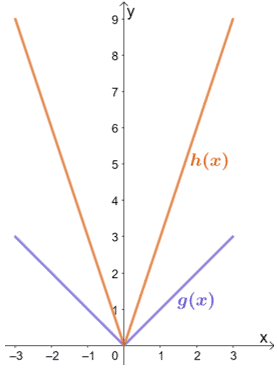
Solução
Vemos que h(x) é o resultado de g(x) é esticado verticalmente por um determinado factor de escala. Vamos em frente e inspeccionar alguns dos pontos correspondentes.
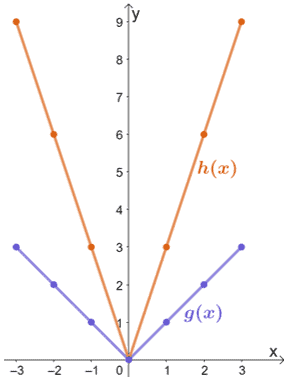
- (-3, 3) → (-3, 9)
- (-1, 1) → (-1, 3)
- (0, 0) → (0, 0)
- (1, 1) → (1, 3)
- (3, 3) → (3, 9)
A partir disto, podemos ver que quando g(x) é esticado verticalmente por um factor de escala de 3, o gráfico resultante será o de h(x). Assim, temos h(x) = 3 ∙ g(x).
A função g(x) representa a função pai de todas as funções de valor absoluto. Isto significa que g(x) = |x|. Para encontrar a expressão para h(x), multiplicamos a expressão de g(x) por 3. Assim, temos h(x) = 3|x|.
Exemplo 7
P>P>Conte as transformações feitas em f(x) para atingir h(x).
- f(x) = x2 → h(x) = 3×2 + 24x + 48
- f(x) = √x → h(x) = 2√(x + 2)
- f(x) = ex → h(x) = 5(ex – 2) – 1
Solução
- Tentemos primeiro factorar a expressão para h(x) para ver se conseguimos encontrar as transformações aplicadas em f(x). Comece pelo factor h(x):
- h(x) = 3(x2 + 8x + 16) = 3(x + 4)2 = 3 ∙ f(x + 4)
- Desta forma factorizada, podemos ver que h(x) é o resultado quando f(x) é traduzido 4 unidades para a esquerda e esticado verticalmente por 3.
- Li>Nota do factor multiplicado por √x e a unidade subtraída do valor de entrada.
- Este resultado para h(x) = 2 ∙ f(x + 2).
- Hence, f(x) tem de ser traduzido 2 unidades para a esquerda e esticado verticalmente por 2.
- Li>Vamos observar a diferença entre ex e h(x).
- h(x) = 5 ∙ ex – 2 -1 , portanto, temos h(x) = 5 ∙ f(x – 2) – 1.
- Li>Isto significa que f(x) é traduzido 2 unidades para a direita, esticado verticalmente por 5, e traduzido uma unidade para baixo.
Exemplo 8
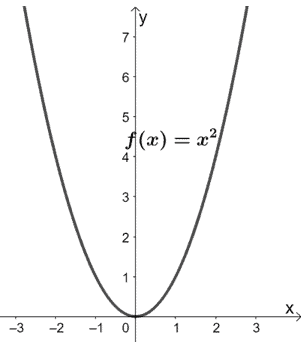
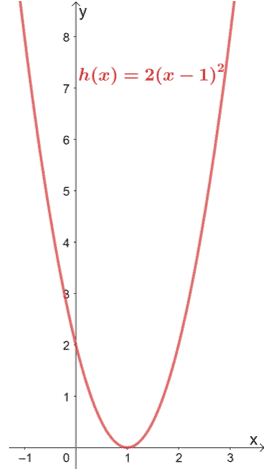
Quais são as transformações feitas em f(x) para que resultem em h(x) = 2×2 – 4x + 2? Use o gráfico de f(x) mostrado abaixo para o guiar. Aplique as transformações ao gráfico h(x).
Solução
P>Tentemos primeiro factorar a expressão para h(x) para ver se conseguimos encontrar as transformações aplicadas em f(x).
Begin, factorizando o factor comum partilhado pelos três termos.
2×2 – 4x + 2 = 2(x2 – 2x + 1)
Factor a expressão usando (a – b)2 = a2 – 2ab + b2.
2(x2 – 2x + 1) = 2(x – 1)2
Hence, temos h(x) = 2(x – 1)2. Desta forma, podemos ver o seguinte:
- De (x – 1)2, podemos ver que f(x) foi traduzido uma unidade para a direita.
- O gráfico resultante foi depois esticado verticalmente por um factor de 2,
Vamos utilizar estas transformações e o gráfico de f(x) para o gráfico h(x). Assim, comecemos por traduzir a função de f(x) y = x2 uma unidade para a direita.
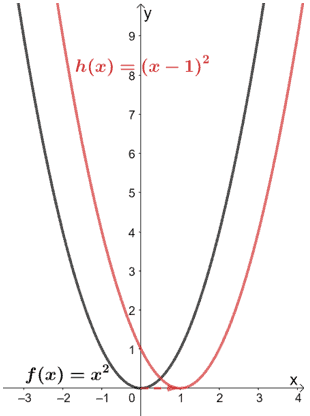
Agora, vamos esticar o gráfico verticalmente por um factor de escala de dois.
Vamos retirar a função de referência e devolver o gráfico final de h(x).
Este exemplo mostra como as transformações podem poupar tempo nas famílias de funções gráficas.
Perguntas Práticas
1. A função, g(x), é obtida por estiramento vertical f(x) = 3×3 + 2 por um factor de escala de 4. Qual das seguintes é a expressão correcta para g(x)?
a. g(x) = 3×3 + 8
b. g(x) = 3×3 + 6
c. g(x) = 12×3 + 2
d. g(x) = 12×3 + 8
2. A tabela de valores para f(x) é mostrada abaixo. Se g(x) = 3-f(x), construir uma tabela de valores para a função g(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -27 | -8 | -1 | 0 | 1 | 8 | 27 |
3. Preencha os espaços em branco para que as seguintes declarações sejam verdadeiras, dado que f(x) = √x.
a. Se g(x) = 5√x, a função g(x) é esticada verticalmente por um factor de escala de ________.
b. Se o gráfico de f(x) é esticado verticalmente por um factor de 4 para atingir h(x), então h(x) = ___ ∙ f(x).
c. Se o gráfico de f(x) for esticado verticalmente por um factor 2, a expressão para h(x) é ________.
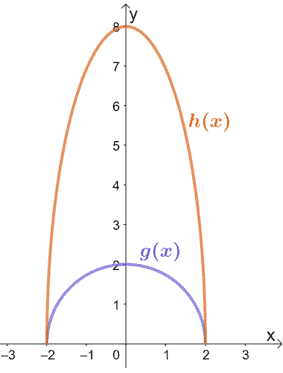
4. Observe as duas funções mostradas abaixo e relacione h(x) com g(x). Se g(x) = √(4 – x2), qual é a expressão para h(x)?
5. A função, A(x), modela a distância (em km) percorrida pelo carro A ao longo do tempo (em horas).
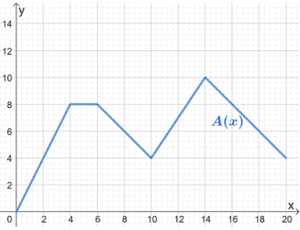
Mary quis comparar este modelo com B(x), cujo movimento segue o mesmo padrão, mas o carro observado pode cobrir três vezes a distância de A(x). Use o gráfico para A(x) para esboçar o gráfico de B(x).
6. Quais são as transformações feitas em f(x) para que resulte h(x) = 5x + 6? Use o facto de que f(x) é a função de pai de todas as funções lineares. Aplique as transformações no gráfico h(x).
7. Encontre as transformações feitas para cada par de funções e o gráfico h(x) para cada caso.
a. g(x) = x2 → h(x) = 5×2 – 20x + 20
b. g(x) = √x → h(x) = 3√(x – 1)
c. g(x) = 2x → h(x) = 3(2x – 2) + 6
p>Imagens/desenhos matemáticos são criados com GeoGebra.