Apresentamos uma visão microscópica da reacção química entre oxigénio e hidrogénio. A equação
\
representa o mesmo evento em termos de símbolos químicos e fórmulas.
Vimos também que as plantas formam glucose a partir de CO2 e H2O:
\
Mas como é que um químico praticante descobre o que está a ocorrer na escala microscópica? Quando uma reacção é observada pela primeira vez, pouco se sabe sobre a natureza microscópica dos produtos. É portanto necessário determinar experimentalmente a composição e fórmula de uma substância recém-sintetizada.
O primeiro passo de tal procedimento é normalmente separar e purificar os produtos de uma reacção. Os produtos acima são fáceis de separar, porque são líquidos ou sólidos, enquanto que os reagentes são gasosos. Mas como se pode determinar que a fórmula deve ser H2O, e não H2O2? E as plantas produzem misturas de hidratos de carbono durante a fotossíntese, que devem ser separadas por cromatografia ou outras técnicas antes de poderem ser identificadas. A glicose é talvez o açúcar simples mais comum, e existe em duas formas moleculares, com a fórmula química C6H12O6:
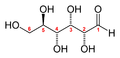
a forma de cadeia aberta de glicose
a forma cíclica da glucose
As plantas podem produzir outros açúcares simples com estruturas semelhantes, como D-ribulose (C5H10O5), D-frutose (C6H12O6) e di- ou polissacáridos (com dois ou mais açúcares simples ligados entre si) como a sacarose (C12H22O11) ou Maltose (C12H22O11).
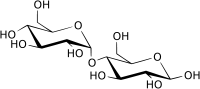
Como pode ser identificado o produto real?
Uma resposta envolve análise quantitativa – a determinação da percentagem por massa de cada elemento do composto. Tais dados são geralmente relatados como a composição percentual.
Exemplo \(\PageIndex{1}}): Composição percentual
Quando 10,0 g de oxigénio reage com hidrogénio suficiente, forma-se 11,26 g de um composto puro. Calcular a composição percentual a partir destes dados experimentais.
Solução
A percentagem de oxigénio é a massa de oxigénio dividida pela massa total do composto vezes 100%:
O resto do composto (11.26 g – 10 g = 1,26 g) é hidrogénio:
\
Como verificação, verificar se as percentagens aumentam para 100:
88,81% + 11.19% = 100%
Para obter a fórmula a partir de dados de composição percentual, temos de descobrir quantos átomos de hidrogénio existem por átomo de oxigénio. Numa escala macroscópica, isto corresponde à razão entre a quantidade de hidrogénio e a quantidade de oxigénio. Se a fórmula for H2O, não só indica que existem dois átomos de hidrogénio por átomo de oxigénio, como também diz que existem 2 mol de átomos de hidrogénio para cada 1 mol de átomos de oxigénio. Ou seja, a quantidade de hidrogénio é o dobro da quantidade de oxigénio. Os números na relação entre a quantidade de bromo e a quantidade de mercúrio (2:1) são os subscritos de hidrogénio e oxigénio na fórmula.
Exemplo \i>(PageIndex{2}}): Determinação da fórmula
Determinar a fórmula do composto cuja composição percentual foi calculada no exemplo anterior.
Solução
Para conveniência, assumir que temos 100 g do composto. Destes, 88,81 g (88,81%) é oxigénio e 11,19 g é hidrogénio. Cada massa pode ser convertida para uma quantidade de substância
\begin{align} & n_texto{\i}=texto{88}=texto{.81 g}times {\i}frac{\i}{\i1 mol O}{\i1 mol O}{\i1}text{.16}text{.00 g}=texto{.550 mol O} \\&
n_texto{H}=texto{11}text{.19 g}times {1 mol H}{1 mol H}{1 mol H}text{.008 g}=texto{.101 mol H}=texto{.101 mol H \\ {alinhamento}
Por isso a fórmula é H11.101O5.550, mas sabemos que não existem fracções de átomos, por isso temos de colocar isto de uma forma padrão. Para tal, dividimos a maior quantidade pela menor:
\
Para a fórmula é H1.998O1, mas novamente, parece haver um problema. A razão 1,998 mol H para 1 mol O também implica que há 1,998 átomos de H por 1 O átomo. Se a teoria atómica estiver correcta, não existe tal coisa como 0,998 átomo; mas lembrando que as nossas medições são apenas boas para três números significativos, arredondamos 1,998 para 2,00 e escrevemos a fórmula como H2O.
Exemplo {3}(PageIndex{3}}): Formula of Compound
Um óxido de hidrogénio tem a composição 94,07% O e 5,93% H. Encontre a sua fórmula.
Solução
Ganho assumir uma amostra de 100-g e calcular a quantidade de cada elemento:
\begin{align} & n_texto{\i}=texto{\i}=texto{\i}{.07 g}times {\i}frac{\i}{\i1 mol O}{\i1 mol O}text{.00 g}=texto{.88 mol O \\&
n_texto{H}=texto{5}text{.93 g}times |frac{1 mol H}{1 mol H}{1 mol H}}text{.008 g}=texto{.5}text{.88 mol H} \\ {align}
A razão é
Por isso a fórmula é H5.88O5.88, que é uma razão de 1:1 dentro da precisão experimental. Assim, atribuiríamos a fórmula HO.
A fórmula obtida no Exemplo 3 não corresponde a nenhum dos dois óxidos de hidrogénio que já discutimos. Trata-se de um terceiro? A resposta é não porque o nosso método só pode determinar o rácio de H para O. O rácio 1:1 é o mesmo que 2:2, pelo que o nosso método dará o mesmo resultado para HO ou H2O2 (ou H7O7, se é que existe). A fórmula determinada por este método é chamada a fórmula empírica ou fórmula mais simples. Ocasionalmente, como no caso do peróxido de hidrogénio, a fórmula empírica difere da composição molecular real, ou da fórmula molecular. A determinação experimental do peso molecular para além da composição percentual permite o cálculo da fórmula molecular.
Exemplo \(\PageIndex{4}}): Fórmulas Empíricas e Moleculares
Um composto cujo peso molecular é 28 contém 85,6% C e 14,4% H. Determina as suas fórmulas empíricas e moleculares.
Solução
\begin{align} & n_texto{{C}}=texto{85}=texto{.6 g}times |frac{1 mol C}{1 mol C}{12 mol C}=texto{.01 g}=texto{.7 mol C}=texto{.13 mol C \\&
n_texto{H}=texto{14}text{.4 g}times |frac{1 mol H}{1 mol H}{1 mol H}}text{.008 g}=texto{14}text{.3 mol H} \\ {alinhamento}
Então a fórmula é C7.13H14.3, mas para obter subscritos integrais dividimos cada um pelos mais pequenos: \
A fórmula empírica é portanto CH2. O peso molecular correspondente à fórmula empírica é
12.01 + 2 × 1.008 = 14.03
Desde que o peso molecular experimental é o dobro, todos os subscritos devem ser duplicados e a fórmula molecular é C2H4.
Exemplo \(\PageIndex{5}}): Empirical Formula
D-Xylose contém 40,0% C, 6,71% H, e 53,29% O. Qual é a sua fórmula empírica?
Solução
\begin{align} & n_texto{H}=texto{6}=texto{.71 g}times |frac{1 mol H}}{1 mol H}{1 mol H}}text{.008 g}=texto{.66 mol H} \\&
n_texto{{C}=texto{40}text{.00 g}times {.00 mol C}{1 mol C}{12 mol C}{.01 g}=texto{.3 mol C}=texto{.33 mol C \\&
n_texto{\i}=texto{53}=texto{.29 g}times {\i1 mol O}{\i1 mol O}{\i1}textos{.00 g}=texto{.33 mol O} \\ {alinhamento}
Então a fórmula é C3.33H6.66O3.33, e dividindo os três pela menor quantidade de substância obtemos CH2O.
begin{alinhamento} & {n_text{C}}{n_text{O}=frac{3 mol C}{.33 mol C}{texto{3}{.33 mol O}=frac{1 mol H \\&frac{n_text{H}}{n_text{O}=frac{4 mol H}{.44 mol H}{texto{.22 mol O}=frac{2}text{.00 mol H}{.1 mol O}} \\ {align}
Agora vemos onde os hidratos de carbono obtêm o seu nome. Todos eles têm fórmulas como Cn(H2O)m, pelo que todos se parecem com hidratos (compostos contendo água) de carbono. D-Xilose é na realidade C5(H2O)5 ou C5H10O5, Glucose é C6(H12O)6 ou C6H12O6, e Sacarose é C12(H2O)11 ou C12H22O11.
Vimos que o erro experimental pode dar rácios molares que não são unidades exactas. Ocasionalmente a razão de quantidades está mais longe de um número inteiro do que pode ser explicado por erro experimental, como no exemplo seguinte.
Exemplo \\i(\iIndex{6}}): Fórmula Empírica da Aspirina
Aspirina contém 60,0% C, 4,48% H, e 35,5% O. Qual é a sua fórmula empírica?
Solução
\begin{align} & n_texto{H}=texto{14}=texto{.4 g}times |frac{1 mol H}}{1 mol H}{1 mol H}}text{.008 g}=texto{.14}text{.3 mol H} \\&
n_texto{C}=texto{85}=texto{.6 g}times |frac{1 mol C}{1 mol C}{12 mol C}=texto{.01 g}=texto{.7 mol C}=texto{.13 mol C \\&
n_texto{O}=texto{35}text{.5 g}text{.5 g}times |frac{1 mol O}{1 mol O}text{16}text{.00 g}=texto{.22 mol O} \\ Dividir os três pela menor quantidade de substância
begin{align} & {n_text{C}}{n_text{O}=frac{5 mol C}{.00 mol C}{texto{.22 mol O}=frac{2 mol O}=text{.25 mol H}{.25 mol H}{1 mol O}} \\&frac{n_text{H}}{n_text{O}=frac{4 mol H}{.44 mol H}{texto{.22 mol O}=frac{2}text{.00 mol H}{.1 mol O}} \\ P>Até ao fim, existem claramente duas vezes mais átomos H do que átomos O, mas a proporção de C para O não é tão óbvia. Temos de converter 2,25 para uma razão de pequenos números inteiros. Isto pode ser feito através da alteração dos números após o ponto decimal para uma fracção. Neste caso, .25 passa a ¼. Assim, 2,25 = 2¼ = 9/4, e
\
Também podemos escrever
\
Assim a fórmula empírica é C9H8O4.
Após alguém ter determinado uma fórmula -empírica ou molecular – é possível que outra pessoa faça o cálculo inverso. Encontrar a composição por percentagem de peso a partir da fórmula revela-se frequentemente bastante informativo, como mostra o exemplo seguinte.
Exemplo \i>(\i>PageIndex{7}}): Composição percentual de um Açúcar
Como vimos acima, todos os hidratos de carbono têm a fórmula geral Cn(H2O)m. Todos os açúcares simples têm a fórmula geral Cn(H2O)n, pelo que todos têm a mesma percentagem de C, H, e O.
a. Calcular a percentagem de C na glucose. b. Mostrar que o composto C8(H2O)4 não pode ser um açúcar simples calculando a sua composição percentual.
Solução
a. C6(H2O)6 contém 6 mol C, 12 mol H, e 6 mol O. A massa molar é assim
p>M = (6 x 12,011) + (12 x 1,008) + (6 x 16) = 180 g mol-1
A amostra de 1-mol pesaria 180,56 g. A massa de 6 mol C que contém é
\\\\\\\\i>Por isso a percentagem de C é
\i>/p>As percentagens de H e O são facilmente calculadas como
\i>begin{align} & m_text{H}}=text{12 mol H}cdot=frac{1.008 g}{1 mol H}=text{12.096 g}&text{%H}= {12.008 g}=frac{12.096 g}=text{12.096 g}}&
text{%H}= {12.096 g}}div096 g}{{180.56 g}{100%}=texto{6.70%}& m_{texto{O}=texto{6 mol O}cdot=frac{16.00 g}{1 mol O}{1 mol O}=text{96.00 g}& {%O}= }frac{96.00 g}{180.56 g}}cdot=text{100%}=text{53.17%}{alinhamentoEmbora não seja estritamente necessário para responder ao problema, as duas últimas percentagens fornecem uma verificação dos resultados. O total 40,00 + 6,70% + 53,17% = 100,00% como deveria.
Nota que para qualquer açúcar simples,
independentemente de quantos carbonos contém (açúcares simples são trioses, C3H6O3, tetroses, C4H8O4, pentoses, e hexoses. O mesmo vale para a percentagem H e O.
b. A massa molar de C8(H2O)4 é de 168,15;
%C = x 100% = 57,14%, não a característica de 40% de açúcares simples.
Similarmente,
%H = x 100% = 4,80% e a percentagem O é 38,06%.
From ChemPRIME: 2.11: Formulas e Composição