Investigação experimental, muitas vezes considerada como o “padrão de ouro” nos desenhos de investigação, é um dos mais rigorosos de todos os desenhos de investigação. Neste desenho, uma ou mais variáveis independentes são manipuladas pelo investigador (como tratamentos), os sujeitos são atribuídos aleatoriamente a diferentes níveis de tratamento (atribuição aleatória), e os resultados dos tratamentos sobre os resultados (variáveis dependentes) são observados. A força única da investigação experimental é a sua validade interna (causalidade) devido à sua capacidade de ligar causa e efeito através da manipulação do tratamento, ao mesmo tempo que controla para o efeito espúrio da variável externa.
A investigação experimental é mais adequada para a investigação explicativa (e não para a investigação descritiva ou exploratória), onde o objectivo do estudo é examinar as relações causa-efeito. Também funciona bem para a investigação que envolve um conjunto relativamente limitado e bem definido de variáveis independentes que podem ou ser manipuladas ou controladas. A investigação experimental pode ser realizada em laboratório ou em campo. As experiências laboratoriais, realizadas em cenários de laboratório (artificiais), tendem a ser de elevada validade interna, mas isto tem um custo de baixa validade externa (generalizabilidade), porque o cenário artificial (de laboratório) em que o estudo é realizado pode não reflectir o mundo real. As experiências de campo, realizadas em cenários de campo como numa organização real, e elevadas tanto em validade interna como externa. Mas tais experiências são relativamente raras, devido às dificuldades associadas à manipulação de tratamentos e ao controlo de efeitos estranhos num ambiente de campo.
A investigação experimental pode ser agrupada em duas grandes categorias: desenhos experimentais verdadeiros e desenhos quase-experimentais. Ambos os desenhos requerem manipulação de tratamento, mas embora as verdadeiras experiências também exijam uma atribuição aleatória, as quase-experimentações não requerem. Por vezes, também nos referimos à investigação não experimental, que não é realmente um desenho de investigação, mas um termo que inclui todos os tipos de investigação que não empregam manipulação de tratamento ou atribuição aleatória, tais como investigação de inquéritos, investigação observacional, e estudos correlacionais.
Conceitos Básicos
Grupos de tratamento e controlo. Na investigação experimental, alguns sujeitos são administrados a um ou mais sujeitos um estímulo experimental chamado tratamento (o grupo de tratamento ), enquanto outros sujeitos não recebem tal estímulo (o grupo de controlo ). O tratamento pode ser considerado bem sucedido se os sujeitos do grupo de tratamento avaliarem mais favoravelmente as variáveis de resultados do que os sujeitos do grupo de controlo. Podem ser administrados vários níveis de estímulo experimental, caso em que pode haver mais do que um grupo de tratamento. Por exemplo, a fim de testar os efeitos de um novo medicamento destinado a tratar uma determinada condição médica como a demência, se uma amostra de pacientes com demência for dividida aleatoriamente em três grupos, com o primeiro grupo a receber uma dose elevada do medicamento, o segundo grupo a receber uma dose baixa, e o terceiro grupo a receber um placebo como um comprimido de açúcar (grupo de controlo), então os dois primeiros grupos são grupos experimentais e o terceiro grupo é um grupo de controlo. Após administrar o fármaco durante um período de tempo, se a condição dos sujeitos do grupo experimental melhorou significativamente mais do que os sujeitos do grupo de controlo, podemos dizer que o fármaco é eficaz. Podemos também comparar as condições dos grupos experimentais de dose alta e baixa para determinar se a dose alta é mais eficaz do que a dose baixa.
Manipulação do tratamento. Os tratamentos são a característica única da investigação experimental que distingue este desenho de todos os outros métodos de investigação. A manipulação de tratamento ajuda a controlar a “causa” nas relações causa-efeito. Naturalmente, a validade da investigação experimental depende de quão bem o tratamento foi manipulado. A manipulação do tratamento deve ser verificada usando pré-testes e testes-piloto antes do estudo experimental. Quaisquer medições realizadas antes da administração do tratamento são chamadas medidas de pré-teste, enquanto que as realizadas após o tratamento são medidas de pós-teste .
Selecção e atribuição aleatória. A selecção aleatória é o processo de retirar aleatoriamente uma amostra de uma população ou de uma moldura de amostragem. Esta abordagem é tipicamente empregada na pesquisa de inquérito, e assegura que cada unidade da população tem uma hipótese positiva de ser seleccionada para a amostra. A atribuição aleatória é, contudo, um processo de atribuição aleatória de indivíduos a grupos experimentais ou de controlo. Esta é uma prática padrão na verdadeira investigação experimental para assegurar que os grupos de tratamento são semelhantes (equivalentes) uns aos outros e ao grupo de controlo, antes da administração do tratamento. A selecção aleatória está relacionada com a amostragem, e está, portanto, mais estreitamente relacionada com a validade externa (generalizabilidade) dos resultados. No entanto, a selecção aleatória está relacionada com a concepção, e está, portanto, mais relacionada com a validade interna. É possível ter selecção aleatória e atribuição aleatória em investigação experimental bem concebida, mas a investigação quase-experimental não envolve selecção aleatória nem atribuição aleatória.
Ameaças à validade interna. Embora os desenhos experimentais sejam considerados mais rigorosos do que outros métodos de investigação em termos da validade interna das suas inferências (em virtude da sua capacidade de controlar as causas através da manipulação do tratamento), não são imunes às ameaças de validade interna. Algumas destas ameaças à validade interna são descritas abaixo, no contexto de um estudo do impacto de um programa especial de reforço da matemática para melhorar as capacidades matemáticas dos alunos do ensino secundário.
- li>Ameaça histórica é a possibilidade de que os efeitos observados (variáveis dependentes) sejam causados por eventos estranhos ou históricos e não pelo tratamento experimental. Por exemplo, a melhoria da classificação matemática pós-remedial dos alunos pode ter sido causada pela sua preparação para um exame de matemática na sua escola, em vez do programa de matemática correctivo.
- Ameaça de maturação refere-se à possibilidade de que os efeitos observados sejam causados pela maturação natural dos sujeitos (por exemplo uma melhoria geral na sua capacidade intelectual de compreender conceitos complexos) em vez do tratamento experimental.
- Ameaça de teste é uma ameaça nos desenhos pré-pós em que as respostas pós-teste dos sujeitos são condicionadas pelas suas respostas pré-teste. Por exemplo, se os alunos se lembrarem das suas respostas da avaliação pré-teste, podem tender a repeti-las no exame pós-teste. Não realizar um pré-teste pode ajudar a evitar esta ameaça.
- li>Ameaça de instrumentação , que também ocorre nos desenhos pré-pós, refere-se à possibilidade de a diferença entre as pontuações do pré-teste e do pós-teste não se dever ao programa de matemática correctivo, mas sim a alterações no teste administrado, tais como o pós-teste ter um grau de dificuldade superior ou inferior ao do pré-teste.
- li>Ameaça à mortalidade refere-se à possibilidade de os sujeitos poderem estar a abandonar o estudo a taxas diferenciais entre os grupos de tratamento e de controlo devido a uma razão sistemática, de tal modo que as desistências foram na sua maioria estudantes que obtiveram notas baixas no teste de pré-teste. Se os alunos com baixo desempenho desistirem, os resultados do pós-teste serão artificialmente inflacionados pela preponderância de alunos com alto desempenho.
- li>Ameaça de regressão, também chamada regressão à média, refere-se à tendência estatística do desempenho global de um grupo numa medida durante um pós-teste para regredir para a média dessa medida e não na direcção prevista. Por exemplo, se os sujeitos pontuaram alto num pré-teste, terão tendência a pontuar mais baixo no pós-teste (mais próximo da média) porque as suas pontuações altas (longe da média) durante o pré-teste foi possivelmente uma aberração estatística. Este problema tende a ser mais prevalente em amostras não aleatórias e quando as duas medidas são imperfeitamente correlacionadas.
Designs Experimentais de dois grupos
Os desenhos experimentais verdadeiros mais simples são dois desenhos de grupo envolvendo um grupo de tratamento e um grupo de controlo, e são ideais para testar os efeitos de uma única variável independente que pode ser manipulada como tratamento. Os dois desenhos básicos de dois grupos são o desenho do grupo de controlo de pré-testes e o desenho do grupo de controlo só de pós-testes, enquanto que as variações podem incluir desenhos de covariância. Estes desenhos são frequentemente representados utilizando uma notação de desenho padronizada, onde R representa a atribuição aleatória de sujeitos a grupos, X representa o tratamento administrado ao grupo de tratamento, e O representa as observações de pré-teste ou pós-teste da variável dependente (com diferentes subscritos para distinguir entre observações de pré-teste e pós-teste dos grupos de tratamento e controlo).
Desenho do grupo de controlo de pré-teste-pós-teste. Neste desenho, os sujeitos são aleatoriamente atribuídos a grupos de tratamento e controlo, sujeitos a uma medição inicial (pré-teste) das variáveis dependentes de interesse, o grupo de tratamento é administrado um tratamento (representando a variável independente de interesse), e as variáveis dependentes são novamente medidas (pós-teste). A notação deste desenho é mostrada na Figura 10.1.
Figure 10.1. O efeito E do tratamento experimental no desenho do pré-teste pós-teste é medido como a diferença nas pontuações pós-teste e pré-teste entre os grupos de tratamento e controlo:
p>E = (O 2 – O 1 ) – (O 4 – O 3 )
Análise estatística deste desenho envolve uma análise simples de variância (ANOVA) entre os grupos de tratamento e controlo. O desenho pós-teste trata várias ameaças à validade interna, tais como maturação, testes, e regressão, uma vez que se pode esperar que estas ameaças influenciem tanto os grupos de tratamento como os grupos de controlo de forma semelhante (aleatória). A ameaça de selecção é controlada através de atribuição aleatória. No entanto, podem existir ameaças adicionais à validade interna. Por exemplo, a mortalidade pode ser um problema se houver taxas diferenciais de abandono entre os dois grupos, e a medição do pré-teste pode influenciar a medição pós-teste (especialmente se o pré-teste introduzir tópicos ou conteúdos invulgares).
Concepção do grupo de controlo apenas de pós-teste . Este desenho é uma versão mais simples do desenho do pré-teste-pós-teste onde as medições do pré-teste são omitidas. A notação de desenho é mostrada na Figura 10.2.
Figure 10.2. O efeito do tratamento é medido simplesmente como a diferença na pontuação pós-teste entre os dois grupos:
p>E = (O 1 – O 2 )
p> A análise estatística apropriada deste desenho é também uma análise de variância de dois grupos (ANOVA). A simplicidade deste desenho torna-o mais atractivo do que o desenho de pré-teste-pós-teste em termos de validade interna. Este desenho controla a maturação, testes, regressão, selecção e interacção pré-teste-pós-teste, embora a ameaça de mortalidade possa continuar a existir.
Designs de co-variação . Por vezes, as medidas das variáveis dependentes podem ser influenciadas por variáveis estranhas chamadas covariantes . As covariantes são aquelas variáveis que não são de interesse central para um estudo experimental, mas devem, no entanto, ser controladas num desenho experimental, a fim de eliminar o seu efeito potencial sobre a variável dependente e, portanto, permitir uma detecção mais precisa dos efeitos das variáveis independentes de interesse. Os desenhos experimentais discutidos anteriormente não controlavam para tais covariates. Um desenho de covariância (também chamado desenho de variável concomitante) é um tipo especial de desenho de grupo de controlo pós-teste em que a medida de pré-teste é essencialmente uma medida dos covariates de interesse e não a das variáveis dependentes. A notação de desenho é mostrada na Figura 10.3, onde C representa os covariáveis:
Figure 10.3. Desenho de covariância
Porque a medida de pré-teste não é uma medida da variável dependente, mas sim uma covariância, o efeito do tratamento é medido como a diferença nas pontuações pós-teste entre os grupos de tratamento e controlo como:
E = (O 1 – O 2 )
P>Due à presença de covariantes, a análise estatística correcta deste desenho é uma análise de covariância em dois grupos (ANCOVA). Este desenho tem todas as vantagens de um desenho apenas pós-teste, mas com validade interna devido ao controlo de covariates. Os desenhos de covariância também podem ser alargados ao desenho do grupo de controlo de pré-testes. 
Designs de grupo de controlo
Designs de dois grupos são inadequados se a sua investigação exigir a manipulação de duas ou mais variáveis independentes (tratamentos). Nesses casos, seriam necessários quatro ou mais desenhos de grupo. Tais desenhos, bastante populares na investigação experimental, são vulgarmente chamados de desenhos factoriais. Cada variável independente neste desenho é chamada um factor , e cada subdivisão de um factor é chamada um nível . Os desenhos factoriais permitem ao investigador examinar não só o efeito individual de cada tratamento sobre as variáveis dependentes (chamados efeitos principais), mas também o seu efeito conjunto (chamados efeitos de interacção).
O desenho factorial mais básico é um desenho factorial 2 x 2, que consiste em dois tratamentos, cada um com dois níveis (tais como alto/baixo ou presente/ausente). Por exemplo, digamos que se pretende comparar os resultados de aprendizagem de dois tipos diferentes de técnicas de instrução (em sala de aula e em linha), e também se pretende examinar se estes efeitos variam com o tempo de instrução (1,5 ou 3 horas por semana). Neste caso, tem dois factores: tipo de instrução e tempo de instrução; cada um com dois níveis (em aula e em linha para o tipo de instrução, e 1,5 e 3 horas/semana para o tempo de instrução), como se mostra na Figura 8.1. Se desejar acrescentar um terceiro nível de tempo instrucional (digamos 6 horas/semana), então o segundo factor será constituído por três níveis e terá um desenho factorial de 2 x 3. Por outro lado, se desejar adicionar um terceiro factor, tal como trabalho de grupo (presente versus ausente), terá um desenho factorial de 2 x 2 x 2. Nesta notação, cada número representa um factor, e o valor de cada factor representa o número de níveis nesse factor.
Figure 10.4. 2 x 2 desenho factorial
Designs factoriais também podem ser representados usando uma notação de desenho, tal como a apresentada no painel direito da Figura 10.4. R representa a atribuição aleatória de sujeitos a grupos de tratamento, X representa os próprios grupos de tratamento (os subscritos de X representam o nível de cada factor), e O representa as observações da variável dependente. Note-se que o desenho factorial 2 x 2 terá quatro grupos de tratamento, correspondentes às quatro combinações dos dois níveis de cada factor. Correspondentemente, o desenho 2 x 3 terá seis grupos de tratamento, e o desenho 2 x 2 x 2 terá oito grupos de tratamento. Como regra geral, cada célula de um desenho factorial deverá ter um tamanho mínimo de amostra de 20 (esta estimativa deriva dos cálculos de potência de Cohen baseados em tamanhos de efeito médios). Assim, um desenho factorial 2 x 2 x 2 requer um tamanho mínimo total de amostra de 160 indivíduos, com pelo menos 20 indivíduos em cada célula. Como se pode ver, o custo da recolha de dados pode aumentar substancialmente com mais níveis ou factores no seu desenho factorial. Por vezes, devido a restrições de recursos, algumas células em tais desenhos factoriais podem não receber qualquer tratamento, que são chamados desenhos factoriais incompletos . Tais desenhos incompletos prejudicam a nossa capacidade de extrair inferências sobre os factores incompletos.
Num desenho factorial, diz-se que existe um efeito principal se a variável dependente mostrar uma diferença significativa entre vários níveis de um factor, em todos os níveis de outros factores. Nenhuma alteração na variável dependente entre níveis de factores é o caso nulo (linha de base), a partir do qual os efeitos principais são avaliados. No exemplo acima, pode-se ver um efeito principal de tipo instrucional, tempo instrucional, ou ambos nos resultados da aprendizagem. Existe um efeito de interacção quando o efeito das diferenças de um factor depende do nível de um segundo factor. No nosso exemplo, se o efeito do tipo instrucional sobre os resultados da aprendizagem for maior durante 3 horas/semana de tempo instrucional do que durante 1,5 horas/semana, então podemos dizer que existe um efeito de interacção entre o tipo instrucional e o tempo instrucional sobre os resultados da aprendizagem. Note-se que a presença de efeitos de interacção domina e torna os efeitos principais irrelevantes, e não é significativo interpretar os efeitos principais se os efeitos de interacção forem significativos.
Designs Experimentais Híbridos
Designs Híbridos são aqueles que são formados pela combinação de características de desenhos mais estabelecidos. Três desses desenhos híbridos são desenhos de blocos aleatórios, desenho de quatro grupos Solomon, e desenho de réplicas alternadas.
Desenho de blocos aleatórios. Esta é uma variação do desenho do grupo de controlo pós-teste ou pré-teste, onde a população de sujeitos pode ser agrupada em subgrupos relativamente homogéneos (chamados blocos) dentro dos quais a experiência é replicada. Por exemplo, se se pretender replicar o mesmo desenho pós-teste apenas entre estudantes universitários e profissionais a tempo inteiro (dois blocos homogéneos), os sujeitos em ambos os blocos são divididos aleatoriamente entre grupo de tratamento (recebendo o mesmo tratamento) ou grupo de controlo (ver Figura 10.5). O objectivo desta concepção é reduzir o “ruído” ou variação nos dados que podem ser atribuíveis a diferenças entre os blocos, para que o efeito real de interesse possa ser detectado com maior precisão.
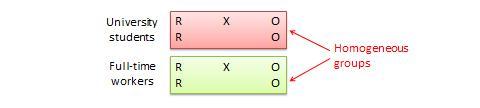
Figure 10.5. Desenho de blocos aleatórios.
Solomon four-group design . Neste desenho, a amostra é dividida em dois grupos de tratamento e dois grupos de controlo. Um grupo de tratamento e um grupo de controlo recebem o pré-teste, e os outros dois grupos não. Este desenho representa uma combinação de desenho de grupo de controlo pós-teste apenas e pré-teste-pós-teste, e destina-se a testar o potencial efeito enviesante da medição pré-teste sobre as medidas pós-teste que tendem a ocorrer nos desenhos pré-teste-pós-teste, mas não nos desenhos pós-teste apenas. A notação de desenho é mostrada na Figura 10.6.
Figure 10.6. Desenho de quatro grupos de Salomão
Desenho de replicação comutada . Este é um desenho de dois grupos implementado em duas fases com três ondas de medição. O grupo de tratamento na primeira fase serve como o grupo de controlo na segunda fase, e o grupo de controlo na primeira fase torna-se o grupo de tratamento na segunda fase, como ilustrado na Figura 10.7. Por outras palavras, o desenho original é repetido ou replicado temporariamente com as funções de tratamento/controlo alternadas entre os dois grupos. No final do estudo, todos os participantes terão recebido o tratamento durante a primeira ou a segunda fase. Esta concepção é mais viável em contextos organizacionais onde os programas organizacionais (por exemplo, formação de funcionários) são implementados de forma faseada ou são repetidos a intervalos regulares.
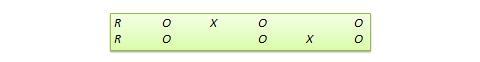
Figure 10.7. Desenho de replicação comutado.
Designs de quase-experimental
Designs de quase-experimental são quase idênticos aos verdadeiros desenhos experimentais, mas sem um ingrediente chave: atribuição aleatória. Por exemplo, uma secção inteira da classe ou uma organização é utilizada como grupo de tratamento, enquanto outra secção da mesma classe ou uma organização diferente na mesma indústria é utilizada como grupo de controlo. Esta falta de atribuição aleatória resulta potencialmente em grupos não equivalentes, tais como um grupo que possui maior domínio de um determinado conteúdo do que o outro grupo, digamos em virtude de ter um melhor professor num semestre anterior, o que introduz a possibilidade de enviesamento de selecção. Os desenhos quase-experimentais são portanto inferiores aos verdadeiros desenhos experimentais em intervalos de validade devido à presença de uma variedade de ameaças relacionadas com a selecção, tais como a ameaça de selecção-maturação (os grupos de tratamento e controlo que amadurecem a ritmos diferentes), a ameaça de selecção-história (sendo os grupos de tratamento e controlo diferentes o impacto por eventos estranhos ou históricos), ameaça de selecção-regressão (os grupos de tratamento e controlo regredindo para a média entre o pré-teste e o pós-teste a taxas diferentes), ameaça de selecção-instrumentação (os grupos de tratamento e controlo que respondem de forma diferente à medição), selecção-teste (os grupos de tratamento e controlo que respondem de forma diferente ao pré-teste), e selecção-mortalidade (os grupos de tratamento e controlo que demonstram taxas de desistência diferenciais). Dadas estas ameaças de selecção, é geralmente preferível evitar ao máximo os desenhos quase-experimentais.
Muitos verdadeiros desenhos experimentais podem ser convertidos em desenhos quase-experimentais, omitindo a atribuição aleatória. Por exemplo, a versão quasi-equivalente do desenho do grupo de controlo pré-teste-pós-teste é chamada desenho de grupos não equivalentes (NEGD), como mostrado na Figura 10.8, com atribuição aleatória R substituída por atribuição não equivalente (não aleatória) N . Da mesma forma, a versão quase-experimental do desenho de replicação comutada é chamada desenho de replicação comutada não equivalente (ver Figura 10.9).
Figure 10.8. NEGD design.
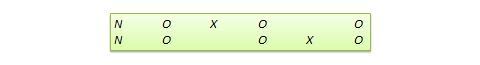p>Figure 10.9. Desenho de replicação alternada não equivalente. Além disso, existem bastantes desenhos não equivalentes únicos sem os correspondentes primos de desenho experimental verdadeiro. Alguns dos desenhos mais úteis são discutidos a seguir.
Desenho de regressão-descontinuidade (RD) . Este é um desenho não-equivalente de pré-teste-pós-teste em que os sujeitos são designados para tratamento ou grupo de controlo com base numa pontuação de corte numa medida de pré-programa. Por exemplo, os doentes graves podem ser atribuídos a um grupo de tratamento para testar a eficácia de um novo medicamento ou protocolo de tratamento e os doentes ligeiros são atribuídos ao grupo de controlo. Num outro exemplo, os estudantes que estão atrasados nos resultados de testes padronizados podem ser seleccionados para um programa curricular de remediação destinado a melhorar o seu desempenho, enquanto que aqueles que obtiveram uma pontuação elevada em tais testes não são seleccionados a partir do programa de remediação. A notação de desenho pode ser representada da seguinte forma, onde C representa a pontuação de corte:
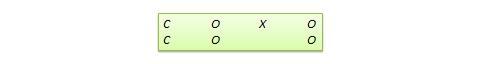
Figure 10.10. RD design.
Por causa da utilização de uma pontuação de corte, é possível que os resultados observados possam ser uma função da pontuação de corte e não do tratamento, o que introduz uma nova ameaça à validade interna. Contudo, a utilização da pontuação de corte também assegura que recursos limitados ou dispendiosos sejam distribuídos às pessoas que deles mais necessitam em vez de aleatoriamente por uma população, ao mesmo tempo que permite um tratamento quase-experimental. As pontuações dos grupos de controlo no desenho do RD não servem de referência para comparar as pontuações dos grupos de tratamento, dada a não equivalência sistemática entre os dois grupos. Pelo contrário, se não houver descontinuidade entre as pontuações de pré-teste e pós-teste no grupo de controlo, mas tal descontinuidade persistir no grupo de tratamento, então esta descontinuidade é vista como prova do efeito do tratamento.
Concepção de pré-teste proxy . Este desenho, mostrado na Figura 10.11, parece muito semelhante ao desenho padrão do NEGD (pré-teste-pós-teste), com uma diferença crítica: a pontuação do pré-teste é recolhida após a administração do tratamento. Uma aplicação típica deste desenho é quando um investigador é trazido para testar a eficácia de um programa (por exemplo, um programa educativo) depois de o programa já ter começado e os dados do pré-teste não estarem disponíveis. Em tais circunstâncias, a melhor opção para o investigador é muitas vezes utilizar uma medida pré-gravada diferente, tal como a média de pontos de notas dos estudantes antes do início do programa, como um substituto para os dados de pré-teste. Uma variação do desenho do pré-teste proxy é utilizar a recolha de dados pós-teste dos indivíduos, que podem estar sujeitos a um enviesamento de recolha, mas que, no entanto, podem fornecer uma medida de ganho ou alteração percebida na variável dependente.
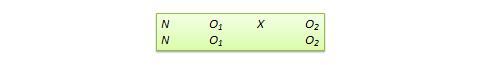
Figure 10.11. Desenho de pré-teste de protótipo.
Desenho separado de amostras de pré-teste-pós-teste . Este desenho é útil se não for possível recolher dados de pré-testes e pós-testes dos mesmos sujeitos por alguma razão. Como mostrado na Figura 10.12, existem quatro grupos neste desenho, mas dois grupos provêm de um único grupo não equivalente, enquanto os outros dois grupos provêm de um grupo não equivalente diferente. Por exemplo, pretende-se testar a satisfação do cliente com um novo serviço online que é implementado numa cidade mas não noutra. Neste caso, os clientes da primeira cidade servem como grupo de tratamento e os da segunda cidade constituem o grupo de controlo. Se não for possível obter medidas de pré-teste e pós-teste dos mesmos clientes, é possível medir a satisfação do cliente num determinado momento, implementar o novo programa de serviço, e medir a satisfação do cliente (com um conjunto diferente de clientes) depois de o programa ser implementado. A satisfação do cliente também é medida no grupo de controlo ao mesmo tempo que no grupo de tratamento, mas sem a implementação do novo programa. A concepção não é particularmente forte, porque não se pode examinar as alterações no grau de satisfação de qualquer cliente específico antes e depois da implementação, mas só se pode examinar o grau médio de satisfação do cliente. Apesar da menor validade interna, este desenho pode ainda ser uma forma útil de recolher dados quase-experimentais quando os dados de pré-teste e pós-teste não estão disponíveis nos mesmos sujeitos.
Figure 10.12. Desenho separado de amostras de pré-teste-pós-teste.
Desenho de variável dependente não equivalente (NEDV) . Este é um desenho pré-pós-pós-experimental de grupo único com duas medidas de resultado, em que se espera teoricamente que uma medida seja influenciada pelo tratamento e a outra medida não. Por exemplo, se estiver a conceber um novo currículo de cálculo para estudantes do ensino secundário, é provável que este currículo influencie as pontuações de cálculo pós-teste dos estudantes, mas não as pontuações de álgebra. No entanto, as pontuações de álgebra pós-teste podem ainda variar devido a factores alheios, tais como história ou maturação. Assim, as pontuações da álgebra pré-pós podem ser usadas como medida de controlo, enquanto que a do cálculo pré-pós pode ser tratada como a medida de tratamento. A notação de desenho, mostrada na Figura 10.13, indica o grupo único por um único N , seguido pelo pré-teste O 1 e o pós-teste O 2 para cálculo e álgebra para o mesmo grupo de estudantes. Este desenho é fraco em validade interna, mas a sua vantagem reside em não ter de utilizar um grupo de controlo separado.
Uma variação interessante do desenho NEDV é um desenho padrão que combina o desenho NEDV , que emprega múltiplas variáveis de resultados e uma teoria que explica o quanto cada variável será afectada pelo tratamento. O investigador pode então examinar se a previsão teórica é correspondida em observações reais. Esta técnica de correspondência de padrões, baseada no grau de correspondência entre padrões teóricos e observados, é uma forma poderosa de aliviar as preocupações de validade interna no desenho original da NEDV.
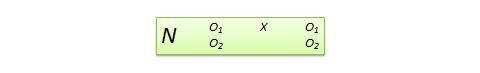
Figure 10.13. NEDV design.
Perigos da Investigação Experimental
A investigação experimental é um dos mais difíceis desenhos de investigação, e não deve ser tomada de ânimo leve. Este tipo de investigação é muitas vezes melhor com uma multiplicidade de problemas metodológicos. Em primeiro lugar, embora a investigação experimental requeira teorias para enquadrar hipóteses para testes, grande parte da investigação experimental actual é ateórica. Sem teorias, as hipóteses testadas tendem a ser ad hoc, possivelmente ilógicas, e sem sentido. Em segundo lugar, muitos dos instrumentos de medição utilizados na investigação experimental não são testados quanto à fiabilidade e validade, e são incomparáveis entre estudos. Consequentemente, os resultados gerados pela utilização de tais instrumentos são também incomparáveis. Terceiro, muitas investigações experimentais utilizam desenhos de investigação inadequados, tais como variáveis dependentes irrelevantes, sem efeitos de interacção, sem controlos experimentais, e estímulos não equivalentes entre grupos de tratamento. Os resultados de tais estudos tendem a carecer de validade interna e são altamente suspeitos. Em quarto lugar, os tratamentos (tarefas) utilizados na investigação experimental podem ser diversos, incomparáveis e inconsistentes entre estudos e por vezes inapropriados para a população sujeita. Por exemplo, os estudantes de graduação são frequentemente solicitados a fingir que são gestores de marketing e solicitados a realizar uma tarefa complexa de atribuição de orçamento na qual não têm qualquer experiência ou especialização. A utilização de tais tarefas inadequadas, introduz novas ameaças à validade interna (ou seja, o desempenho do sujeito pode ser um artefacto do conteúdo ou dificuldade da definição da tarefa), gera resultados que são não-interpretáveis e sem sentido, e torna impossível a integração dos resultados entre estudos.
A concepção de tratamentos experimentais adequados é uma tarefa muito importante na concepção experimental, porque o tratamento é a razão de ser do método experimental, e nunca deve ser apressado ou negligenciado. Para conceber uma tarefa adequada e apropriada, os investigadores devem utilizar tarefas prevalecentes, se disponíveis, realizar verificações de manipulação do tratamento para verificar a adequação de tais tarefas (através do interrogatório dos sujeitos após a realização da tarefa atribuída), realizar testes-piloto (repetidamente, se necessário), e em caso de dúvida, utilizar tarefas mais simples e familiares para a amostra de inquiridos do que tarefas complexas ou desconhecidas.
Em resumo, este capítulo introduziu conceitos-chave no método de investigação de concepção experimental e introduziu uma variedade de verdadeiras concepções experimentais e quase-experimentais. Embora estes desenhos variem muito na validade interna, os desenhos com menos validade interna não devem ser ignorados e podem por vezes ser úteis em circunstâncias específicas e contingências empíricas.