Desenvolvimento da Distribuição Boltzmann
Métodos estatísticos tornam-se uma forma mais precisa de estudar a natureza quando o número de partículas é grande. Assim, esperamos que a descrição das velocidades das moléculas de um gás seja de facto a distribuição mais provável, uma vez que estamos a lidar com números de partículas na gama do número de Avogadro. Mas esta distribuição mais provável (a distribuição Maxwell-Boltzmann) está sujeita a restrições, nomeadamente que o número de partículas é constante e que a energia total é constante (conservação de energia). A maximização da distribuição de probabilidade sujeita a essas restrições em geral é uma tarefa matemática formidável (ver Richtmyer, et al., por exemplo). Uma forma de abordar a solução de uma forma mais intuitiva é lidar com um exemplo físico que conhecemos – nomeadamente a física de uma atmosfera sob a influência da gravidade, tal como reflectida na fórmula barométrica. O tratamento seguinte segue o desenvolvimento por Rohlf.
Nesta abordagem fazemos uso do facto de que a energia cinética média das moléculas pode ser expressa em termos da temperatura cinética. Além disso, sabemos que a conservação de energia neste caso envolve apenas o equilíbrio da energia cinética e da energia potencial gravitacional, desde que tratemos a atmosfera como um gás ideal.
Da expressão para a temperatura cinética
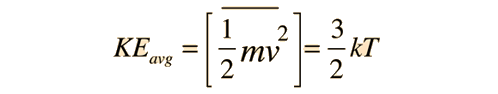>br>>>temos uma expressão experimentalmente testada para a energia cinética molecular. Na fórmula barométrica:
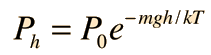
temos uma descrição de um sistema de gás ideal que pode ser usado para ajudar a desenvolver um argumento de plausibilidade para a distribuição da velocidade Maxwell. Os passos neste processo são os seguintes:
>p>>Relate particle velocity to height.br>>p>Relate particle flux to the velocity distribution.>br>>p>Relate velocity distribution to the barometric formula.br>>p>Calcular a distribuição de velocidade e normalizá-la.>br>
Para uma direcção no espaço este processo produz a expressão:
>p> e quando todas as direcções de velocidade estão incluídas, torna-se a relação de distribuição de velocidade Maxwell:
 |
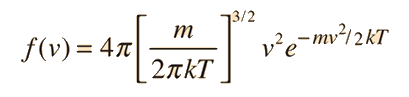Porquê esta relação é inclinada para velocidades mais elevadas, enquanto a acima referida não é? |
>p> Deve notar-se que embora tenhamos utilizado uma situação física dependente da gravidade para obter a distribuição da velocidade, a gravidade não aparece no resultado final. Ou seja, o resultado obtido é geral, não contendo g. A fórmula barométrica foi simplesmente utilizada como uma construção para relacionar a distribuição de velocidade com restrições de energia e número de partículas.