Diferentes tipos de ângulos existem na natureza, e cada um deles tem muita importância na nossa vida diária.
Por exemplo, arquitectos e engenheiros usam ângulos ao projectar máquinas, edifícios, estradas, e pontes.
No desporto, os atletas usam ângulos para melhorar o seu desempenho. Por exemplo, uma pessoa deve rodar com o disco num determinado ângulo para o atirar para longe, em poucas palavras. No futebol, deve usar um determinado ângulo para passar a bola ao jogador seguinte.
Carpinteiros e artesãos também usam ângulos para fabricar objectos tais como sofás, mesas, cadeiras, baldes, etc. Os artistas usam ângulos para esboçar retratos e pinturas. Os estilistas de moda também usam ângulos para trazer certos com os melhores trajes. Por estas razões, é, portanto, necessário conhecer os diferentes tipos de ângulos.
(Para percorrer a explicação básica dos ângulos, pode consultar o artigo anterior, “Ângulos”.”)
Diferentes tipos de ângulos
Angulos são classificados com base em:
- Magnitude
- Rotação
Classificação de ângulos com base na sua magnitude
Existem sete tipos de ângulos com base na sua medição de graus. Eles incluem:
- Ângulos de zero
- Ângulos agudos
- Ângulos rectos
- Ângulos de dúvida
- Ângulos de visão
- Ângulos de reflexo
- Ângulo completo
Ângulo zero
Um ângulo zero (0°) é um ângulo formado quando ambos os braços do ângulo se encontram na mesma posição.
Ilustração:

∠ RPQ = 0° (ângulo zero)
Acute Angle
Um ângulo agudo é um ângulo que é superior a 0° mas inferior a 90°. Exemplos comuns de ângulos agudos incluem: 15°, 30°, 45°, 60°, etc.
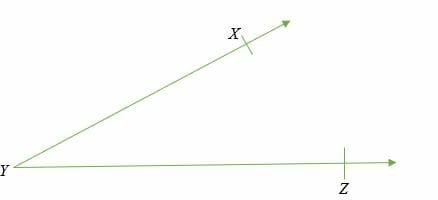
∠ XYZ é superior a 0° mas inferior a 90° (ângulo agudo)
90º Ângulo
Um ângulo de 90º, também conhecido como ângulo recto, é um ângulo cuja medida é igual a 90º é chamado ângulo recto. Os ângulos rectos são representados pelo desenho de uma pequena caixa quadrada entre os braços de um ângulo.
Ilustração:
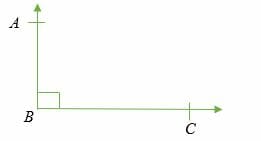
∠ ABC = 90° (ângulo recto)
Haverá um artigo inteiro sobre triângulos rectos na próxima secção (de Triângulos).
Ângulo de Dívida
Um ângulo obtuso é um tipo de ângulo cujo grau de medição é superior a 90° mas inferior a 180°. Exemplos de ângulos obtusos são: 100°, 120°, 140°, 160°, 170°, etc.

∠ O PQR é um ângulo obtuso porque é inferior a 180° e superior a 90°.
Ângulo de recta
Como o nome sugere, um ângulo recto é um ângulo cuja medida é igual a 180° (linha recta)
Ilustração:

∠ XYZ =180° (ângulo recto)
Ângulo de retrocesso
Ângulos de retrocesso são os tipos de ângulos cujo grau de medição é superior a 180° mas inferior a 360°. Exemplos comuns de ângulos reflexos são; 200°, 220°, 250°, 300°, 350°, etc.
Ilustração:

∠ PQR é superior a 180° mas inferior a 360°
Angulo Completo
Um ângulo completo é igual a 360°. 1 volta é igual a 360°.
Ilustração:
p>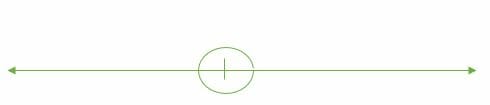
Classificação dos ângulos com base na rotação
Baseado na direcção da rotação, os ângulos podem ser classificados em duas categorias, nomeadamente
- Ângulos positivos
- Ângulos negativos
Ângulos positivos
Ângulos positivos são os tipos de ângulos cujas medidas são tiradas no sentido contrário ao dos ponteiros do relógio a partir da base.
Ângulos negativos
Ângulos negativos são medidos no sentido dos ponteiros do relógio a partir da base.
Outros tipos de ângulos
Parte dos ângulos discutidos acima, existem outros tipos de ângulos conhecidos como ângulos de pares. São chamados ângulos de par porque aparecem em pares para mostrar uma determinada propriedade. Estes são:
- Adjacent ângulos têm o mesmo vértice e braço.
- Ângulos complementares: Ângulos de par que somam até 90º.
- Ângulos suplementares: Ângulos de par cuja soma de ângulos é igual a 180º.
- Ângulos verticalmente opostos. Ângulos verticalmente opostos são iguais.
- Alternate Interior Angles: Ângulos interiores alternados são ângulos de par formados quando uma linha intersecta duas linhas paralelas. Ângulos interiores alternados são sempre iguais um ao outro.
- Alternar Ângulos Exteriores: Os ângulos exteriores alternados são simplesmente ângulos verticais dos ângulos interiores alternados. Os ângulos exteriores alternados são equivalentes.
- Ângulos correspondentes: Os ângulos correspondentes são ângulos de par formados quando uma linha intersecta um par de linhas paralelas. Os ângulos correspondentes são também equivalentes.
Vimos uma breve visão geral dos diferentes tipos de ângulos. A seguir, veremos os artigos detalhados sobre os tipos de ângulos mais comuns (ângulos complementares, ângulos suplementares, etc.).