Um teste t é um teste estatístico que é utilizado para comparar os meios de dois grupos. É frequentemente utilizado em testes de hipóteses para determinar se um processo ou tratamento tem realmente um efeito na população de interesse, ou se dois grupos são diferentes um do outro.
Você quer saber se o comprimento médio das pétalas das flores da íris difere de acordo com a sua espécie. Encontram-se duas espécies diferentes de íris que crescem num jardim e medem 25 pétalas de cada espécie. Pode testar a diferença entre estes dois grupos usando um teste t.
- A hipótese nula (H0) é que a verdadeira diferença entre estes meios de grupo é zero.
- A hipótese alternativa (Ha) é que a diferença verdadeira é diferente de zero.
Quando se usa um teste t
Um teste t só pode ser usado quando se comparam as médias de dois grupos (também conhecido como comparação em pares). Se quiser comparar mais de dois grupos, ou se quiser fazer múltiplas comparações de pares, use um teste ANOVA ou um teste post-hoc.
O teste t é um teste paramétrico de diferença, o que significa que faz as mesmas suposições sobre os seus dados que outros testes paramétricos. O teste t assume os seus dados:
- são independentes
- são (aproximadamente) normalmente distribuídos.
- têm uma quantidade de variação semelhante dentro de cada grupo a ser comparado (a.k.a. homogeneidade de variância)
se os seus dados não se enquadrarem nestas suposições, pode tentar uma alternativa não paramétrica ao teste t, tal como o teste Wilcoxon Signed-Rank para dados com variâncias desiguais.
Que tipo de teste t devo utilizar?
Ao escolher um teste t, terá de considerar duas coisas: se os grupos a serem comparados provêm de uma única população ou de duas populações diferentes, e se pretende testar a diferença numa direcção específica.
Uma amostra, duas amostras, ou teste t emparelhado?
- Se os grupos provêm de uma única população (por exemplo, medindo antes e depois de um tratamento experimental), realize um teste t emparelhado.
- Se os grupos provêm de duas populações diferentes (por exemplo, duas espécies diferentes, ou pessoas de duas cidades separadas), realize um teste t de duas amostras (também conhecido como teste t independente).
- Se existe um grupo a ser comparado com um valor padrão (por exemplo, um grupo de duas populações diferentes), realize um teste t de duas amostras (também conhecido como teste t independente).
- Se existe um grupo a ser comparado com um valor padrão (por exemplo, um grupo de duas populações diferentes), realize um teste t de duas amostras (também conhecido como teste t independente).
g. comparar a acidez de um líquido com um pH neutro de 7), realizar um teste t de uma amostra.
Teste t de uma ou duas caudas?
- Se apenas se importa se as duas populações são diferentes uma da outra, realizar um teste t de duas caudas.
- Se quiser saber se uma média populacional é maior ou menor que a outra, realizar um teste t de uma cauda.
No seu teste para saber se o comprimento das pétalas difere por espécie:
- As suas observações provêm de duas populações separadas (espécies separadas), pelo que efectua um teste t de duas amostras.
- Você não se importa com a direcção da diferença, apenas se existe uma diferença, por isso opta por utilizar um teste t de duas caudas.
Realizar um t-teste
O teste t estima a verdadeira diferença entre dois grupos significa utilizar a razão da diferença nas médias dos grupos sobre o erro-padrão agrupado de ambos os grupos. Pode calculá-lo manualmente utilizando uma fórmula, ou utilizar software de análise estatística.
Fórmula do teste t
A fórmula para o teste t de duas amostras (também conhecido como o teste t de Aluno) é mostrada abaixo.
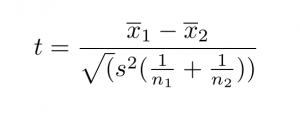
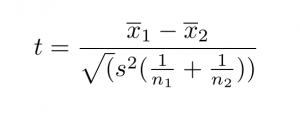
Nesta fórmula, t é o valor t, x1 e x2 são os meios dos dois grupos a serem comparados, s2 é o erro padrão combinado dos dois grupos, e n1 e n2 é o número de observações em cada um dos grupos.
Um valor t maior mostra que a diferença entre as médias dos grupos é maior do que o erro padrão agrupado, indicando uma diferença mais significativa entre os grupos.
Pode comparar o seu valor t calculado com os valores num gráfico de valores críticos para determinar se o seu valor t é maior do que o que seria de esperar por acaso. Se assim for, pode rejeitar a hipótese nula e concluir que os dois grupos são de facto diferentes.
Função de teste t no software estatístico
O software estatístico mais importante (R, SPSS, etc.) inclui uma função de teste t. Esta função integrada tomará os seus dados brutos e calculará o valor t. Depois compará-la-á com o valor crítico, e calculará um valor p. Desta forma, pode ver rapidamente se os seus grupos são estatisticamente diferentes.
Na sua comparação de comprimentos de pétalas de flores, decide realizar o seu teste t usando R. O código é assim:
Download o conjunto de dados para praticar por si próprio.
Dados da amostra
Interpretando os resultados do teste
Se efectuar o teste t para a sua hipótese de flor em R, receberá o seguinte resultado:
p>

O resultado fornece:
- Uma explicação do que está a ser comparado, chamada dados na tabela de resultados.
- O valor t: -33.719. Note-se que é negativo; isto é óptimo! Na maioria dos casos, só nos interessa o valor absoluto da diferença, ou a distância de 0. Não importa qual a direcção.
- Os graus de liberdade: 30.196. Os graus de liberdade estão relacionados com o tamanho da sua amostra, e mostram quantos pontos de dados ‘livres’ estão disponíveis no seu teste para fazer comparações. Quanto maiores forem os graus de liberdade, melhor funcionará o seu teste estatístico.
- O valor p: 2,2e-16 (ou seja, 2,2 com 15 zeros à frente). Isto descreve a probabilidade de ver um valor t tão grande como este por acaso.
- uma declaração da hipótese alternativa (Ha). Neste teste, o Ha é que a diferença não é 0,
- O intervalo de confiança de 95%. Este é o intervalo de números dentro do qual a verdadeira diferença de meios será de 95% do tempo. Isto pode ser alterado de 95% se desejar um intervalo maior ou menor, mas 95% é muito comumente utilizado.
- O comprimento médio das pétalas para cada grupo.
Apresentar os resultados de um teste t
Ao comunicar os resultados do seu teste t, os valores mais importantes a incluir são o valor t, o valor p, e os graus de liberdade para o teste. Estes comunicarão ao seu público se a diferença entre os dois grupos é estatisticamente significativa (ou seja, que é pouco provável que tenha acontecido por acaso).
Pode também incluir as estatísticas sumárias dos grupos a serem comparados, nomeadamente a média e o desvio padrão. Em R, o código para calcular a média e o desvio padrão dos dados parece-se com isto:
flower.data %>%
group_by(Species) %>%
summarize(mean_length = mean(Petal.Length),
sd_length = sd(Petal.Length))
No nosso exemplo, relataria os resultados desta forma:
Perguntas frequentes sobre os testes t
Um teste t é um teste estatístico que compara os meios de duas amostras. É utilizado no teste de hipóteses, com uma hipótese nula de que a diferença na média do grupo é zero e uma hipótese alternativa de que a diferença na média do grupo é diferente de zero.
Um teste t mede a diferença nas médias do grupo dividida pelo erro padrão combinado das duas médias do grupo.
Desta forma, calcula um número (o valor t) ilustrando a magnitude da diferença entre as duas médias do grupo, e estima a probabilidade de esta diferença existir puramente por acaso (valor p).
A sua escolha do teste t depende de se está a estudar um ou dois grupos, e se se preocupa com a direcção da diferença no grupo significa.
Se estiver a estudar um grupo, utilize um teste t emparelhado para comparar a média do grupo ao longo do tempo ou após uma intervenção, ou utilize um teste t de uma amostra para comparar a média do grupo com um valor padrão. Se estiver a estudar dois grupos, utilize um teste t de duas amostras.
Se quiser saber apenas se existe uma diferença, utilize um teste de duas amostras. Se quiser saber se a média de um grupo é maior ou menor que a do outro, utilize um teste de uma cauda à esquerda ou à direita.
Um teste t de uma amostra é utilizado para comparar uma única população com um valor padrão (por exemplo, para determinar se a duração média de vida de uma cidade específica é diferente da média do país).
Um teste t emparelhado é utilizado para comparar uma única população antes e depois de alguma intervenção experimental ou em dois pontos diferentes no tempo (por exemplo, medir o desempenho do aluno num teste antes e depois de ser ensinado o material).
Um teste t não deve ser usado para medir diferenças entre mais de dois grupos, porque a estrutura de erro de um teste t subestima o erro real quando muitos grupos estão a ser comparados.
Se quiser comparar os meios de vários grupos ao mesmo tempo, é melhor usar outro teste estatístico como o ANOVA ou um teste post-hoc.
