Desarrollo de la distribución de Boltzmann
Los métodos estadísticos se convierten en una forma más precisa de estudiar la naturaleza cuando el número de partículas es grande. Así que esperamos que la descripción de las velocidades de las moléculas en un gas sea de hecho la distribución más probable, ya que estamos tratando con números de partículas en el rango del número de Avogadro. Pero esta distribución más probable (la distribución de Maxwell-Boltzmann) está sujeta a restricciones, a saber, que el número de partículas es constante y que la energía total es constante (conservación de la energía). Maximizar la distribución de probabilidad sujeta a esas restricciones en general es una tarea matemática formidable (véase Richtmyer, et al., por ejemplo). Una forma de abordar la solución de manera más intuitiva es tratar un ejemplo físico que conocemos, a saber, la física de una atmósfera bajo la influencia de la gravedad, tal como se refleja en la fórmula barométrica. El siguiente tratamiento sigue el desarrollo de Rohlf.
En este enfoque hacemos uso del hecho de que la energía cinética media de las moléculas se puede expresar en términos de la temperatura cinética. Además, sabemos que la conservación de la energía en este caso implica sólo el equilibrio de la energía cinética y la energía potencial gravitatoria siempre que tratemos la atmósfera como un gas ideal.
A partir de la expresión para la temperatura cinética
tenemos una expresión comprobada experimentalmente para la energía cinética molecular. En la fórmula barométrica:
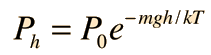
tenemos una descripción de un sistema de gas ideal que puede utilizarse para ayudar a desarrollar un argumento de plausibilidad para la distribución de velocidad de Maxwell. Los pasos de este proceso son los siguientes:
Relacionar la velocidad de las partículas con la altura.
Relacionar el flujo de las partículas con la distribución de velocidades.
Relacionar la distribución de velocidades con la fórmula barométrica.
Calcular la distribución de velocidades y normalizarla.
Para una dirección en el espacio este proceso arroja la expresión:

y cuando se incluyen todas las direcciones de velocidad, se convierte en la relación de distribución de velocidad de Maxwell:
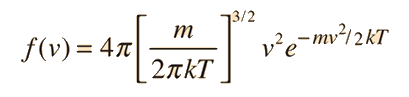 |
¿Por qué esta relación está sesgada hacia las velocidades más altas mientras que la de arriba no lo está? |
Hay que tener en cuenta que aunque hemos utilizado una situación física dependiente de la gravedad para obtener la distribución de velocidades, la gravedad no aparece en el resultado final. Es decir, el resultado obtenido es general, no contiene g. La fórmula barométrica se utilizó simplemente como una construcción para relacionar la distribución de velocidades con las restricciones de energía y número de partículas.