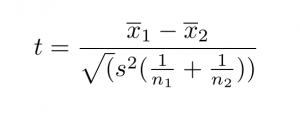Una introducción a las pruebas t

Una prueba t es una prueba estadística que se utiliza para comparar las medias de dos grupos. Se suele utilizar en las pruebas de hipótesis para determinar si un proceso o tratamiento tiene realmente un efecto sobre la población de interés, o si dos grupos son diferentes entre sí.

Cuándo utilizar una prueba t

Una prueba t sólo puede utilizarse cuando se comparan las medias de dos grupos (también conocida como comparación por pares). Si quiere comparar más de dos grupos, o si quiere hacer múltiples comparaciones por pares, utilice una prueba ANOVA o una prueba post-hoc.

La prueba t es una prueba paramétrica de diferencia, lo que significa que hace las mismas suposiciones sobre sus datos que otras pruebas paramétricas. La prueba t asume que sus datos:

1. son independientes
2. están (aproximadamente) distribuidos normalmente.
3. Tienen una cantidad similar de varianza dentro de cada grupo que se compara (a.k.a. homogeneidad de la varianza)

Si sus datos no se ajustan a estos supuestos, puede probar una alternativa no paramétrica a la prueba t, como la prueba de rango con signo de Wilcoxon para datos con varianzas desiguales.

¿Qué tipo de prueba t debo utilizar?

Al elegir una prueba t, deberá tener en cuenta dos cosas: si los grupos que se comparan proceden de una única población o de dos poblaciones diferentes, y si desea probar la diferencia en una dirección específica.

¿Una muestra, dos muestras o una prueba t pareada?

• Si los grupos proceden de una sola población (por ejemplo, midiendo antes y después de un tratamiento experimental), realice una prueba t emparejada.
• Si los grupos proceden de dos poblaciones diferentes (por ejemplo, dos especies diferentes, o personas de dos ciudades distintas), realice una prueba t de dos muestras (también conocida como prueba t independiente).
• Si hay un grupo que se está comparando con un valor estándar (por ej.p. ej., comparar la acidez de un líquido con un pH neutro de 7), realice una prueba t de una muestra.

Prueba t de una o dos colas?

• Si sólo le interesa saber si las dos poblaciones son diferentes entre sí, realice una prueba t de dos colas.
• Si quiere saber si la media de una población es mayor o menor que la otra, realice una prueba t de una cola.
En su prueba de si la longitud de los pétalos difiere según la especie:
• Sus observaciones provienen de dos poblaciones separadas (especies separadas), por lo que realiza una prueba t de dos muestras.
• No te importa la dirección de la diferencia, sólo si hay una diferencia, así que eliges usar una prueba t de dos colas.

¿Cuál es tu puntuación de plagio?

Compara tu trabajo con más de 60 mil millones de páginas web y 30 millones de publicaciones.

• El mejor corrector de plagio de 2020
• Informe de plagio & porcentaje
• La mayor base de datos de plagio
• .

Scribbr Plagiarism Checker



Realizar un t-test

La prueba t estima la verdadera diferencia entre las medias de dos grupos utilizando el cociente de la diferencia de las medias de los grupos sobre el error estándar agrupado de ambos grupos. Se puede calcular manualmente mediante una fórmula, o utilizar un software de análisis estadístico.

Fórmula de la prueba t

A continuación se muestra la fórmula de la prueba t de dos muestras (también conocida como prueba t de Student).





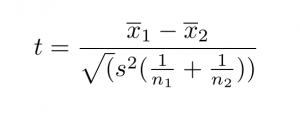
En esta fórmula, t es el valor t, x1 y x2 son las medias de los dos grupos que se comparan, s2 es el error estándar conjunto de los dos grupos, y n1 y n2 son el número de observaciones en cada uno de los grupos.

Un valor t mayor muestra que la diferencia entre las medias de los grupos es mayor que el error estándar agrupado, lo que indica una diferencia más significativa entre los grupos.

Puede comparar su valor t calculado con los valores de una tabla de valores críticos para determinar si su valor t es mayor de lo que se esperaría por azar. Si es así, puede rechazar la hipótesis nula y concluir que los dos grupos son, de hecho, diferentes.

Función de prueba t en el software estadístico

La mayoría del software estadístico (R, SPSS, etc.) incluye una función de prueba t. Esta función incorporada tomará sus datos en bruto y calculará el valor t. A continuación, lo comparará con el valor crítico y calculará un valor p. De esta manera, puede ver rápidamente si sus grupos son estadísticamente diferentes.

En su comparación de las longitudes de los pétalos de las flores, decide realizar su prueba t utilizando R. El código tiene el siguiente aspecto:

t.test(Pétalo.Longitud ~ Especie, datos = flor.datos)

Descargue el conjunto de datos para practicar por sí mismo.

Conjunto de datos de la muestra

Interpretación de los resultados de la prueba

Si realiza la prueba t para su hipótesis de la flor en R, recibirá la siguiente salida:





La salida proporciona:

1. Una explicación de lo que se está comparando, llamada datos en la tabla de salida.
2. El valor t: -33,719. Observe que es negativo; ¡esto está bien! En la mayoría de los casos, sólo nos importa el valor absoluto de la diferencia, o la distancia desde 0. No importa la dirección.
3. Los grados de libertad: 30,196. Los grados de libertad están relacionados con el tamaño de la muestra, y muestran cuántos puntos de datos «libres» están disponibles en su prueba para hacer comparaciones. Cuanto mayores sean los grados de libertad, mejor funcionará su prueba estadística.
4. El valor p: 2,2e-16 (es decir, 2,2 con 15 ceros delante). Esto describe la probabilidad de que usted vea un valor t tan grande como éste por casualidad.
5. Una declaración de la hipótesis alternativa (Ha). En esta prueba, la Ha es que la diferencia no es 0.
6. El intervalo de confianza del 95%. Este es el rango de números dentro del cual la verdadera diferencia de medias estará el 95% de las veces. Esto se puede cambiar del 95% si se desea un intervalo más grande o más pequeño, pero el 95% se utiliza muy comúnmente.
7. La longitud media de los pétalos para cada grupo.
Desde la tabla de salida, podemos ver que la diferencia de medias para nuestros datos de la muestra es -4,084 (1,456 – 5,540), y el intervalo de confianza muestra que la verdadera diferencia de medias está entre -3,836 y -4,331. Así, el 95% de las veces, la verdadera diferencia de medias será diferente de 0. Nuestro valor p de 2,2e-16 es mucho menor que 0,05, por lo que podemos rechazar la hipótesis nula de ausencia de diferencias y decir con un alto grado de confianza que la verdadera diferencia de medias no es igual a cero.

Presentación de los resultados de una prueba t

Al informar de los resultados de su prueba t, los valores más importantes que debe incluir son el valor t, el valor p y los grados de libertad de la prueba. Estos comunicarán a su audiencia si la diferencia entre los dos grupos es estadísticamente significativa (es decir, que es poco probable que haya ocurrido por casualidad).

También puede incluir los estadísticos de resumen para los grupos que se comparan, a saber, la media y la desviación estándar. En R, el código para calcular la media y la desviación estándar de los datos tiene el siguiente aspecto:

Flor.data %>%
group_by(Species) %>%
summarize(mean_length = mean(Petal.Length),
sd_length = sd(Petal.Length))

En nuestro ejemplo, se informarían los resultados así:

La diferencia en la longitud de los pétalos entre la especie de iris 1 (Media = 1,46; SD = 0,206) y la especie de iris 2 (Media = 5.54; SD = 0,569) fue significativa (t (30) = -33,7190; p < 2,2e-16).

Preguntas frecuentes sobre las pruebas t

¿Qué es una prueba t?
Una prueba t es una prueba estadística que compara las medias de dos muestras. Se utiliza en la comprobación de hipótesis, con una hipótesis nula de que la diferencia de las medias de los grupos es cero y una hipótesis alternativa de que la diferencia de las medias de los grupos es diferente de cero.
¿Qué mide una prueba t?
Una prueba t mide la diferencia de las medias de los grupos dividida por el error estándar agrupado de las dos medias de los grupos.
De este modo, calcula un número (el valor t) que ilustra la magnitud de la diferencia entre las dos medias de los grupos que se comparan, y estima la probabilidad de que esta diferencia exista por pura casualidad (valor p).
¿Qué prueba t debo utilizar?
La elección de la prueba t depende de si está estudiando un grupo o dos grupos, y de si le preocupa la dirección de la diferencia en las medias de los grupos.
Si está estudiando un grupo, utilice una prueba t pareada para comparar la media del grupo a lo largo del tiempo o después de una intervención, o utilice una prueba t de una muestra para comparar la media del grupo con un valor estándar. Si está estudiando dos grupos, utilice una prueba t de dos muestras.
Si quiere saber sólo si existe una diferencia, utilice una prueba de dos colas. Si quiere saber si la media de un grupo es mayor o menor que la del otro, utilice una prueba de una cola a la izquierda o a la derecha.
¿Cuál es la diferencia entre una prueba t de una muestra y una prueba t pareada?
Una prueba t de una muestra se utiliza para comparar una única población con un valor estándar (por ejemplo, para determinar si la media de vida de una ciudad específica es diferente de la media del país).
Una prueba t pareada se utiliza para comparar una única población antes y después de alguna intervención experimental o en dos momentos diferentes (por ejemplo, medir el rendimiento de los estudiantes en un examen antes y después de que se les enseñe el material).
¿Puedo utilizar una prueba t para medir la diferencia entre varios grupos?
No se debe utilizar una prueba t para medir las diferencias entre más de dos grupos, porque la estructura de error de una prueba t subestimará el error real cuando se comparen muchos grupos.
Si quiere comparar las medias de varios grupos a la vez, es mejor utilizar otra prueba estadística como ANOVA o una prueba post-hoc.