Álgebra sin límites

Objetivos de aprendizaje

Explicar cómo la ecuación de una circunferencia describe sus propiedades

Puntos clave

Puntos clave

• Se define una circunferencia como el conjunto de puntos que están a una distancia fija de un punto central.
• La fórmula de la distancia se puede extender directamente a la definición de un círculo observando que el radio es la distancia entre el centro de un círculo y el borde.
• La ecuación general de una circunferencia, centrada en \left(a,b\right) con radio r, es el conjunto de todos los puntos \left(x,y\right) tales que \left(x-a\right)^2+\left(y-b\right)^2=r^2.
• Pi (\pi) es el cociente entre la circunferencia de un círculo y su diámetro.

Términos clave

• Diámetro: Dos veces el radio de un círculo.
• Área: La superficie interior de un círculo, dada por A = \pi r^2.
• Círculo: Figura geométrica bidimensional, formada por el conjunto de todos aquellos puntos de un plano que distan igualmente de otro punto.
• Radio: Segmento de línea entre cualquier punto de la circunferencia de un círculo y su centro.

La definición de círculo es tan sencilla como su forma. Un círculo es el conjunto de todos los puntos que están a una determinada distancia de un punto central. Esta definición es la que nos da el concepto de radio de una circunferencia, que es igual a esa determinada distancia.

Dado que sabemos que una circunferencia es el conjunto de puntos a una distancia fija de un punto central, vamos a ver cómo podemos construir una circunferencia en un plano de coordenadas cartesianas con las variables x e y. Para encontrar la fórmula de la misma, supongamos que el centro es el punto \a(a,b\a). Según la fórmula de la distancia, la distancia c del punto \left(a,b\right) a cualquier otro punto \left(x,y\right) es:

displaystyle{c = \sqrt{ \left(x-a\right)^2 + \left(y-b\right)^2}

Si ahora elevamos al cuadrado esta ecuación por ambos lados, tenemos:

\displaystyle{c^{2} = \left(x-a\right)^{2}+\left(y-b\right)^{2}

Recuerda que la distancia entre el centro \left(a,b\right) y cualquier punto \left(x,y\right) de la circunferencia es esa distancia fija, que se llama radio. Así que vamos a cambiar esta ecuación para que utilice r en lugar de c.

Estilo de visualización{r^{2} = \left(x-a\right)^{2}+\left(y-b\right)^{2}

Esta es la fórmula general para un círculo con centro \left(a,b\right) y radio r. Observa que lo único que hemos hecho es reordenar ligeramente la ecuación de la fórmula de la distancia.



Gráfico de una circunferencia: La circunferencia con centro \left(a,b\right) se representa gráficamente en el plano cartesiano.

Partes de una circunferencia

Ahora que tenemos una base algebraica para la circunferencia, vamos a conectarla con lo que ya sabemos sobre algunas partes diferentes de la circunferencia.

Diámetro

El diámetro es cualquier línea recta que pasa por el centro de la circunferencia. Es igual al doble del radio, por lo que:

d = 2r

Circunferencia

La circunferencia es la longitud del recorrido alrededor del círculo. Algebraicamente viene dada por:

c = 2\pi r

o equivalentemente por c = \pi d. El número \pi (pi) viene definido por esta relación. Es el cociente entre la circunferencia de cualquier círculo y su propio diámetro.

Área

El área de un círculo viene dada por:

A = \pi r^2

Nota que el radio es el único parámetro que define el tamaño de cualquier círculo concreto, y por tanto es la única variable de la que depende el área.

Introducción a las elipses

Entiende la ecuación de una elipse como un círculo estirado.

Objetivos de aprendizaje

Conectar la ecuación de una elipse con la ecuación de un círculo con factores de estiramiento

Puntos clave

Puntos clave

• Una elipse y un círculo son ejemplos de secciones cónicas.
• Un círculo es un caso especial de una elipse, con el mismo radio para todos los puntos.
• Al estirar un círculo en la dirección x o y, se crea una elipse.

Una elipse es una de las formas llamadas secciones cónicas, que se forma por la intersección de un plano con un cono circular recto. La ecuación general de una elipse centrada en \left(h,k\right) es:

{displaystyle{\frac{\left(x-h\right)^2}{a^2} + \frac{izquierda(y-k\derecha)^2}{b^2} = 1}

cuando el eje mayor de la elipse es horizontal.



Elipse: Una elipse es una sección cónica, formada por la intersección de un plano con un cono circular recto.

En la mayoría de las definiciones de las secciones cónicas, el círculo se define como un caso especial de la elipse, cuando el plano es paralelo a la base del cono. Sin embargo, también es posible comenzar con la definición de un círculo y utilizar transformaciones gráficas para llegar a la fórmula general de una elipse.

Recordemos que un círculo se define como el conjunto de todos los puntos que equidistan de un centro común. Para simplificar, elegiremos que ese centro sea \left(0,0\right), el origen del plano x-y. Entonces podemos escribir la ecuación del círculo de esta manera:

x^2 + y^2 = r^2

En esta ecuación, r es el radio del círculo. Un círculo sólo tiene un radio: la distancia del centro a cualquier punto es la misma. Para convertir nuestro círculo en una elipse, tendremos que estirar o apretar el círculo para que las distancias dejen de ser las mismas. En primer lugar, vamos a empezar con un círculo específico con el que es fácil trabajar, el círculo centrado en el origen con radio 1.

Para convertirlo en una elipse, debemos distorsionar la forma circular para que deje de ser simétrica entre x e y. Para ello, introducimos un factor de escala en una o ambas coordenadas
x-y. Empecemos dividiendo todas las coordenadas x por un factor a, y por tanto escalando los valores x. Simplemente sustituimos \displaystyle{{frac{x}{a}} en la ecuación en lugar de x. Nota importante: Suponemos que a > 1.

{displaystyle{{izquierda(\frac{x}{a}{derecha)^2 + y^2 = 1}



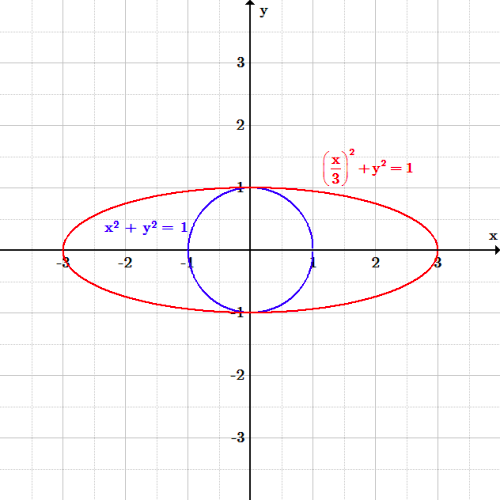
Elipse a lo largo del eje x: La elipse \left( \frac{x}{3} \right)^2 +y^2 = 1 se ha estirado a lo largo del eje x por un factor de 3 en comparación con el círculo x^2 + y^2 = 1.

Cada valor x que resolvía la ecuación antigua debe ahora multiplicarse por a para resolver la nueva ecuación. Esto tiene el efecto de estirar más la elipse en el eje x, porque los valores más grandes de x son ahora las soluciones.

De forma similar, podemos escalar todos los valores de y por un factor b (también asumimos b > 1).

displaystyle {x^2 + \left(\frac{y}{b}\right)^2 = 1}

Ahora todos los valores de y están estirados verticalmente, más alejados del origen.



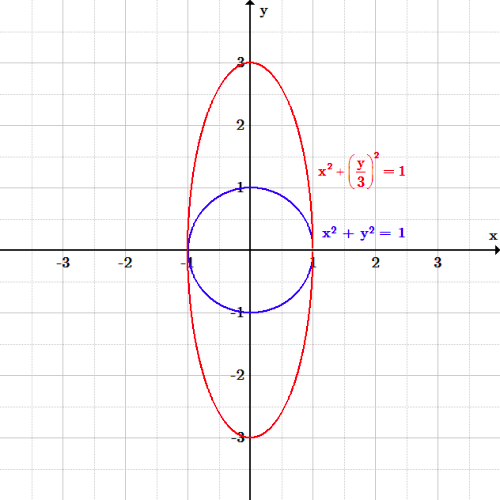
Elipse a lo largo del eje y: La elipse x^2 +\left( \frac{y}{3} \right)^2 = 1 se ha estirado a lo largo del eje y por un factor de 3 en comparación con el círculo x^2 + y^2 = 1.

Si estiramos en las direcciones x e y y distribuimos las potencias de dos a través de los paréntesis, obtenemos:

displaystyle{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1}

que es exactamente la ecuación de una elipse horizontal centrada en el origen.

Si hubiéramos utilizado factores de escala menores que uno, se habría comprimido la forma en lugar de estirarla más.

Partes de una elipse

Las elipses son uno de los tipos de secciones cónicas. Las características específicas de una elipse se pueden determinar a partir de su ecuación.

Objetivos de aprendizaje

Discutir cómo la ecuación de una elipse describe sus propiedades

Puntos clave

Puntos clave

• Una elipse está formada por un plano que interseca un cono en un ángulo con su base.
• Todas las elipses tienen dos puntos focales, o focos. La suma de las distancias de cada punto de la elipse a los dos focos es una constante.
• Todas las elipses tienen un centro y un eje mayor y menor.
• Todas las elipses tienen valores de excentricidad mayores o iguales a cero, y menores que uno.

Ecuación de una elipse

Una elipse es una sección cónica, formada por la intersección de un plano con un cono circular recto. La forma estándar de la ecuación de la elipse es:

Displaystyle{\frac{Izquierda(x-h\ derecha)^2}{a^2} + \frac{izquierda(y-k\ derecha)^2}{b^2} = 1}

si la elipse está orientada horizontalmente, y:

displaystyle{\frac{izquierda(y-k\ derecha)^2}{a^2} + \frac{izquierda(x-h\derecha)^2}{b^2} = 1}

si la elipse está orientada verticalmente. Utilizaremos el caso horizontal para demostrar cómo determinar las propiedades de una elipse a partir de su ecuación, de forma que a se asocie con las coordenadas x, y b con las coordenadas y. Para una elipse vertical, la asociación se invierte.



Diagrama de una elipse: Este diagrama de una elipse horizontal muestra la propia elipse en rojo, el centro C en el origen, los focos en \left(+f,0\right) y \left(-f,0\right), los vértices del eje mayor en \left(+a,0\right) y \left(-a,0\right), los vértices del eje menor en \left(0,+b\right) y \left(0,-b\right). También muestra cómo la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante a 2a (la longitud del eje mayor), y cómo la excentricidad viene determinada por el cociente entre la distancia de un punto de la elipse a uno de los focos y la distancia perpendicular del punto a una recta D llamada directriz, exterior a la elipse y perpendicular al eje mayor.

Partes de una elipse

El centro de la elipse tiene las coordenadas (h,k).

Eje mayor

El eje mayor de la elipse es el mayor ancho que la atraviesa. Para una elipse horizontal, ese eje es paralelo al eje x. El eje mayor tiene una longitud de 2a. Sus puntos extremos son los vértices del eje mayor, con coordenadas (h \pm a, k).

Eje menor

El eje menor de la elipse es la anchura más corta que la atraviesa. Para una elipse horizontal, es paralelo al eje y. El eje menor tiene una longitud de 2b. Sus puntos extremos son los vértices del eje menor, con coordenadas (h, k \pm b).

Focos

Los focos son dos puntos dentro de la elipse que caracterizan su forma y curvatura. Para una elipse horizontal, los focos tienen coordenadas (h \pm c,k), donde la distancia focal c viene dada por

c^2 = a^2 – b^2

Ecentricidad

Todas las secciones cónicas tienen un valor de excentricidad, denotado e. Todas las elipses tienen excentricidades en el rango 0 \leq e < 1. Una excentricidad de cero es el caso especial en el que la elipse se convierte en un círculo. Una excentricidad de 1 es una parábola, no una elipse.

La excentricidad se define como:

displaystyle{e = \frac{c}{a}

o, de forma equivalente:

Estilo de visualización{\begin{align} e &= \frac{{sqrt{a^2 – b^2}{a} &= \sqrt{\frac{a^2 – b^2}{a^2} } &= 1 – \frac{b^2}{a^2} |end{align} } }

Las órbitas de los planetas y sus lunas son elipses con excentricidades muy bajas, es decir, son casi circulares. Las órbitas de los cometas alrededor del sol pueden ser mucho más excéntricas. En el caso de los cometas y los planetas, el sol se encuentra en uno de los focos de sus órbitas elípticas.

Aplicaciones de los círculos y las elipses

Los círculos y las elipses se encuentran en la vida cotidiana, y saber resolver sus ecuaciones es útil en muchas situaciones.

Objetivos de aprendizaje

Describir las aplicaciones de las fórmulas de círculos y elipses a los problemas del mundo real

Los puntos clave

Puntos clave

• La forma estándar de la ecuación de un círculo es \left(x-h\a)^2+\a izquierda(y-k\a)^2=r^2, donde r es el radio, y \left(h,k\right) es la coordenada del punto central.
• La forma estándar de la ecuación de una elipse es \displaystyle{\frac {\left(x-h\right)^2}{a^2}+\frac {\left(y-k\right)^2}{b^2}= 1}, donde \left(h,k\right) es la coordenada del punto central, 2a es la longitud del eje mayor/menor, y 2b es la longitud del eje menor/mayor.
• Si a>b, el eje mayor es paralelo al eje x. Si a<b, el eje mayor es paralelo al eje y (perpendicular al eje x).
• Para determinar los parámetros de una circunferencia o una elipse, primero hay que poner la ecuación en la forma estándar.

Términos clave

• Elipse: Una curva cerrada, el lugar de un punto tal que la suma de las distancias de ese punto a otros dos puntos fijos (llamados focos de la elipse) es constante; equivalentemente, la sección cónica que es la intersección de un cono con un plano que no interseca la base del cono.
• Círculo: Figura geométrica bidimensional, que consiste en el conjunto de todos aquellos puntos de un plano que distan por igual de otro punto.

Los círculos están por todas partes en la vida cotidiana, desde las llantas de los coches hasta los botones de los abrigos, así como en la parte superior de cuencos, vasos y botellas de agua. Las elipses son menos comunes. Un ejemplo son las órbitas de los planetas, pero deberías ser capaz de encontrar el área de un círculo o de una elipse, o la circunferencia de un círculo, a partir de la información que te den en un problema. Los círculos y las elipses son ejemplos de secciones cónicas, que son curvas formadas por la intersección de un plano con un cono.

A continuación se muestran algunos problemas de ejemplo, con las soluciones elaboradas.

Ejercicio 1

Supongamos que eres jardinero y acabas de plantar un montón de flores que quieres regar. El parterre tiene 4 metros de ancho y 4 metros de largo. Usted está utilizando un sistema de aspersión circular, y el agua llega a 6 pies fuera del centro. El aspersor está situado, desde la esquina inferior izquierda del parterre, a 7 pies de altura, y a 6 pies de altura.

1. Si el parterre fuera una gráfica en la que la esquina inferior izquierda fuera el origen, ¿cuál sería la ecuación del círculo?
2. ¿Cuál es el área que está siendo regada por el aspersor?
3. ¿Qué porcentaje del jardín está siendo regado?

Respuesta

Si la esquina inferior izquierda es el origen, tiene coordenadas \a izquierda(0,0\a derecha). A partir de ahí el aspersor está a 6 pies, por lo que la coordenada x del centro es 6. El aspersor está a 7 pies, por lo que la coordenada y del centro es 7. Ergo, el centro del círculo está en la coordenada \left(6,7\right). El agua llega a 6 pies fuera del aspersor, por lo que el radio del círculo es de 6 pies. Por lo tanto, la ecuación de este círculo es:

{displaystyle{{Izquierda(x-6\right)^2+{Izquierda(y-7\right)^2=36}

El área que es regada por el aspersor puede ser etiquetada como A_{sprinkler}, y es:

{displaystyle{{\begin{align} A_{sprinkler} &=pi\cdot r^2\ &=pi\cdot 6^2\ &=36\pi \cdot \align} }

El primer paso para encontrar el porcentaje del jardín que se está regando es comprobar que no cae nada de agua fuera del jardín. El aspersor se encuentra en la coordenada \left(6,7\right), y el radio del aspersor es de 6 pies. Se puede comprobar que el agua no cae fuera del jardín de 15 veces 15.

Una vez que sabemos que el área que se riega está completamente dentro del jardín, el porcentaje del jardín que se riega se puede encontrar dividiendo el área regada por el área total del jardín, y luego multiplicando por 100\%:

displaystyle{\begin{align} Porcentaje_{regado} &==\frac {A_{sprinkler}}{A_{flower bed}}{cdot 100\%} &=\frac {36\pi}{15^2}{cdot 100\%} &=\frac {113.1}{225}{cdot 100\%} &=50.3\%{cdot 100\%}

Ejercicio 2

Ahora, tomemos el camino inverso. (x – 4)^2+(y+8)^2=49 es la ecuación de una circunferencia.

1. ¿Cuáles son las coordenadas del centro de la circunferencia?
2. ¿Cuál es el radio?
3. Dibuja la circunferencia.
4. Encuentra dos puntos de la circunferencia e introdúcelos en la ecuación para asegurarte de que tu dibujo es correcto.

Respuesta

El centro de la circunferencia se puede encontrar comparando la ecuación de este ejercicio con la ecuación de una circunferencia:

Izquierda(x-h\ derecha)^2+Izquierda(y-k\ derecha)^2=r^2

El centro de la circunferencia está en la coordenada \ izquierda(h,k\ derecha), por lo que el centro de la circunferencia de este ejercicio está en \ izquierda(4,-8\ derecha).

El radio de la circunferencia es r. A partir de la ecuación de una circunferencia, \displaystyle{r^2=49}. Por lo tanto:

\NDisplaystyle{{in{align} r^2 &= 49 \N- r &= \sqrt{49} &= 7 }



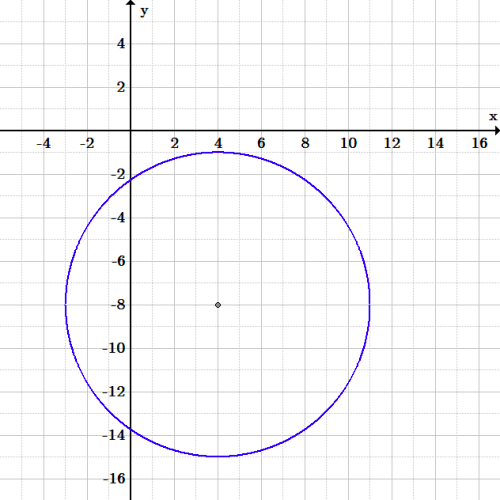
Ejercicio 2 círculo: Gráfica del círculo (x – 4)^2+(y+8)^2=49.

Hay muchos puntos que podrías elegir. Por ejemplo, el punto \a la izquierda(4, -1\a la derecha) está en la parte superior del círculo. Introduciendo esto en la ecuación, obtenemos:

Estilo de visualización \left(x-h\right)^2+\left(y-k\right)^2 &=r^2 \\\\N-(4-4)^2+(-1+8)^2 &= 49 \N-(0)^2 + (7)^2 &= 49 \N-(0)^2 + (7)^2 &= 49 \N-(1).

El lado izquierdo es igual al lado derecho de la ecuación, por lo que este es un punto válido en el círculo.

El punto más a la izquierda del círculo es (-3,-8). Introduciendo esto en la ecuación:

Displaystyle{{comenzar{alinear} |2+Izquierda(y-k\\a la derecha)^2 &=r^2 \a la izquierda(-3-4\a la derecha)^2+Izquierda(-8+8\a la derecha)^2 &= 49 \a (-7)^2 + (0)^2 &= 49 \a }

El lado izquierdo es igual al lado derecho de la ecuación, por lo que este es un punto válido en el círculo.

Ejercicio 3

1. Ponga 2x^2+2y^2+8x+24y+60=0 en la forma estándar del círculo: (x-h)^2+(y-k)^2=r^2.
2. ¿Cuál es el centro y el radio de la circunferencia?
3. Dibuja la circunferencia.
4. Encuentra dos puntos de la circunferencia y enchúfalos en la ecuación para asegurarte de que tu dibujo es correcto.

Respuesta

Primero, divide la ecuación entre el coeficiente de x^2 e y^2, que es 2:

\displaystyle{\begin{align} 2x^2+2y^2+8x+24y+60 &=0 \frac{2x^2+2y^2+8x+24y+60}{2} &=\frac{0}{2} \\ \frac{2x^2}{2}+\frac{2y^2}{2}+\frac{8x}{2}+\frac{24y}{2}+\frac{60}{2} &=\frac{0}{2} \\ x^2+y^2+4x+12y+30 &=0 \N-end{align}} }

A continuación, junta los términos x e y, y lleva el número al lado derecho de la ecuación:

(x^2+4x)+(y^2+12y)=-30

Ahora, completa el cuadrado en ambos paréntesis, restando o añadiendo la constante necesaria a ambos lados de la ecuación:

(x^2+4x+4)+(y^2+12y+36) &=-30+4+36 \\N (x^2+4x+4)+(y^2+12y+36) &= 10 \Nend{align}

Nota que cada término es un cuadrado perfecto, lo que da:

(x+2)^2+(y+6)^2=10

Esto está ahora en la forma estándar para la ecuación de un círculo.

El centro de la circunferencia está en la coordenada \ izquierda(h,k\ derecha), por lo que el centro de la circunferencia en este ejercicio está en \ izquierda(-2,-6\ derecha).

El radio de la circunferencia es r. A partir de la ecuación de una circunferencia, \displaystyle{r^2=10}. Por lo tanto:

\NDisplaystyle{{comenzar{alinear} r^2 &= 10 \N- r &= \sqrt{10} \N – fin {align} }

Está bien dejar el valor de r de esta forma.



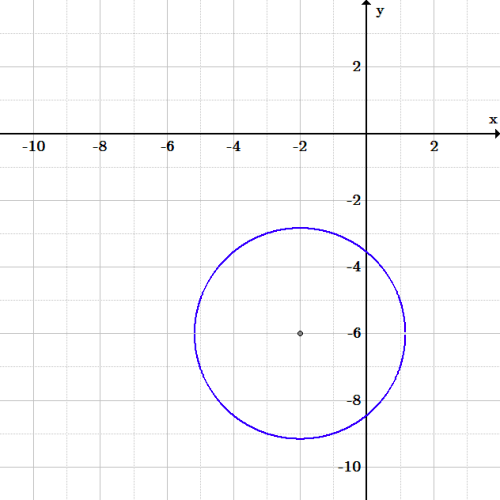
Ejercicio 3 círculo: Gráfica del círculo 2x^2+2y^2+8x+24y+60=0.

Hay muchos puntos que podrías elegir. Por ejemplo, (-5,-5) y (-3, -9):

\NDisplaystyle{\N} (-5+2)^2 + (-5 + 6)^2 &= 10 \N(-3)^2 + (1)^2 &= 10 \N9 + 1 &=10\N10 &= 10 \Nend{align}.

Estilo de visualización (-3+2)^2 + (-9+6)^2 &= 10\N(-1)^2 + (-3)^2 &= 10 \N1 + 9 &= 10 \N &= 10 \Nend{align}. }

Ambos son puntos válidos en la circunferencia.

Ejercicio 4

1. Pon la ecuación \displaystyle{ \frac{4x^2}{9} + 25y^2 = 1 } en forma estándar.
2. ¿Cuál es el centro?
3. ¿Cuánto mide el eje mayor?
4. ¿Cuánto mide el eje menor?
5. Gráficalo.

Respuesta

Esto casi parece una elipse en forma estándar, ¿no? Incluso tiene un número en el lado derecho. Pero no lo es. No hay espacio en la forma estándar para los valores 4 y 25 en los numeradores. ¿Cómo podemos deshacernos de ellos para llegar a la forma estándar?

Reescribe el término de la izquierda, \displaystyle{\frac{4x^2}{9}, dividiendo la parte superior e inferior de la fracción entre 4. Deja la parte inferior como una fracción; no la conviertas en un decimal.

Reescribe el término de la derecha, 25y^2, como \displaystyle{\frac{25y^2}{1}, y divide la parte superior e inferior de la fracción entre 25. Deja la parte de abajo como una fracción; no la conviertas en un decimal.

La ecuación es ahora:

displaystyle{\begin{align} \frac{4x^2}{9} + 25y^2 &= 1 \frac{4x^2}{4}{frac{9}{4} + \frac{\frac{25y^2}{25}}{\frac{1}{25}} &= 1 \frac{x^2}{\frac{9}{4} + \frac{y^2}{\frac{1}{25} &= 1 \frac{{align}}

Desde la ecuación estándar, \displaystyle{\frac {\left(x-h\right)^2}{a^2}+\frac {\left(y-k\right)^2}{b^2}= 1}, sabemos que el centro está en \left(h,k\right). Como ambos son cero en esta ecuación, el centro está en \left(0,0\right).

El eje mayor depende de cuál es más largo, a o b. Resolvamos para ambos, y averigüemos cuál es mayor después.

\displaystyle{{begin{align} a^2 &= \frac{9}{4} \\ a &= \frac{3}{2} \\ 2a &= \frac{6}{2} &= 3 \N-end{align}

Displaystyle{\i} egin{align} b^2 &= \frac{1}{25} \\ b &= \frac{1}{5} \\ 2b &= \frac{2}{5} SaludSaludspan

Dado que \displaystyle{3>\frac{2}{5}, 2a>2b, y 2a es el eje mayor. La longitud del eje mayor es 2a = 3, y la longitud del eje menor es \displaystyle{2b = \frac{2}{5}.



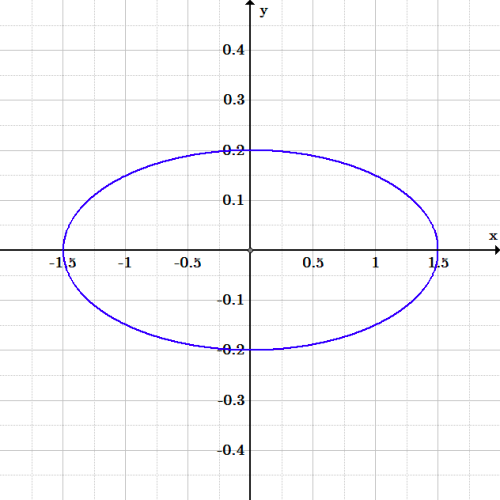
Ejercicio 4 elipse: Gráfica de la elipse \frac{4x^2}{9} + 25y^2 = 1.