Est-il possible pour nous de transformer une fonction en la rétrécissant ? Oui ! L’une des techniques de transformation les plus utiles que vous rencontrerez est la compression verticale.
La compression verticale nous aide à rétrécir les fonctions verticalement.
Mais de combien ? Cela dépend du facteur d’échelle.
Avant de commencer à plonger plus profondément dans ce sujet, assurons-nous que nous sommes équipés des bonnes techniques et connaissances passant en revue les sujets suivants :
- Comprendre les fonctions parentes communes que nous pourrions rencontrer.
- Rafraîchir vos connaissances sur les transformations verticales et horizontales.
- Apprendre à appliquer les étirements verticaux et horizontaux également.
Dans cet article, nous apprendrons à identifier les compressions verticales étant donné les expressions et les graphiques de deux fonctions ou plus. Nous appliquerons également nos connaissances sur les compressions verticales en représentant graphiquement différents types de fonctions.
Qu’est-ce qu’une compression verticale ?
Les compressions verticales se produisent lorsqu’une fonction est multipliée par un facteur d’échelle rationnel. La base du graphique de la fonction reste la même lorsqu’un graphique est compressé verticalement. Seules les valeurs de sortie seront affectées.
Pourquoi n’observons-nous pas ce qui se passe lorsque f(x) est compressée verticalement par un facteur d’échelle de 1/2 et 1/4 ?
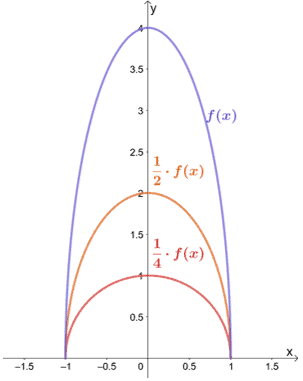
Comme nous pouvions nous y attendre, lorsque f(x) est compressée verticalement par un facteur de 1/2 et 1/4, le graphique est également compressé par le même facteur d’échelle.
En général, lorsqu’une fonction est compressée verticalement par a (où 0 < a < 1), le graphique se rétrécit du même facteur d’échelle. Appliquons le concept de manière à pouvoir comprimer f(x) = 6|x| + 8 par un facteur d’échelle de 1/2.
Pour comprimer f(x), nous allons multiplier la valeur de sortie par 1/2.
1/2 ∙ f(x) = 1/2 (6|x| + 8)
= 3|x| + 4
Maintenant, que se passe-t-il avec les coordonnées d’une fonction compressée par un facteur d’échelle de a, où 0 < a < 1 ? Si la fonction de base passe par le point (m, n), la fonction compressée verticalement passera par le point (m, an).
Comment compresser verticalement une fonction ? Nous avons maintenant compris comment la compression verticale affecte une fonction de base. Maintenant, comment appliquer cette technique lorsqu’on nous donne le graphique d’une fonction ?
Voici quelques-uns des concepts importants à retenir lorsque nous transformons des graphiques et les compressons verticalement :
- Seules les valeurs des coordonnées y changeront d’un facteur d’échelle de a (vérifiez si a est une fraction).
- Utilisez les points critiques et certaines paires ordonnées pour vous guider dans la compression d’un graphique.
- Retenez le ou les ordonnées en x du graphique mais l’ordonnée en y diminuera également d’un facteur d’échelle de a.
Pourquoi ne pas essayer de comprimer y = 4(x- 4) d’un facteur d’échelle de 1/4 ?
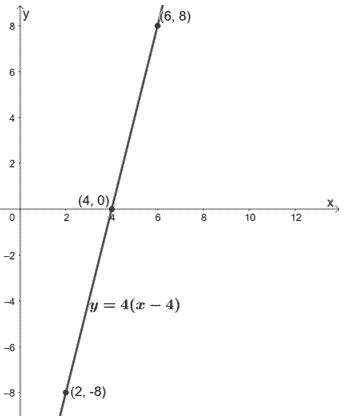
Comme nous l’avons mentionné, il est important de vérifier les points de référence et de s’assurer qu’ils peuvent être mis à l’échelle avec le bon facteur. Si nous voulons comprimer y = 4(x- 4) par un facteur d’échelle de 1/4, nous aurons les points suivants :
- (2, -8) → (2, -2)
- (6, 8) → (6, 2)
- L’ordonnée à l’origine en x, (4, 0), restera la même.
Une fois que nous avons certains des points pour le nouveau graphique compressé, graphions la fonction transformée.
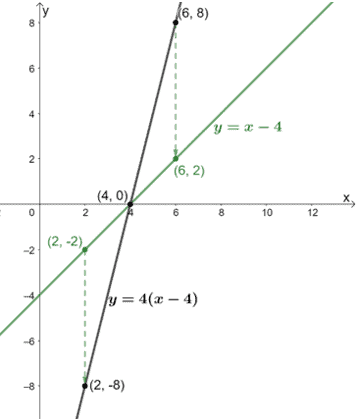
De ce fait, nous pouvons voir que lorsque y = 4(x – 4) est compressé par un facteur d’échelle de 1/4, la nouvelle fonction est égale à y = x – 4.
Nous pouvons appliquer le même processus lors de la compression verticale d’autres fonctions. Mais d’abord, pourquoi ne pas récapituler ce que nous avons appris jusqu’à présent avant d’essayer d’autres fonctions et graphiques ?
Résumé de la définition et des propriétés de la compression verticale
Voici quelques rappels importants lors de la compression verticale du graphique ou de l’expression d’une fonction donnée :
- Lorsque 0 < a < 1, af(x) renverra un graphique compressé verticalement avec un facteur d’échelle de a.
- Appliquez ce concept avec les coordonnées de la fonction, ainsi (m, n) devient (m, an).
- La valeur et la position de l’ordonnée à l’origine/s sont les mêmes.
- Lorsque f(x) est compressée verticalement, son domaine restera constant mais son étendue peut changer.
Nous sommes maintenant prêts à essayer d’autres exemples et à appliquer nos nouvelles connaissances sur les compressions verticales. N’oubliez pas de revoir vos notes !
Exemple 1
Le tableau des valeurs de f(x) est présenté ci-dessous. Si h(x) = 1/2 ∙ f(x), construisez un tableau de valeurs pour la fonction h(x).
| x | -3 | -2 | -..1 | 0 | 1 | 2 | 3 |
| f(x) | 20 | 10 | 4 | 2 | 4 | 10 | 20 |
Solution
(1, 2) → (1, 1)
Utiliser le même raisonnement pour compléter le reste du tableau de valeurs de h(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 10 | 5 | 2 | 1 | 2 | 5 | 10 |
Exemple 2
Utiliser le graphique présenté ci-dessous pour exprimer les relations entre les trois.
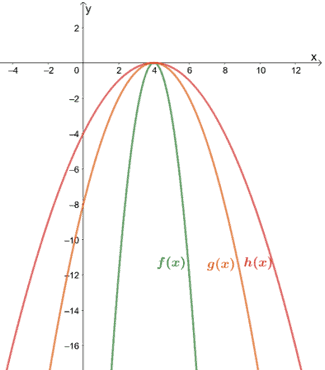
Solution
Nous pouvons aller de l’avant et vérifier quelques points de référence pour observer les compressions verticales effectuées sur chacun des graphiques.
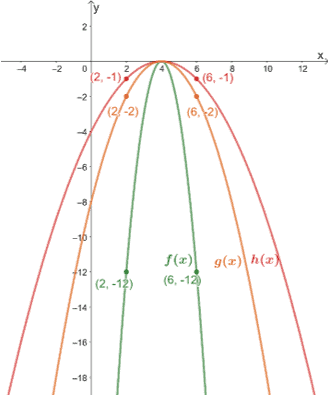
(2, -2) → (2, -12) et (6, -2) → (6, -12)
À partir des deux paires, nous pouvons voir que f(x) est le résultat lorsque g(x) est compressé verticalement par un facteur d’échelle de 1/6.
(2, -1) → (2, -2) et (6, -1) → (6, -2)
Donc, h(x) est le résultat lorsque g(x) est compressé verticalement par un facteur d’échelle de 1/2.
c. Observez les deux paires de points pour trouver le facteur d’échelle partagé entre f(x) et h(x).
(2, -1) → (2, -12) et (6, -1) → (6, -12)
De ce fait, on constate que h(x) est le résultat lorsque f(x) est compressé verticalement par un facteur d’échelle de 1/12.
Exemple 3
Graphiez la fonction mère de g(x) = 1/4 ∙ √x. Sur le même graphique, tracez g(x) en utilisant les compressions verticales.
Solution
Nous avons déjà appris que la fonction mère des fonctions racines carrées est y = √x. Allons-y et graphions d’abord y = √x.
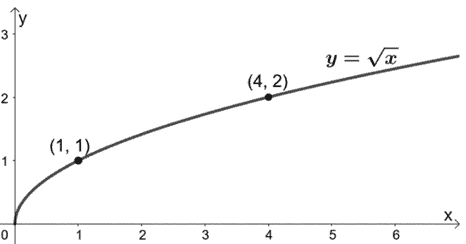
Nous avons ajouté quelques paires ordonnées comme guides une fois que nous graphions g(x). Comme nous voulons la comprimer verticalement, nous allons diviser les coordonnées y de la fonction mère par 4.
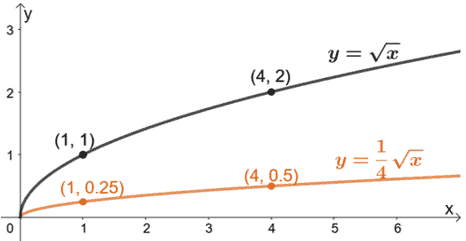
Donc, nous avons g(x) représentée par le graphique orange.
Exemple 4
Graphiez f(x) = 6 √(9 – x2) en trouvant ses ordonnées. Sur le même système de coordonnées, tracez le graphique de g(x) et h(x) étant donné les conditions suivantes :
- La fonction g(x) est le résultat de la compression verticale de f(x) par un facteur 1/2.
- La fonction h(x) est le résultat de g(x) étant compressée verticalement par un facteur de 1/3.
Solution
Comme suggéré, allons-y et trouvons les ordonnées x et y de f(x).
| x | -3 | 0 | 3 |
| f(x) | 0 | 18 | 0 |
Allons-y et traçons ces intercepts ainsi que le graphique de f(x).
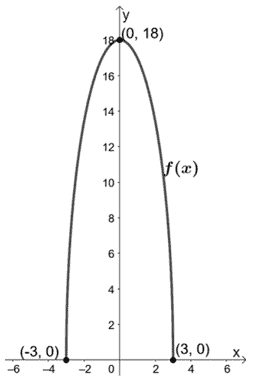
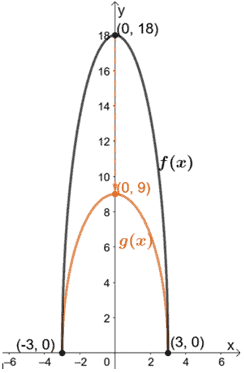
Poursuivons maintenant la représentation graphique de h(x) en mettant g(x) à l’échelle verticale de 1/3. Il en résulte que h(x) a un ordonnée à l’origine par (0, 3).
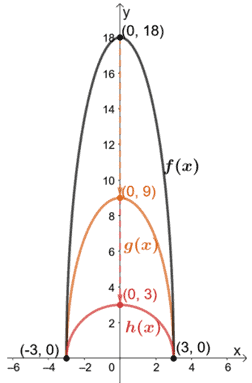
Nous avons maintenant les trois fonctions f(x), g(x) et h(x) sur un même système de coordonnées. Ce problème confirme également le fait que la base du graphique de la fonction et les ordonnées en x resteront les mêmes.
Exemple 5
Décrivez les transformations effectuées pour chaque paire de fonctions.
a. g(x) = 3×2 → h(x) = x2/15
b. g(x) = 12x + 4 → h(x) = 3x + 1
c. g(x) = 8|x – 2| – 4 → h(x) = |x -2| – 3
Solution
b. En divisant g(x) par 4, on obtient (12x + 4)/4 = 3x + 1, donc h(x) est le résultat de g(x) compressé verticalement par un facteur d’échelle de 1/4.
Questions pratiques
- Le tableau des valeurs de f(x) est présenté ci-dessous. Si h(x) = 1/3∙ f(x), construisez un tableau de valeurs pour la fonction h(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 30 | 15 | 6 | 3 | 6 | 15 | 30 |
2. Utilisez le graphique présenté ci-dessous pour exprimer les relations entre les trois.
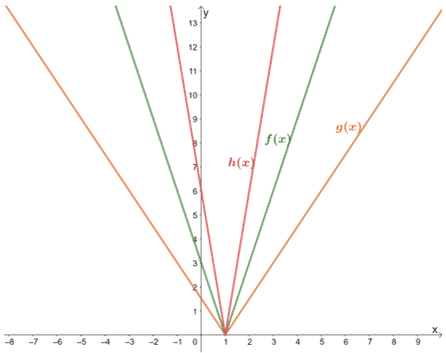
a. Quelle est la relation partagée entre g(x) et f(x) ?
b. Quelle est la relation partagée entre g(x) et h(x)?
c. Quelle est la relation partagée entre f(x) et h(x)?
3. Tracez le graphique de la fonction mère de g(x) = 1/3 ∙ x2. Sur le même graphique, tracez g(x) en utilisant les compressions verticales.
- La fonction g(x) est le résultat de f(x) compressée verticalement par un facteur 1/4.
- La fonction h(x) est le résultat de g(x) compressée verticalement par un facteur 1/2.
5. Décrivez les transformations effectuées pour chaque paire de fonctions.
a. g(x) = 2×2 → h(x) = x2/8
b. g(x) = 36x + 9 → h(x) = 4x + 1
c. g(x) = 6|x + 3| – 6 → h(x) = |x + 3| – 1