Extension verticale – Propriétés, graphique et exemples

Vous avez déjà remarqué des graphiques qui se ressemblent, mais dont l’un est plus étiré verticalement que l’autre ? Tout cela grâce à la technique de transformation que nous appelons l’étirement vertical.

L’étirement vertical sur un graphique va tirer le graphique original vers l’extérieur selon un facteur d’échelle donné.

Lorsqu’une fonction de base est multipliée par un certain facteur, nous pouvons immédiatement représenter graphiquement la nouvelle fonction en appliquant l’étirement vertical.

Avant de plonger plus profondément dans cette technique de transformation, il est préférable de réviser vos connaissances sur les sujets suivants :

• Comprendre les fonctions mères communes que nous pourrions rencontrer.
• Rafraîchir vos connaissances sur les transformations verticales et horizontales.

N’hésitez pas à cliquer sur les liens pour rafraîchir vos connaissances sur ces sujets essentiels. Nous allons maintenant aborder la troisième technique de transformation : l’étirement vertical.

Qu’est-ce qu’un étirement vertical ?

L’étirement vertical se produit lorsqu’un graphique de base est multiplié par un certain facteur supérieur à 1. Il en résulte que le graphique est tiré vers l’extérieur mais conserve les valeurs d’entrée (ou x). Lorsqu’une fonction est étirée verticalement, nous nous attendons à ce que les valeurs y de son graphique soient plus éloignées de l’axe des x.

Le graphique ci-dessous montre le graphique de f(x) et ses transformations. Pourquoi n’observons-nous pas comment f(x) se transforme lorsque nous multiplions les valeurs de sortie par un facteur de 3 et 6 ?

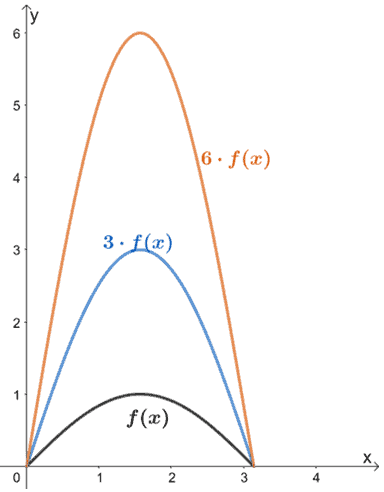
Lorsque f(x) est multiplié par des facteurs d’échelle de 3 et 6, son graphique s’étire selon les mêmes facteurs d’échelle. Nous pouvons également voir que leurs valeurs d’entrée (x pour ce cas) restent les mêmes ; seules les valeurs de y ont été affectées lorsque nous avons étiré f(x) verticalement.

Comment généraliser cette règle ? Lorsque nous avons |a| > 1, a – f(x) va étirer la fonction de base par un facteur d’échelle de a. Les valeurs d’entrée restent les mêmes, donc les points de coordonnées du graphique seront maintenant (x, ay).

Cela signifie que si f(x) = 5x + 1 est étirée verticalement par un facteur de 5, la nouvelle fonction sera équivalente à 5 – f(x). Par conséquent, la fonction résultante est 5(5x + 1) = 25x + 5.

Comment étirer verticalement une fonction?

Lorsqu’on nous donne le graphique d’une fonction, nous pouvons l’étirer verticalement en tirant la courbe vers l’extérieur en fonction du facteur d’échelle donné. Voici quelques éléments à retenir lorsque nous étirons verticalement des fonctions :

• Assurez-vous que les valeurs de x restent les mêmes, de sorte que la base de la courbe ne changera pas.
• Cela signifie que lorsque vous appliquez des étirements verticaux sur un graphique de base, ses ordonnées en x resteront les mêmes.
• Prenez note des nouveaux points critiques, comme le nouveau point maximal du graphique.

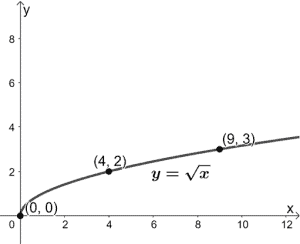
Pourquoi ne pas essayer d’étirer verticalement la fonction y = √x par un facteur 2 ?

Nous avons inclus des points de repère en soulignant comment ils changent également lorsque nous traçons le graphique de la nouvelle fonction y = 2√x. Qu’attendons-nous du nouveau graphique ?

Il commencera toujours à l’origine, les coordonnées y augmenteront d’un facteur 2 et le graphique s’étirera d’un facteur 2.

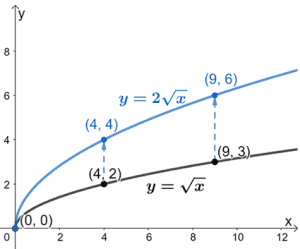
Le graphique ci-dessus montre comment nous pouvons étirer verticalement le graphique de y =√x par un facteur de 2 pour représenter également y = 2√x.

Nous pouvons appliquer le même processus lors de l’étirement vertical de différents types de fonctions et de graphiques. Avant d’essayer d’autres exemples, pourquoi ne pas résumer ce que nous avons appris jusqu’à présent sur l’étirement vertical ?

Résumé de la définition et des propriétés de l’étirement vertical

Nous avons maintenant appris l’effet de la mise à l’échelle d’une fonction par un facteur positif, a. Voici quelques indications importantes à retenir lorsque vous traitez des étirements verticaux sur des graphiques :

• Un étirement vertical ne se produit que lorsque le facteur d’échelle est supérieur à 1.
• Veillez à multiplier les coordonnées y par le même facteur d’échelle.
• Retenez la position des ordonnées en x.
• La fonction étirée verticalement aura le même domaine et une nouvelle étendue.

Gardons ces rappels utiles à l’esprit lorsque nous résoudrons les questions après cette section. Prêt ? Commençons à appliquer cette technique de transformation !

Exemple 1

La fonction, g(x), est obtenue en étirant verticalement f(x) = x2 + 1 par un facteur d’échelle de 3. Laquelle des expressions suivantes est la bonne expression pour g(x) ?

1. g(x) = 3×2 + 1
2. g(x) = x2 + 3
3. g(x) = 3×2 + 3
4. g(x) = 3(x + 1)2

Solution

Lorsque nous étirons une fonction verticalement, nous multiplions la fonction de base par son facteur d’échelle. Par conséquent, nous avons g(x) = 3 – f(x). Assurons-nous de distribuer 3 à chacun des termes de f(x).

g(x) = 3(x2 + 1)

=3×2 + 3

Ce qui signifie que l’expression correcte de g(x) est 3×2 + 3.

Exemple 2

Le tableau des valeurs de f(x) est présenté ci-dessous. Si g(x) = 4-f(x), construisez un tableau de valeurs pour la fonction g(x).

x	-6	-4	-2	2	4	6
f(x)	9	4	1	1	4	9

Solution

Puisque g(x) = 4-f(x), la fonction g(x) est étirée verticalement par un facteur d’échelle de 4. Qu’est-ce que cela signifie pour son tableau de valeurs ? 9 =

Nous multiplions chaque valeur de f(x) par 4 pour trouver les valeurs de sortie de g(x). Notez que les valeurs des coordonnées x resteront les mêmes.

x	-6	-4	-2	2	4	6
g(x)	36	16	4	4	16	36

Exemple 3

Remplir les blancs pour rendre vraies les affirmations suivantes, étant donné que f(x) = |x|.

1. Si g(x) = 4|x|, la fonction g(x) est étirée verticalement par un facteur d’échelle de ________.
2. Si le graphique de f(x) est étiré verticalement par un facteur 2 pour atteindre h(x), alors h(x) = ___ ∙ f(x).
3. Si le graphique de f(x) est étiré verticalement par un facteur 3, l’expression de h(x) est ________.

Solution

• Comparant g(x) et f(x), on a g(x) = 4 ∙ f(x). Cela signifie que la fonction g(x) est étirée verticalement par un facteur 4.
• Étirer f(x) verticalement par un facteur 2 aura pour conséquence que h(x) sera égal à 2 fois f(x).
• Etendre verticalement f(x) par un facteur 3 aura pour résultat que h(x) sera égal à 3 fois f(x). Par conséquent, h(x) = 3|x|.

Exemple 4

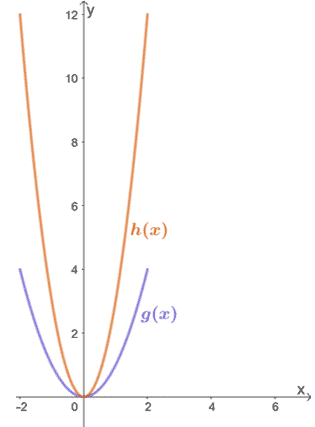
Observez les deux fonctions présentées ci-dessous et reliez h(x) à g(x).

Solution

Par simple inspection, on constate que h(x) résulte de l’étirement vertical de g(x). Pour trouver le facteur par lequel h(x) a été étiré, inspectons quelques valeurs correspondantes pour g(x) → h(x).

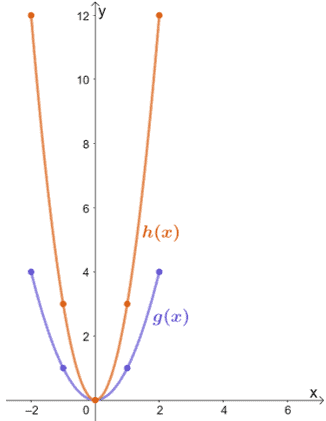
• (0, 0) → (0, 0)
• (1, 1) → (1, 3)
• (2, 4) → (1, 12)

Nous pouvons voir que la coordonnée y de h(x) est trois fois celle de g(x) pour chaque paire de points. Cela signifie que h(x) = 3 ∙ g(x), donc que h(x) est le résultat de l’étirement vertical de g(x) par un facteur d’échelle de 3.

Exemple 5

La fonction, A(x), modélise la distance (en km) parcourue par la voiture A sur une période de temps (en heures).

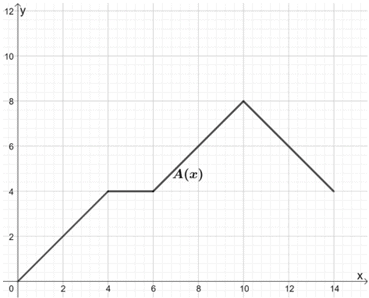
Jack veut comparer ce modèle à B(x), dont le mouvement suit le même schéma, mais la voiture observée peut parcourir deux fois la distance de A(x). Utilisez le graphique de A(x) pour esquisser le graphique de B(x).

Solution

Puisque B(x) = 2 ∙ A(x), on étire verticalement le graphique de A(x) par un facteur d’échelle de 2.

Pour ce faire, nous pouvons prendre note de certains points du graphique et trouver leurs valeurs correspondantes pour B(x). Pour trouver les nouvelles paires ordonnées, multiplions chaque coordonnée y par 2.

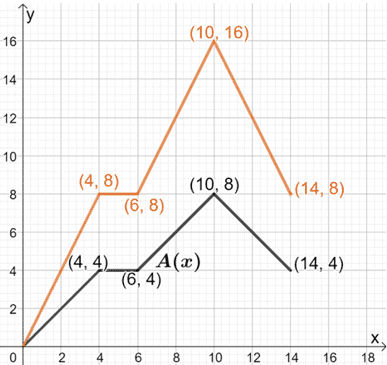
Nous pouvons relier ces points pour former B(x). Gardez à l’esprit que la forme de A(x) et de sa base doit rester la même.

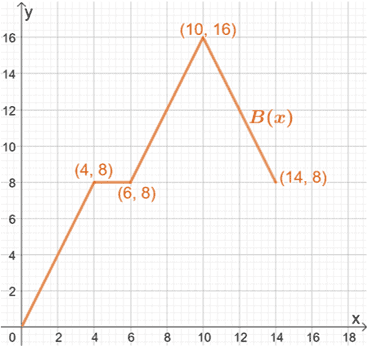
Hence, nous avons le graphique final pour B(x), comme indiqué ci-dessus.

Exemple 6

Observez les deux fonctions présentées ci-dessous et reliez h(x) à g(x). Quelle est l’expression de h(x)?

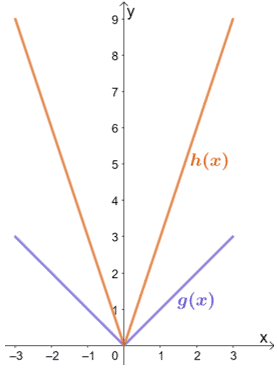
Solution

Nous pouvons voir que h(x) est le résultat de g(x) est étiré verticalement par un certain facteur d’échelle. Allons-y et inspectons certains des points correspondants.

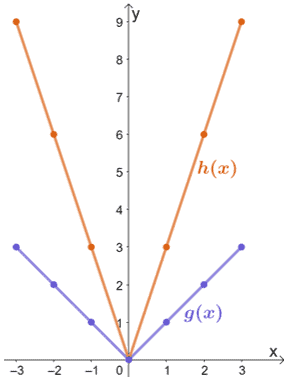
• (-3, 3) → (-3, 9)
• (-1, 1) → (-1, 3)
• (0, 0) → (0, 0)
• (1, 1) → (1, 3)
• (3, 3) → (3, 9)

À partir de là, nous pouvons voir que lorsque g(x) est étiré verticalement par un facteur d’échelle de 3, le graphique résultant sera celui de h(x). Par conséquent, nous avons h(x) = 3 ∙ g(x).

La fonction g(x) représente la fonction mère de toutes les fonctions à valeur absolue. Cela signifie que g(x) = |x|. Pour trouver l’expression de h(x), on multiplie l’expression de g(x) par 3. On a donc h(x) = 3|x|.

Exemple 7

Trouvez les transformations effectuées sur f(x) pour atteindre h(x).

1. f(x) = x2 → h(x) = 3×2 + 24x + 48
2. f(x) = √x → h(x) = 2√(x + 2)
3. f(x) = ex → h(x) = 5(ex – 2) – 1

.

Solution

• Essayons d’abord de factoriser l’expression de h(x) pour voir si nous pouvons trouver les transformations appliquées sur f(x). Commençons par factoriser h(x) :
  • h(x) = 3(x2 + 8x + 16) = 3(x + 4)2 = 3 ∙ f(x + 4)
  • À partir de cette forme factorisée, nous pouvons voir que h(x) est le résultat lorsque f(x) est translaté de 4 unités vers la gauche et étiré verticalement de 3.

Prenez note du facteur multiplié à √x et de l’unité soustraite de la valeur d’entrée.

• Il en résulte que h(x) = 2 ∙ f(x + 2).
• En conséquence, f(x) doit être translaté de 2 unités vers la gauche et étiré verticalement de 2.

Observons la différence entre ex et h(x).

• h(x) = 5 ∙ ex – 2 -1 , par conséquent, nous avons h(x) = 5 ∙ f(x – 2) – 1.
• Cela signifie que f(x) est translaté de 2 unités vers la droite, étiré verticalement de 5 et translaté d’une unité vers le bas.

Exemple 8

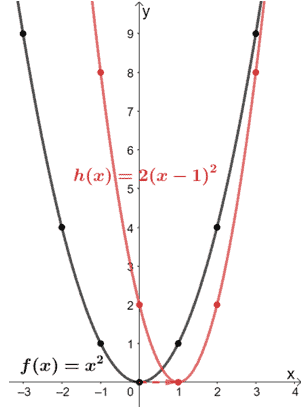
Quelles sont les transformations effectuées sur f(x) pour qu’il en résulte h(x) = 2×2 – 4x + 2 ? Utilisez le graphique de f(x) illustré ci-dessous pour vous guider. Appliquez les transformations au graphique h(x).

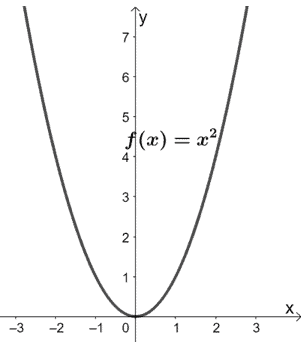
Solution

Essayons d’abord de factoriser l’expression de h(x) pour voir si nous pouvons trouver les transformations appliquées sur f(x).

Commencez par factoriser le facteur commun partagé par les trois termes.

2×2 – 4x + 2 = 2(x2 – 2x + 1)

Factoriser l’expression en utilisant (a – b)2 = a2 – 2ab + b2.

2(x2 – 2x + 1) = 2(x – 1)2

Donc, on a h(x) = 2(x – 1)2. À partir de cette forme, nous pouvons voir ce qui suit :

• Depuis (x – 1)2, nous pouvons voir que f(x) a été translaté d’une unité vers la droite.
• Le graphique résultant a ensuite été étiré verticalement par un facteur de 2.

Utilisons ces transformations et le graphique de f(x) pour tracer h(x). Commençons donc par translater la fonction mère y = x2 d’une unité vers la droite.

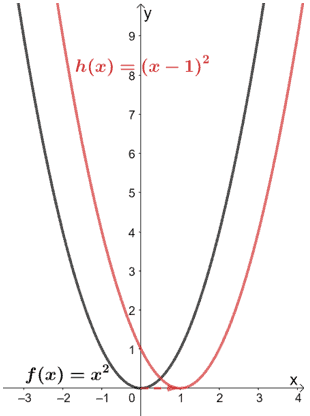
Maintenant, étirons le graphique verticalement par un facteur d’échelle de deux.

Sortons la fonction de référence et retournons le graphique final de h(x).

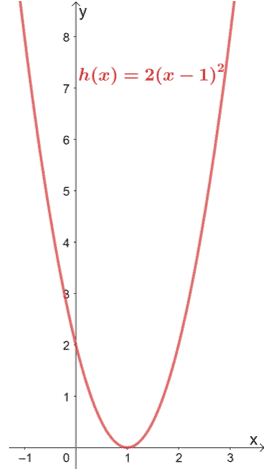
Cet exemple montre comment les transformations peuvent faire gagner du temps lors de la représentation graphique de familles de fonctions.

Questions pratiques

1. La fonction, g(x), est obtenue en étirant verticalement f(x) = 3×3 + 2 par un facteur d’échelle de 4. Laquelle des expressions suivantes est la bonne pour g(x) ?
a. g(x) = 3×3 + 8
b. g(x) = 3×3 + 6
c. g(x) = 12×3 + 2
d. g(x) = 12×3 + 8

2. La table des valeurs de f(x) est présentée ci-dessous. Si g(x) = 3-f(x), construisez un tableau de valeurs pour la fonction g(x).

x	-3	-2	-1	0	1	2	3
f(x)	-27	-8	-1	0	1	8	27

3. Remplissez les espaces vides pour que les affirmations suivantes soient vraies, étant donné que f(x) = √x.
a. Si g(x) = 5√x, la fonction g(x) est étirée verticalement par un facteur d’échelle de ________.
b. Si le graphique de f(x) est étiré verticalement par un facteur 4 pour atteindre h(x), alors h(x) = ___ ∙ f(x).
c. Si le graphique de f(x) est étiré verticalement par un facteur 2, l’expression de h(x) est ________.

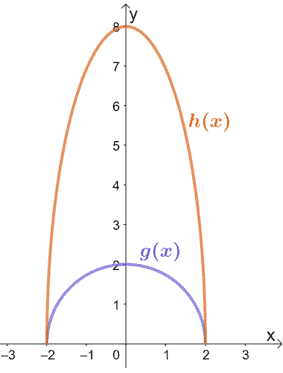
4. Observez les deux fonctions présentées ci-dessous et reliez h(x) à g(x). Si g(x) = √(4 – x2), quelle est l’expression de h(x) ?

5. La fonction, A(x), modélise la distance (en km) parcourue par la voiture A au cours du temps (en heures).

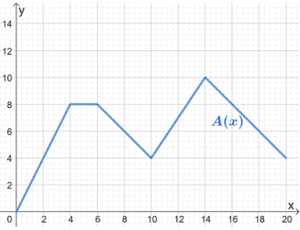
Mary veut comparer ce modèle à B(x), dont le mouvement suit le même schéma, mais la voiture observée peut parcourir trois fois la distance de A(x). Utilisez le graphique de A(x) pour esquisser le graphique de B(x).

6. Quelles sont les transformations effectuées sur f(x) pour qu’il en résulte h(x) = 5x + 6 ? Utilisez le fait que f(x) est la fonction mère de toutes les fonctions linéaires. Appliquez les transformations pour tracer le graphique de h(x).

7. Trouvez les transformations effectuées pour chaque paire de fonctions et tracez le graphique de h(x) pour chaque cas.

a. g(x) = x2 → h(x) = 5×2 – 20x + 20

b. g(x) = √x → h(x) = 3√(x – 1)

c. g(x) = 2x → h(x) = 3(2x – 2) + 6

Les images/dessins mathématiques sont créés avec GeoGebra.