¿Es posible que transformemos una función reduciéndola? ¡¡¡Sí!!! Una de las técnicas de transformación más útiles que encontrarás es la compresión vertical.
La compresión vertical nos ayuda a encoger las funciones verticalmente.
¿Pero en cuánto? Depende del factor de escala.
Antes de empezar a profundizar en este tema, vamos a asegurarnos de que estamos equipados con las técnicas y conocimientos adecuados repasando los siguientes temas:
- Entender las funciones padre más comunes que podemos encontrar.
- Refrescar los conocimientos sobre las transformaciones verticales y horizontales.
- Aprender a aplicar los estiramientos verticales y horizontales también.
- Sólo los valores de las coordenadas y cambiarán en un factor de escala de a (comprueba si a es una fracción).
- Usa los puntos críticos y algunos pares ordenados para guiarte en la compresión de una gráfica.
- Mantén la/s intersección/es de la gráfica pero la intersección y también disminuirá en un factor de escala a.
- (2, -8) → (2, -2)
- (6, 8) → (6, 2)
- La intersección x, (4, 0), seguirá siendo la misma.
- Cuando 0 < a < 1, af(x) devolverá una gráfica comprimida verticalmente con un factor de escala de a.
- Aplica este concepto con la coordenada de la función, por lo que (m, n) se convierte en (m, an).
- El valor y la posición de la/s intersección/es de x son los mismos.
- Cuando f(x) se comprime verticalmente, su dominio permanecerá constante pero su rango puede cambiar.
- La función g(x) es el resultado de que f(x) se comprima verticalmente por un factor de 1/2.
- La función h(x) es el resultado de que g(x) esté comprimida verticalmente por un factor de 1/3.
En este artículo, aprenderemos a identificar las compresiones verticales dadas las expresiones y gráficas de dos o más funciones. También aplicaremos nuestros conocimientos sobre compresiones verticales graficando diferentes tipos de funciones.
¿Qué es una compresión vertical?
Las compresiones verticales se producen cuando una función se multiplica por un factor de escala racional. La base de la gráfica de la función sigue siendo la misma cuando una gráfica se comprime verticalmente. Sólo los valores de salida se verán afectados.
¿Por qué no observamos lo que ocurre cuando f(x) se comprime verticalmente por un factor de escala de 1/2 y 1/4?
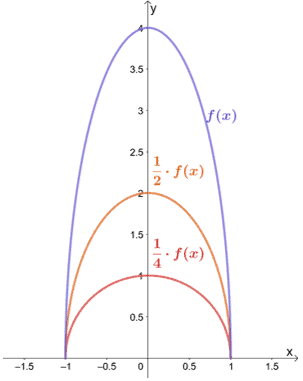
Como podíamos esperar, cuando f(x) se comprime verticalmente por un factor de 1/2 y 1/4, la gráfica también se comprime por el mismo factor de escala.
En general, cuando una función se comprime verticalmente por a (donde 0 < a < 1), la gráfica se comprime por el mismo factor de escala. Apliquemos el concepto para que podamos comprimir f(x) = 6|x| + 8 por un factor de escala de 1/2.
Para comprimir f(x), multiplicaremos el valor de salida por 1/2.
1/2 ∙ f(x) = 1/2 (6|x| + 8)
= 3|x| + 4
Ahora, ¿qué ocurre con las coordenadas de una función comprimida por un factor de escala a, donde 0 < a < 1? Si la función base pasa por el punto (m, n), la función comprimida verticalmente pasará por el punto (m, an).
¿Cómo comprimir verticalmente una función? Ya hemos entendido cómo afecta la compresión vertical a una función base. Ahora, ¿cómo aplicamos esta técnica cuando nos dan la gráfica de una función?
Aquí tienes algunos de los conceptos importantes que debes recordar cuando transformamos gráficas y las comprimimos verticalmente:
¿Por qué no probamos a comprimir y = 4(x- 4) en un factor de escala 1/4?
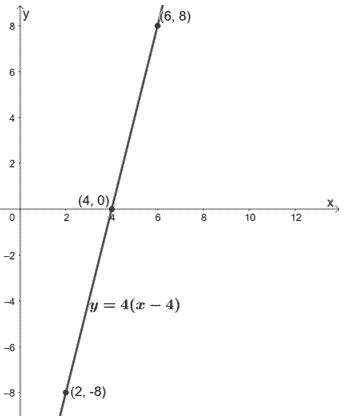
Como hemos comentado, es importante comprobar los puntos de referencia y asegurarse de que se pueden escalar con el factor adecuado. Si queremos comprimir y = 4(x- 4) con un factor de escala de 1/4, tendremos los siguientes puntos:
Una vez que tenemos algunos de los puntos para la nueva gráfica comprimida, vamos a graficar la función transformada.
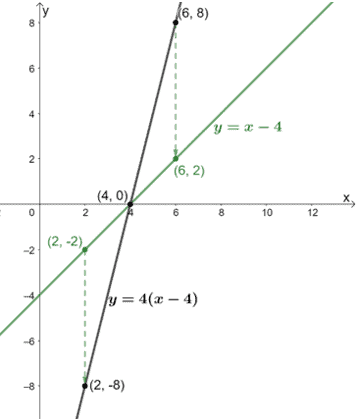
A partir de esto, podemos ver que cuando y = 4(x – 4) se comprime con un factor de escala de 1/4, la nueva función es igual a y = x – 4.
Podemos aplicar el mismo proceso al comprimir verticalmente otras funciones. Pero primero, ¿por qué no recapitulamos lo que hemos aprendido hasta ahora antes de probar con otras funciones y gráficas?
Resumen de la definición y propiedades de la compresión vertical
Aquí tienes algunos recordatorios importantes a la hora de comprimir verticalmente la gráfica de una determinada función o expresión:
Ya estamos preparados para probar más ejemplos y aplicar nuestros nuevos conocimientos sobre compresiones verticales. No olvides repasar tus apuntes!
Ejemplo 1
A continuación se muestra la tabla de valores de f(x). Si h(x) = 1/2 ∙ f(x), construye una tabla de valores para la función h(x).
| x/td> | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 20 | 10 | 4 | 2 | 4 | 10 | 20 |
Solución
(1, 2) → (1, 1)
Usa el mismo razonamiento para completar el resto de la tabla de valores de h(x).
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
| f(x) | 10 | 5 | 2 | 2 | 5 | 10 |
Ejemplo 2
Usa el gráfico que se muestra a continuación para expresar las relaciones entre los tres.
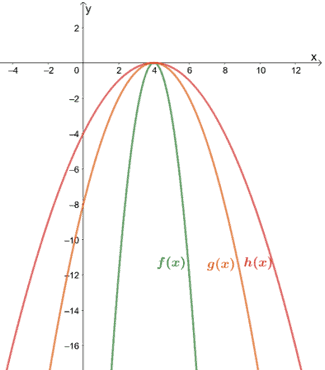
Solución
Podemos pasar a comprobar algunos puntos de referencia para observar las compresiones verticales realizadas en cada una de las gráficas.
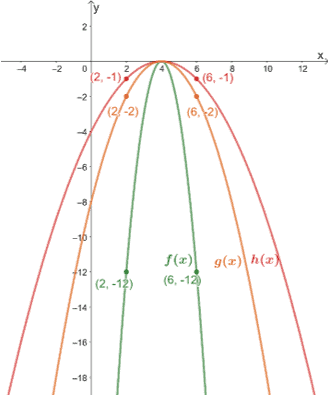
(2, -2) → (2, -12) y (6, -2) → (6, -12)
A partir de los dos pares, podemos ver que f(x) es el resultado cuando g(x) se comprime verticalmente por un factor de escala de 1/6.
(2, -1) → (2, -2) y (6, -1) → (6, -2)
Por tanto, h(x) es el resultado cuando g(x) se comprime verticalmente por un factor de escala de 1/2.
c. Observa los dos pares de puntos para encontrar el factor de escala compartido entre f(x) y h(x).
(2, -1) → (2, -12) y (6, -1) → (6, -12)
A partir de esto, podemos ver que h(x) es el resultado cuando f(x) se comprime verticalmente por un factor de escala de 1/12.
Ejemplo 3
Grafíe la función madre de g(x) = 1/4 ∙ √x. En la misma gráfica, grafica g(x) usando compresiones verticales.
Solución
Ya hemos aprendido que la función madre de las funciones de raíz cuadrada es y = √x. Sigamos adelante y grafiquemos primero y = √x.
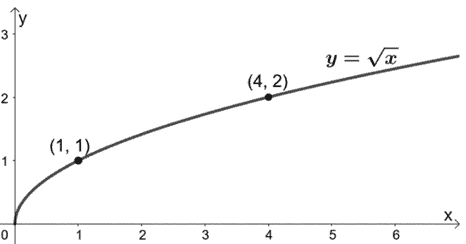
Hemos añadido algunos pares ordenados como guías una vez que grafiquemos g(x). Como queremos comprimirla verticalmente, dividiremos las coordenadas y de la función padre entre 4.
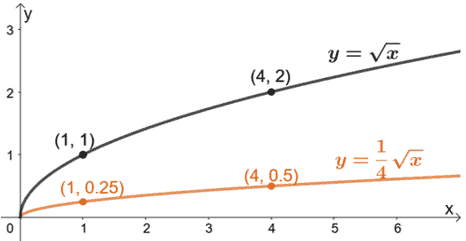
Así, tenemos g(x) representada por la gráfica naranja.
Ejemplo 4
Grafía f(x) = 6 √(9 – x2) encontrando sus interceptos. En el mismo sistema de coordenadas, grafica g(x) y h(x) dadas las siguientes condiciones:
Solución
Como se ha sugerido, vamos a encontrar las intersecciones x e y de f(x).
| x | -3 | 0 | 3 |
| f(x) | 0 | 18 | 0 |
Vamos a trazar estos interceptos así como la gráfica de f(x).
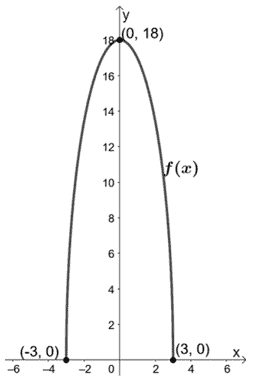
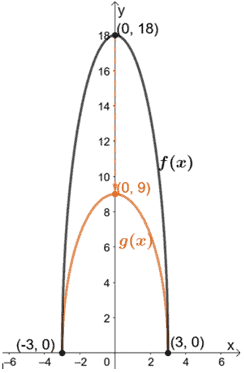
Continuemos ahora graficando h(x) escalando g(x) verticalmente en 1/3. Esto da como resultado que h(x) tiene una intersección y en (0, 3).
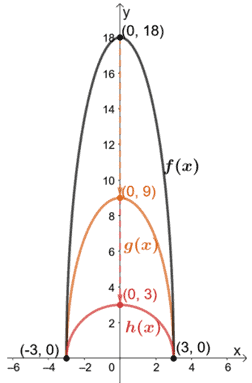
Ahora tenemos las tres funciones f(x), g(x) y h(x) en un sistema de coordenadas. Este problema también confirma el hecho de que la base de la gráfica de la función y las intersecciones de x seguirán siendo las mismas.
Ejemplo 5
Describe las transformaciones realizadas para cada par de funciones.
a. g(x) = 3×2 → h(x) = x2/15
b. g(x) = 12x + 4 → h(x) = 3x + 1
c. g(x) = 8|x – 2| – 4 → h(x) = |x -2| – 3
Solución
b. Dividiendo g(x) entre 4 resultará (12x + 4)/4 = 3x + 1, por lo que h(x) es el resultado de que g(x) se comprima verticalmente por un factor de escala de 1/4.
Preguntas de práctica
- La tabla de valores de f(x) se muestra a continuación. Si h(x) = 1/3∙ f(x), construye una tabla de valores para la función h(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 30 | 15 | 6 | 3 | 6 | 15 |
2. Utiliza el gráfico que se muestra a continuación para expresar las relaciones entre los tres.
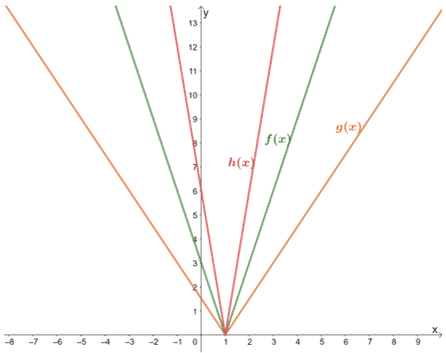
a. ¿Cuál es la relación que comparten g(x) y f(x)?
b. ¿Cuál es la relación que comparten g(x) y h(x)?
c. ¿Cuál es la relación que comparten f(x) y h(x)?
3. Grafica la función madre de g(x) = 1/3 ∙ x2. En la misma gráfica, grafique g(x) utilizando compresiones verticales.
- La función g(x) es el resultado de que f(x) se comprima verticalmente en un factor de 1/4.
- La función h(x) es el resultado de que g(x) se comprima verticalmente en un factor de 1/2.
5. Describe las transformaciones realizadas para cada par de funciones.
a. g(x) = 2×2 → h(x) = x2/8
b. g(x) = 36x + 9 → h(x) = 4x + 1
c. g(x) = 6|x + 3| – 6 → h(x) = |x + 3| – 1